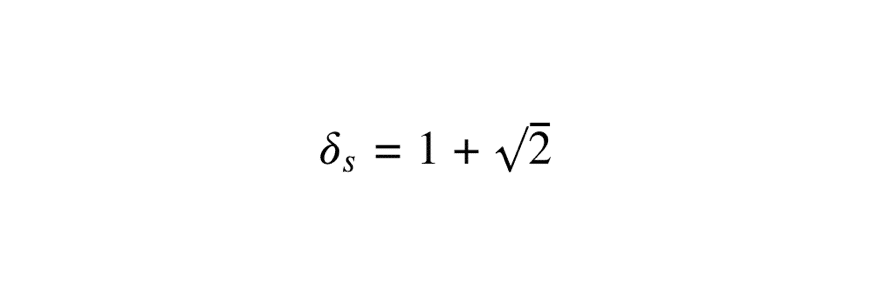En mathématiques, certains nombres transcendent leur simple valeur numérique pour devenir des symboles de beauté et d’harmonie. Le nombre d’or, avec ses nombreuses apparitions en art, en architecture et en nature, est probablement le plus célèbre de ces nombres. Cependant, il existe un autre nombre, moins connu mais tout aussi fascinant : le nombre d’argent. Ce dernier, noté \( \delta_s \), émerge dans des contextes similaires à ceux du nombre d’or, notamment dans les suites récurrentes, les constructions géométriques et les fractions continues. Cet article te propose d’explorer en profondeur les propriétés mathématiques du nombre d’argent, ses liens avec d’autres nombres célèbres et son rôle dans divers domaines mathématiques. Que tu connaisses ces concepts ou que tu les découvres pour la première fois, tu trouveras ici une exploration détaillée de ce nombre remarquable. Ce nombre reste lié d’une manière ou d’une autre à la fameuse suite de Fibonacci.
Le nombre d’argent
Le nombre d’argent est une constante mathématique moins connue que son célèbre cousin, le nombre d’or, mais tout aussi fascinante. Il est souvent rencontré dans des contextes liés aux suites récurrentes et aux proportions géométriques. Tout comme le nombre d’or, le nombre d’argent possède des propriétés remarquables et apparaît dans divers domaines des mathématiques, y compris l’algèbre, la géométrie et les mathématiques discrètes.
Le nombre d’argent, souvent noté \( \delta_s \) ou \( \lambda \), est défini comme la solution positive de l’équation quadratique suivante :
\[
x^2 = 2x + 1
\]
Résolvons cette équation pour mieux comprendre ce nombre.
Résolution de l’équation quadratique
L’équation caractéristique du nombre d’argent est donnée par :
\[
x^2 – 2x – 1 = 0
\]
Ainsi, nous avons :
\[
x = \frac{2 \pm \sqrt{(-2)^2 – 4(1)(-1)}}{2(1)} = \frac{2 \pm \sqrt{4 + 4}}{2} = \frac{2 \pm \sqrt{8}}{2} = \frac{2 \pm 2\sqrt{2}}{2}
\]
Cela simplifie à :
\[
x = 1 \pm \sqrt{2}
\]
Étant donné que nous cherchons la solution positive, le nombre d’argent est :
\[
\delta_s = 1 + \sqrt{2} \approx 2.414
\]
Propriétés du nombre d’argent
Le nombre d’argent partage plusieurs propriétés intéressantes avec le nombre d’or. Explorons quelques-unes de ces propriétés.
Lien avec les suites de Pell
Le nombre d’argent, \( \delta_s = 1 + \sqrt{2}, \) est intimement lié à la suite de Pell, une suite récurrente définie par la relation :
\[
P_{n+2} = 2P_{n+1} + P_n
\]
avec des conditions initiales \( P_0 = 0 \) et \( P_1 = 1. \) Cette relation récurrente produit une suite de nombres qui, comme la suite de Fibonacci pour le nombre d’or, tend vers une limite particulière : le nombre d’argent. Le terme général de la suite de Pell peut être formulé grâce à une expression semblable à la formule de Binet pour Fibonacci :
\[
P_n = \frac{\varphi_2^n – \varphi_2’^n}{\varphi_2 – \varphi_2′}
\]
où \( \varphi_2 = 1 + \sqrt{2} \) et \( \varphi_2′ = 1 – \sqrt{2} \) sont les racines de l’équation quadratique \( x^2 = 2x + 1 \), caractérisant le nombre d’argent. Une des propriétés fascinantes de cette suite est que le rapport des termes successifs \( \displaystyle \frac{P_{n+1}}{P_n} \) se rapproche asymptotiquement du nombre d’argent à mesure que \( n \) devient très grand :
\[
\lim_{n \to \infty} \frac{P_{n+1}}{P_n} = \delta_s = 1 + \sqrt{2}
\]
En plus de la suite de Pell, la suite de Pell-Lucas, qui suit une relation récurrente similaire, renforce ce lien. Par conséquent, le nombre d’argent se manifeste naturellement comme la limite de ces rapports, soulignant son rôle central dans l’analyse des suites récurrentes de type Pell. Cette connexion reflète une structure mathématique profonde, similaire à celle qui lie le nombre d’or à la suite de Fibonacci.
Une identité algébrique
Une autre propriété remarquable du nombre d’argent est son identité algébrique simple qui le caractérise :
\[
\delta_s^2 = 2\delta_s + 1
\]
Cette identité peut être dérivée directement de l’équation quadratique originale. Ce qui est fascinant, c’est que cette propriété est très similaire à celle du nombre d’or, qui satisfait l’identité \( \varphi^2 = \varphi + 1. \)
Développement en fraction continue
Le nombre d’argent a un développement en fraction continue simple et élégant. Il peut être exprimé sous la forme :
\[ \delta_s = 2 + \frac{1}{2 + \frac{1}{2 + \frac{1}{2 + \frac{1}{2 + \dots}}}} \]
Cette fraction continue révèle la structure autosimilaire du nombre d’argent, un peu comme la fraction continue pour le nombre d’or \( \displaystyle \varphi = 1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \dots}}}} \).
La famille des nombres métalliques
Le nombre d’argent fait partie d’une famille plus large de constantes mathématiques appelées les nombres métalliques. Ces nombres, qui incluent également le célèbre nombre d’or, sont définis par une formule générale qui relie chacun d’eux à une suite récurrente spécifique. Un nombre métallique \( M_n \) est défini comme la solution positive de l’équation quadratique :
\[
x^2 = nx + 1
\]
où \( n \) est un entier positif. Par exemple, pour \( n = 1 \), nous obtenons le nombre d’or \( \displaystyle \varphi = \frac{1 + \sqrt{5}}{2} \), tandis que pour \( n = 2 \), nous obtenons le nombre d’argent \( \displaystyle \delta_s = 1 + \sqrt{2}. \) Chaque nombre métallique est associé à des propriétés géométriques et algébriques uniques, mais ils partagent tous cette relation fondamentale.
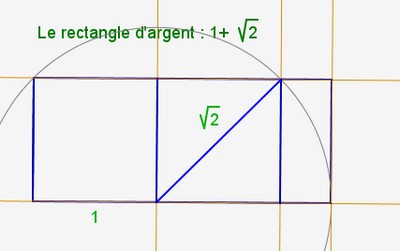
Le rectangle d’argent
Le rectangle d’argent est une figure géométrique caractérisée par un rapport entre sa longueur \( L \) et sa largeur \( W \) égal au nombre d’argent \( \delta_s = 1 + \sqrt{2} \). Ce rapport confère au rectangle une propriété d’autosimilarité. Si l’on soustrait un carré de côté \( W \) de ce rectangle, la figure restante est elle-même un rectangle d’argent. Mathématiquement, pour un rectangle d’argent, on a :
\[
\frac{L}{W} = \delta_s
\]
et après avoir enlevé un carré, le nouveau rectangle conserve ce rapport. Cette propriété, qui rappelle celle du rectangle d’or, montre comment le nombre d’argent se manifeste naturellement dans certaines constructions géométriques.
Comparaison avec le nombre d’or
Bien que le nombre d’or \( \varphi \) soit souvent plus célèbre, le nombre d’argent \( \delta_s \) présente des similitudes frappantes avec lui. Par exemple, tout comme \( \varphi \) est la solution positive de l’équation \( x^2 = x + 1 \), \( \delta_s \) est la solution de l’équation \( x^2 = 2x + 1. \) Ces deux nombres partagent une structure algébrique similaire, mais se distinguent par les contextes géométriques et numériques dans lesquels ils apparaissent.
Propriétés comparatives
- Équation quadratique : \( \varphi^2 = \varphi + 1 \) pour le nombre d’or et \( \delta_s^2 = 2\delta_s + 1 \) pour le nombre d’argent.
- Suite associée : suite de Fibonacci pour \( \varphi \) et suite de Pell pour \( \delta_s \).
- Fraction continue : \( \displaystyle \varphi = 1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \dots}}}} \). contre \( \delta_s = 2 + \frac{1}{2 + \frac{1}{2 + \frac{1}{2 + \frac{1}{2 + \dots}}}}. \)
Ces comparaisons montrent comment les deux nombres, bien que différents, se retrouvent dans des constructions mathématiques parallèles.
Aller plus loin sur le nombre d’argent
Le nombre d’argent est à l’origine de nombreuses recherches et nombreux problèmes mathématiques. Pour y voir plus clair, voici une cartographie de l’ensemble des recherches tournant autour (et de la suite de Fibonacci) :
| Tableau de correspondances suites/nombres (en lien avec Fibonacci/nombres métalliques) |
|
| Suites | Nombres |
| Suite de Fibonacci | Nombre d’or |
| Suite de Pell | Nombre d’argent |
| Généralisation de Fibonacci : les suites k-bonacci | Nombres métalliques : généralisation du nombre d’or |
| Suite de Lucas | Nombre de Lucas |
| Suite de Padovan | Nombre plastique |
| Suite de Perrin | Nombres pseudo-premiers de Perrin |
| Suite de Jacobsthal | Nombres oblongs de Jacobsthal |
| Polynôme/suite de Narayana | Nombre de Narayana |
| Nombre de Gildas | |
| Nombre de Keith | |
| Super nombre d’or | |
Conclusion
Le nombre d’argent, bien que moins connu que le nombre d’or, est un nombre avec une beauté mathématique unique. Il apparaît naturellement dans des suites récurrentes, des fractions continues et des formes géométriques. Pour les étudiants en classes préparatoires, comprendre ce nombre offre un aperçu précieux des connexions entre l’algèbre, la géométrie et la théorie des nombres.
Ainsi, bien que le nombre d’argent soit hors programme, la compréhension approfondie des propriétés liées à ce nombre permet de s’améliorer en analyse et en algèbre. L’étude de cette notion est un bon moyen de se préparer pour les épreuves écrites et orales. Pour t’entraîner sur cette notion, tu peux réaliser les sujets suivants : Ecricome 2018 (mathématiques approfondies) et la première Question Sans Préparation des Oraux HEC 2023.
Tu peux retrouver le méga-répertoire qui contient toutes les annales de concours et les corrigés ! Tu peux également accéder à toutes nos autres ressources mathématiques !