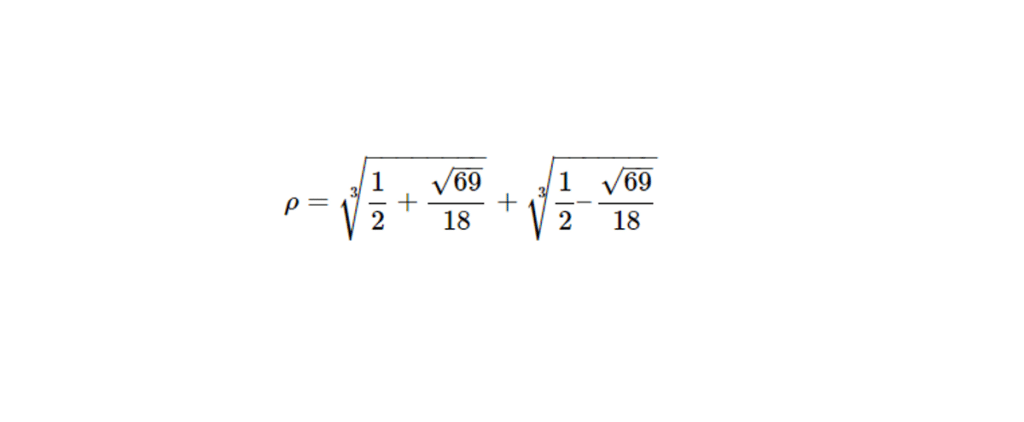Le nombre plastique, noté \(\rho\), est un nombre irrationnel fascinant qui se distingue par sa définition comme solution positive unique de l’équation cubique. Découvert par Hans van der Laan, ce nombre présente des propriétés mathématiques uniques, à la croisée de l’algèbre et de la géométrie. Moins connu que le nombre d’or, \(\rho\) offre une complexité et une richesse théorique qui en font un sujet d’étude captivant en mathématiques. Cet article explore les différentes propriétés algébriques et géométriques du nombre plastique, soulignant son importance et son intérêt dans l’étude des suites récurrentes et des structures géométriques. Ce nombre reste lié d’une manière ou d’une autre à la fameuse suite de Fibonacci.
Introduction au nombre plastique
Le nombre plastique, noté \(\rho\), est un nombre irrationnel qui occupe une place particulière en mathématiques en raison de sa relation avec une équation cubique simple, mais non triviale. Découvert par le mathématicien néerlandais Dom Hans van der Laan, ce nombre est la solution positive unique de l’équation suivante :
\[
x^3 = x + 1
\]
Définition et valeur du nombre plastique
Le nombre plastique est défini comme la solution positive de l’équation cubique :
\[
x^3 – x – 1 = 0
\]
Pour obtenir cette solution, on peut utiliser la méthode de Cardan, une technique classique pour résoudre les équations cubiques. Selon cette méthode, la solution pour \(x\) peut s’écrire sous la forme :
\[
\rho = \sqrt[3]{\frac{1}{2} + \frac{\sqrt{69}}{18}} + \sqrt[3]{\frac{1}{2} – \frac{\sqrt{69}}{18}}
\]
Cette expression, bien qu’exacte, est souvent approximée numériquement, donnant une valeur approchée pour \(\rho\) :
\[
\rho \approx 1,3247
\]
Contrairement aux solutions d’équations quadratiques qui sont souvent simples à manipuler, le nombre plastique est le fruit de la résolution d’une équation cubique, ce qui implique des propriétés et des comportements plus complexes.
Démonstration de l’unicité et de la positivité de la solution
Pour montrer que l’équation \(x^3 = x + 1\) admet une solution réelle unique et positive, considérons la fonction \(f(x) = x^3 – x – 1\), et cherchons les points où \(f(x) = 0\).
Calculons la dérivée de \(f(x)\) pour examiner sa monotonicité :
\[
f'(x) = 3x^2 – 1
\]
Les solutions de \(f'(x) = 0\) sont \(x = \pm \frac{1}{\sqrt{3}}\). Ainsi, la fonction dérivée \(f'(x)\) est négative pour \( \displaystyle -\frac{1}{\sqrt{3}} < x < \frac{1}{\sqrt{3}}\), et positive en dehors de cet intervalle.
Cela signifie que la fonction \(f(x)\) décroît sur \( \displaystyle \left]-\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\right[\) et croît sur \( \displaystyle \left]-\infty, -\frac{1}{\sqrt{3}}\right[\) et \( \displaystyle \left]\frac{1}{\sqrt{3}}, +\infty\right[\).
Calculons maintenant les valeurs de \(f(x)\) aux points critiques et à l’infini :
– \( \displaystyle f\left(-\frac{1}{\sqrt{3}}\right)\) et \( \displaystyle f\left(\frac{1}{\sqrt{3}}\right)\) sont tous deux strictement négatifs, ce qui signifie qu’il n’y a pas de valeurs où \(f(x) = 0\) dans \( \displaystyle \left[\frac{-1}{\sqrt{3}},\frac{1}{\sqrt{3}}\right]\).
– Comme \(f(x)\) tend vers \(-\infty\) lorsque \(x\) tend vers \(-\infty\), tend vers \(+\infty\) lorsque \(x\) tend vers \(+\infty\) et comme \( \displaystyle f(\frac{1}{\sqrt{3}})<0\) et \(f\) est strictement croissante sur \( \displaystyle \left[\frac{1}{\sqrt{3}},+\infty\right[,\) la fonction doit croiser l’axe des abscisses exactement une fois pour \(x > 0\).
En conséquence, l’équation \(f(x) = 0\) admet une unique solution positive, ce qui correspond au nombre plastique \(\rho.\) Cette solution est donc unique et positive, confirmant que \(\rho\) est bien défini.
Expression du nombre plastique comme itération infinie de racines cubiques
Le nombre plastique \(\rho\) peut être exprimé sous forme d’une itération infinie de racines cubiques imbriquées, ce qui est une autre manière élégante de représenter ce nombre. Cette expression découle directement de l’équation cubique \(x^3 = x + 1\), que \(\rho\) satisfait. Plus précisément, \(\rho\) peut être écrit comme suit :
\[
\rho = \sqrt[3]{1 + \sqrt[3]{1 + \sqrt[3]{1 + \sqrt[3]{1 + \cdots}}}}
\]
Pour comprendre pourquoi cette expression est correcte, considérons la relation d’itération associée à l’équation cubique. Partons de l’équation \(x^3 = x + 1,\), nous n’avons pas une équivalence mais nous savons que cela implique que \( \displaystyle x = \sqrt[3]{1 + x}\), ce qui nous conduit à examiner :
En substituant cette expression dans l’équation d’origine, nous obtenons par itération :
\[
x = \sqrt[3]{1 + \sqrt[3]{1 + \sqrt[3]{1 + \cdots}}}
\]
Cette forme montre que \(\rho\) peut être approché en itérant cette racine cubique de manière infinie. En pratique, cela signifie que chaque étape de l’itération se rapproche de plus en plus de la valeur exacte du nombre plastique. Cette représentation est non seulement mathématiquement correcte, mais aussi esthétiquement intrigante, car elle met en lumière la structure récursive sous-jacente au nombre plastique, illustrant la complexité de ce nombre irrationnel.
Propriétés géométriques et combinatoires du nombre plastique
En plus de ses propriétés algébriques, le nombre plastique a des applications en combinatoire et en géométrie.
Autosimilarité en dimension trois
Une propriété géométrique intrigante du nombre plastique est sa relation avec des structures autosimilaires en trois dimensions. Par exemple, si l’on considère un parallélépipède dont les dimensions respectent les rapports \(\rho\), on peut retirer un sous-parallélépipède tout en conservant les proportions originales.
Cela est analogue à la propriété bien connue du rectangle d’or, mais étendue à une dimension supplémentaire, soulignant la nature unique de \(\rho\).
Liens avec les polynômes de Tchebychev
Le nombre plastique est également lié aux polynômes de Tchebychev de premier et deuxième types, qui apparaissent dans la résolution d’équations différentielles et dans la théorie des nombres. En particulier, \(\rho\) est associé à la racine principale d’un polynôme de Thebychev modifié, ce qui ouvre des perspectives pour son utilisation dans des contextes combinatoires et analytiques.
Aller plus loin sur le nombre plastique
Le nombre plastique est à l’origine de nombreuses recherches et nombreux problèmes mathématiques. Pour y voir plus clair, voici une cartographie de l’ensemble des recherches tournant autour (et de la suite de Fibonacci) :
| Tableau de correspondances suites/nombres (en lien avec Fibonacci/nombres métalliques) |
|
| Suites | Nombres |
| Suite de Fibonacci | Nombre d’or |
| Suite de Pell | Nombre d’argent |
| Généralisation de Fibonacci : les suites k-bonacci | Nombres métalliques : généralisation du nombre d’or |
| Suite de Lucas | Nombre de Lucas |
| Suite de Padovan | Nombre plastique |
| Suite de Perrin | Nombres pseudo-premiers de Perrin |
| Suite de Jacobsthal | Nombres oblongs de Jacobsthal |
| Polynôme/suite de Narayana | Nombre de Narayana |
| Nombre de Gildas | |
| Nombre de Keith | |
| Super nombre d’or | |
Conclusion
Le nombre plastique \(\rho\) est un nombre irrationnel fascinant qui émerge naturellement de l’étude des équations cubiques. Sa structure complexe et ses propriétés algébriques et géométriques en font un objet d’étude riche et stimulant. Bien que moins connu que d’autres constantes mathématiques, \(\rho\) offre un terrain fertile pour explorer des concepts avancés en mathématiques, que ce soit dans le cadre de la théorie des suites récurrentes, de la géométrie ou de l’analyse. Son unicité en tant que solution positive d’une équation cubique simple en fait une constante digne d’une attention particulière dans les études mathématiques.
Ainsi, bien que ce nombre soit hors programme, la compréhension approfondie des propriétés liées à cette notion te permettra d’améliorer tes compétences en analyse et en algèbre. Pour t’entraîner sur cette notion, tu peux réaliser les sujets suivants :
- Ecricome 2018 (mathématiques approfondies),
- Maths 1 HEC 2009 (mathématiques appliquées),
- la première Question Sans Préparation des Oraux HEC 2023.
Tu peux retrouver le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder à toutes nos autres ressources mathématiques.