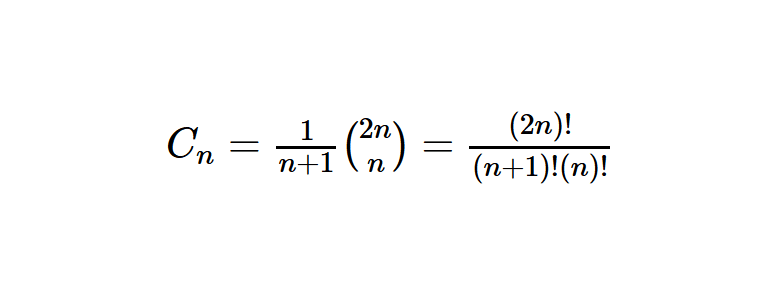Les notions hors programme sont particulièrement importantes pour quiconque prétendant à une Parisienne. À ce titre, être familier avec les nombres de Catalan permettra de se préparer face à de telles épreuves. Toutefois, les nombres de Catalan sont également présents sur des sujets EDHEC/Emlyon. Initialement liés au dénombrement, les nombres de Catalan te permettront de t’exercer également sur les sommes/produits ou sur les probabilités discrètes, étant donné leurs nombreuses applications en mathématiques.
Définition des nombres de Catalan
Définition mathématique
On définit les nombres de Catalan de la manière suivante :
\[ \forall n \in \mathbb{N}\ , C_n = \frac{1}{n+1} {{2n}\choose{n}} = \frac{(2n)!}{(n+1)!(n)!} = {{2n}\choose{n}} – {{2n}\choose{n+1}}\]
Par exemple, il est clair d’après la première définition que :
\(C_0 = \frac{1}{1+0}{{0}\choose{0}} = 1 \)
En procédant de la même manière, on peut retrouver les premières valeurs de \( C_n\) :
\( C_1 = 1\)
\( C_2 = 2\)
\( C_3 = 5\)
\( C_4 = 14\)
Interprétation en dénombrement
Notons avant tout que la troisième définition mathématique des nombres de Catalan que nous avons avancée (celle en tant que différence de deux coefficients binomiaux) permet de montrer directement que \( C_n\) est bien un entier en tant que différence de deux entiers. Cela nous permet de donner un sens plus précis dans le cadre de l’interprétation géométrique des nombres de Catalan.
Passons par un peu d’histoire mathématique pour appréhender cette notion : si ces nombres ont pris le nom du mathématicien Eugène Charles Catalan, qui a approfondi leur étude, c’est en 1751 que Leonhard Euler a cherché à répondre à la question suivante : De combien de façon peut-on découper un polygone de \(n\)-cotés en \(n-2\) triangles ? Spoil : Ce nombre de possibilités apparaît être précisément l’entier \(C_n\) !
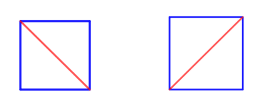
Pour mieux comprendre cette interprétation géométrique, travaillons dans des cas particuliers plus simples. Dans le cas du carré, on voit ici les deux moyens de couper la forme en \(4-2 = 2\) triangles. On retrouve la valeur de \(C_2\) !
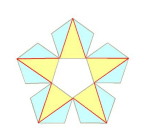
Plus complexe, alors que l’on reste dans des petits cas particuliers : voici les cinq manières de trianguler un pentagone. On obtient donc un total de cinq possibilités : on a bien la valeur de \(C_3\) !
En itérant ce même procédé, Euler trouve toutes les combinaisons jusqu’au décagone et conjecture la formule suivante, dont le lien avant le nombre \( E_n\) peut être réalisé en repartant de la définition de \( E_n\) montrée plus haut et en écrivant le coefficient binomial en extension. \(E_{n-2} = \frac{2\times4\times…(4n-10)}{2\times 3\times 4\times …(n-1)} \)
Propriétés des nombres de Catalan
Trois autres écritures du nombre de Catalan
Sous forme de produit
Le nombre de Catalan d’ordre n peut également s’écrire sous la forme d’un produit : \( \forall n\ge 2, C_n = \displaystyle \prod_{k=2}^{n} \frac{n+k}{k} \)
Voici la démonstration rapide de cette formule qui permet de s’exercer un peu avec les produits :
\(\forall n\ge 2, C_n = \displaystyle \prod_{k=2}^{n} \frac{n+k}{k} = \frac{\displaystyle \prod_{k=2}^{n} (n+k)}{\displaystyle \prod_{k=2}^{n} (k)} = \frac{(n+2)…(2n-1)(2n)}{n!} = \frac{n+1}{n+1} \times \frac{(n+2)…(2n-1)(2n)}{n!} =\frac {(n+1)…(2n)}{(n+1)!}\).
Or, comme on a précisément que \( \frac{(2n)!}{n!} = (n+1)…(2n) \), on conclut que \( C_n = \frac{(2n)!}{(n!)(n+1)!} \)
Formule de récurrence
De plus, le nombre de Catalan d’ordre n possède une autre écriture sous forme de récurrence :
On a : \( \forall n \in
\mathbb{N}, C_{n+1}= \frac{2(2n+1)}{n+1}C_n\)
À partir de cette écriture, il est possible de retrouver l’écriture du terme général du nombre de Catalan à l’ordre n. La démonstration est assez triviale, je te laisse la faire pour t’exercer à la manipulation des coefficients binomiaux (indice : récurrence, comme souvent avec les suites).
Formule de récurrence forte
Voici enfin une autre formule de récurrence qui permet d’exprimer le nombre de Catalan d’ordre n en fonction de tous les précédents. Pour la démonstration de cette formule, il convient d’opérer par récurrence.
On a : \(\forall n\ge 1, C_n =\left(\displaystyle \sum_{k=1}^{n-1} C_k\times C_{n-k-1} \right)\)
Équivalent et limite du nombre de Catalan
On a le résultat suivant que l’on peut redémontrer en repartant de l’équivalent de Stirling :
\[C_n \underset{+\infty}{\sim} \frac{4^n}{n^{3/2} \sqrt(n)} \]
Démonstration
Pour rappel, voici l’équivalent de Stirling qui, même s’il n’est pas explicitement au programme, est parfois nécessaire lors de certains oraux de Parisiennes, mais qui sera systématiquement rappelé si nécessaire lors des sujets d’écrit : \(n! \underset{+\infty}{\sim} n^{n+\frac{1}{2}} e^{-n}\sqrt{2\pi} \).
Or, \(C_n = \frac{(2n)!}{(n+1)!(n)!} \) donc par compatibilité de l’équivalence avec le produit et le quotient, on a : \(C_n \underset{+\infty}{\sim} \frac{{2n}^{{2n}+\frac{1}{2}} e^{-2n}\sqrt{2\pi} }{{(n+1)}^{{(n+1}+\frac{1}{2})} e^{-n-1}\sqrt{2\pi} {n^{(n+\frac{1}{2})} e^{-n}\sqrt{2\pi}}} = \frac{4^n}{n^{3/2} \sqrt(n)} \) (obtenu en simplifiant au maximum la fraction !).
Déduisons alors de cet équivalent la limite de \(C_n\) : on a \( \frac{4^n}{n^{3/2} \sqrt(n)} = \frac{(2^n)\times (2^n)}{n^{3/2} \sqrt(n) }= \frac{2^n}{n^{3/2}}\times \frac{2^n}{\sqrt{n}} \). D’une part, la première fraction tend vers \(+\infty\) par un argument de croissances comparées et on conclut de même pour la deuxième fraction. Par produit, il est alors clair que \(\lim \limits_{n \to +\infty} C_n= +\infty\)
Application en dénombrement (problème des mots de Dyck)
Un mot de Dyck est une succession de caractères X et Y de telle sorte que le mot entier soit composé de n lettres. Par exemple, dans le cas n = 6, XXXYYX est un mot de Dyck tout comme XYXYYX. Cherchons alors le nombre de mots de Dyck tel que, lorsque nous parcourons le mot de gauche à droite, il y ait toujours plus de X que de Y.
Par exemple, XXYYXX convient puisque, à n’importe quelle lettre où l’on regarde, il y a toujours plus de X que de Y derrière. À l’inverse, XYYXXX ne convient pas puisque, de la première à la troisième lettre, il y a un seul X et deux Y. Maintenant que le problème est posé, il est possible de montrer que pour un mot de Dyck à n-lettres, il y a \(C_n\) mots de Dyck solutions du problème.
La partie C du deuxième problème de la maths Emlyon 2022 en mathématiques approfondies est d’ailleurs consacrée à cette démonstration !
Calcul du nombre de Catalan d’ordre n en Python
Voici deux méthodes pour calculer en Python la valeur de \(C_n\) en repartant de deux expressions mathématiques différentes.
Pour la première formule : \(C_{n+1}= \frac{2(2n+1)}{n+1}C_n\) avec \( C_o = 1\)
Notons ici l’importance du décalage d’indice lorsque l’on est dans la boucle afin de bien calculer le terme d’après en fonction du terme de Catalan précédent.
Pour la deuxième formule, prenons : \( C_n = \frac{1}{n+1} {{2n}\choose{n}} \) (cela permettra de réviser la manière d’utiliser la fonction factorielle !)
Conclusion
Les nombres de Catalan sont donc au fondement du dénombrement et font également appel à un très grand nombre de notions annexes telles que la manipulation des coefficients binomiaux, des sommes et produits, mais sont également très facilement applicables à du Python. Ils permettent donc de vérifier sa maîtrise d’un grand nombre de notions au cœur du programme de mathématiques appliquées et approfondies.
Si tu souhaites t’entraîner sur la notion, le sujet de mathématiques approfondies de l’Emlyon de 2022 consacre un de ses deux exercices sur la question, en passant par de multiples approches pour mieux comprendre ce fameux nombre de Catalan, des suites aux probabilités.
À lire aussi : Suite de Fibonacci (hors programme ECG)
Tu peux retrouver ici le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder ici à toutes nos autres ressources mathématiques !