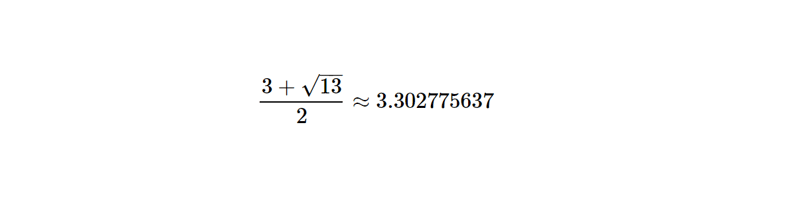Le nombre d’or, souvent noté \(\varphi\), est l’un des nombres irrationnels les plus célèbres en mathématiques. Il est réputé pour ses propriétés esthétiques et ses apparitions dans l’art, l’architecture et la nature. Mais \(\varphi\) n’est pas le seul nombre irrationnel d’intérêt. Les mathématiciens ont identifié d’autres « nombres métalliques » qui partagent des propriétés similaires, mais présentent des valeurs et des caractéristiques distinctes. Dans cet article, nous explorerons ces dérivés du nombre d’or, en nous concentrant sur les nombres d’argent, de bronze, et nous aborderons également les cas particuliers du cuivre, du nickel, du cobalt, du fer et du plastique.
Rappel : les nombres métalliques
Les nombres métalliques forment une famille de nombres irrationnels qui généralisent la définition du nombre d’or. Chacun d’eux est défini par une équation de la forme :
\[
M_n = \frac{n + \sqrt{n^2 + 4}}{2}
\]
où \(n\) est un entier positif.
Le nombre d’or correspond au cas où \(n = 1\), mais d’autres valeurs de \(n\) donnent naissance à d’autres nombres métalliques, chacun avec ses propres applications et propriétés.
Le nombre d’argent
Le nombre d’argent est le premier dérivé notable du nombre d’or, correspondant à \(n = 2\) dans l’équation générale. Il est défini par :
\[
\delta_S = \frac{2 + \sqrt{4 + 4}}{2} = 1 + \sqrt{2} \approx 2,414
\]
Le nombre d’argent apparaît dans de nombreuses configurations géométriques, notamment dans les rectangles d’argent, analogues aux rectangles d’or, mais basés sur ce rapport particulier. Comme \(\varphi\), \(\delta_S\) est également lié à une suite récurrente, similaire à celle de Fibonacci, mais avec des coefficients différents, définie par :
\[
S_n = 2S_{n-1} + S_{n-2}
\]
où les termes initiaux sont généralement \(S_0 = 0\) et \(S_1 = 1\). Cette suite croît également de manière exponentielle avec un taux déterminé par \(\delta_S\).
Le nombre de bronze
Le nombre de bronze, noté \(\delta_B\), est un autre membre important de la famille des nombres métalliques. Il est obtenu en prenant \(n = 3\) dans la formule générale des nombres métalliques :
\[
\delta_B = \frac{3 + \sqrt{9 + 4}}{2} = \frac{3 + \sqrt{13}}{2} \approx 3,302775637
\]
Comme pour les autres nombres métalliques, le nombre de bronze est la solution d’une équation quadratique spécifique :
\[
\delta_B^2 – 3\delta_B – 1 = 0
\]
Ce nombre est associé à une suite récurrente semblable à celle de Fibonacci, mais adaptée à sa valeur. Cette suite, souvent appelée suite de Padovan généralisée pour \(n = 3\), est définie par la relation suivante :
\[
B_n = 3B_{n-1} + B_{n-2}
\]
avec des conditions initiales, par exemple, \(B_0 = 0\) et \(B_1 = 1\).
La croissance de cette suite est asymptotiquement exponentielle, avec un taux de croissance donné par \(\delta_B\). Cette suite récurrente est aussi reliée à la géométrie, notamment dans la construction de spirales de bronze, qui sont analogues aux spirales d’or, mais basées sur le rapport du nombre de bronze.
De plus, le nombre de bronze intervient dans des contextes algébriques et combinatoires. Par exemple, il apparaît dans les problèmes liés aux carrelages, où les pavages de rectangles avec des dominos peuvent être analysés via des suites récurrentes associées au nombre de bronze. Ainsi, bien que moins connu que le nombre d’or ou d’argent, \(\delta_B\) possède ses propres applications et constitue un sujet d’étude intéressant en mathématiques.
Les constantes de p-nacci : d’autres nombres métalliques
En poursuivant l’exploration des nombres métalliques, une généralisation naturelle consiste à étendre le concept aux récurrences de degré supérieur, donnant naissance aux constantes de p-nacci. Ces constantes, notées \(\alpha_p\), sont les solutions positives de l’équation caractéristique associée à une récurrence linéaire de type p-nacci, définie par :
\[
x^p = 1 + x + x^2 + \ldots + x^{p-1}
\]
où \(p\) représente le degré de la récurrence.
Pour des petites valeurs de \(p\), certaines de ces constantes peuvent être exprimées à l’aide de radicaux, mais cette possibilité disparaît pour des valeurs plus élevées de \(p\), où les expressions deviennent trop complexes pour être représentées simplement.
Les premières constantes de p-nacci
Le nombre de cuivre
Le nombre de cuivre, correspondant à \(p = 4\), possède une expression par radicaux qui fait intervenir des racines cubiques complexes. Il est défini par l’expression :
\[
\alpha_4 = \sqrt[3]{65 + 3\sqrt{1689}}
\]
Sa valeur numérique approximative est \(\alpha_4 \approx 1,927561975.\)
Le nombre de nickel
Le nombre de nickel, correspondant à \(p = 5\), ne peut pas être exprimé simplement par des radicaux. Il possède une valeur numérique approximative de \(\alpha_5 \approx 1,9659482366,\) et est associé à la suite récurrente de Pentanacci.
Le nombre de cobalt
Le nombre de cobalt, correspondant à \(p = 6\), ne dispose pas non plus d’une expression par radicaux. Sa valeur numérique est approximativement \(\alpha_6 \approx 1,983582843,\) et il est relié à la suite récurrente de Hexanacci.
Le nombre de fer
Le nombre de fer, correspondant à \(p = 7\), n’a pas d’expression par radicaux, tout comme les autres nombres métalliques de degré élevé. Sa valeur numérique est \(\alpha_7 \approx 1,991964197,\) et il est associé à la suite récurrente de Heptanacci.
Le super nombre d’or
Le super nombre d’or, également appelé « radian d’or », est une extension du nombre d’or classique. Il est défini comme la solution positive de l’équation :
\[
x^3 = x^2 + 1
\]
Sa valeur approximative est \(\varphi_3 \approx 1,465571231.\) Ce nombre apparaît dans des contextes liés aux ratios et aux proportions qui nécessitent une généralisation du nombre d’or au-delà des relations quadratiques. Le super nombre d’or est particulièrement pertinent dans la conception d’espaces et d’objets qui cherchent à harmoniser des proportions complexes, tout en conservant une structure géométrique élégante et équilibrée.
Le nombre plastique
Le nombre plastique est une constante mathématique unique qui diffère des autres nombres métalliques par sa définition cubique. Il est la solution positive de l’équation :
\[
x^3 = x + 1
\]
Sa valeur numérique approximative est \(\alpha_3 \approx 1,3247.\) Le nombre plastique apparaît dans divers domaines tels que l’architecture, le design et la modélisation de la croissance naturelle, en raison de ses propriétés esthétiques et proportionnelles harmonieuses. Il peut également être observé dans certaines structures fractales et géométriques complexes.
Aller plus loin sur la suite de Fibonacci
La suite de Fibonacci est à l’origine de nombreuses recherches et nombreux problèmes mathématiques. Pour y voir plus clair, voici une cartographie de l’ensemble des recherches tournant autour de la suite de Fibonacci (et du nombre d’or) :
| Tableau de correspondances suites/nombres (en lien avec Fibonacci/nombres métalliques) |
|
| Suites | Nombres |
| Suite de Fibonacci | Nombre d’or |
| Suite de Pell | Nombre d’argent |
| Généralisation de Fibonacci : les suites k-bonacci | Nombres métalliques : généralisation du nombre d’or |
| Suite de Lucas | Nombre de Lucas |
| Suite de Padovan | Nombre plastique |
| Suite de Perrin | Nombres pseudo-premiers de Perrin |
| Suite de Jacobsthal | Nombres oblongs de Jacobsthal |
| Polynôme/suite de Narayana | Nombre de Narayana |
| Nombre de Gildas | |
| Nombre de Keith | |
| Super nombre d’or | |
Conclusion
Les nombres métalliques, dont le nombre d’or est le représentant le plus célèbre, forment une famille riche de nombres irrationnels avec des propriétés fascinantes. En explorant les dérivés du nombre d’or, comme les nombres d’argent, de bronze, de cuivre, de nickel, de cobalt, de fer et de plastique, nous découvrons des suites récurrentes associées et des taux de croissance exponentiels qui montrent la profondeur et la diversité de ces concepts mathématiques. Chacun de ces nombres a ses propres applications et ses propres domaines d’intérêt, offrant une variété d’outils pour les mathématiciens et les amateurs de curiosités numériques.
Ainsi, bien que cette notion soit hors programme, la compréhension approfondie de cette dernière te permettra d’améliorer des compétences en analyse et en algèbre, te préparant donc pour les épreuves écrites et orales de mathématiques. Pour t’entraîner sur cette notion, tu peux réaliser les sujets suivants : Ecricome 2018 (mathématiques approfondies) et la première Question Sans Préparation des Oraux HEC 2023.
Tu peux retrouver le méga-répertoire qui contient toutes les annales de concours et les corrigés ! Tu peux également accéder à toutes nos autres ressources mathématiques !