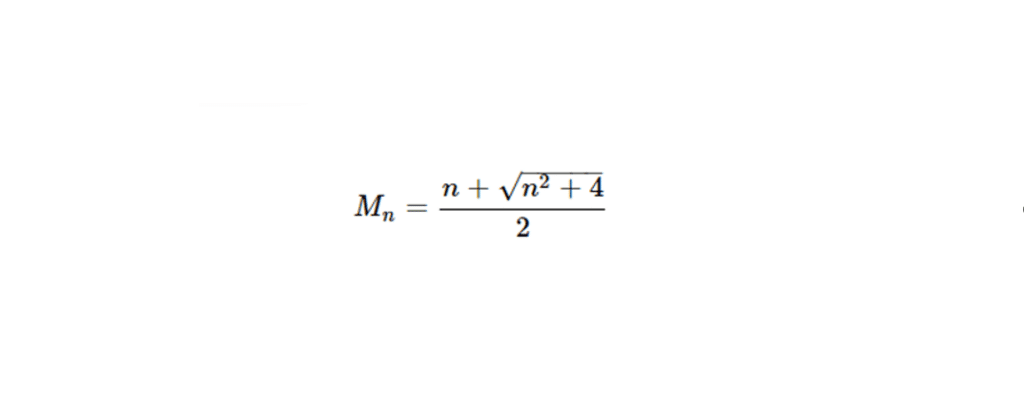Les nombres métalliques sont une famille de nombres irrationnels qui généralisent le célèbre nombre d’or \(\varphi\). Ils se caractérisent par des propriétés mathématiques intéressantes et des apparitions dans divers domaines tels que la géométrie, la nature et les systèmes dynamiques. Chaque nombre métallique est associé à un métal, d’où leur nom, comme le nombre d’or (\(\varphi\)) associé à l’or, le nombre d’argent (\(\sigma\)), le nombre de cuivre, etc. Ces nombres sont définis par une relation récurrente qui ressemble à celle du nombre d’or, mais généralisée pour chaque métal. Ces nombres restent liés d’une manière ou d’une autre à la fameuse suite de Fibonacci.
Définition des nombres métalliques
Les nombres métalliques sont définis par une relation récurrente du type :
\[
M_n = \frac{n + \sqrt{n^2 + 4}}{2}
\]
où \(n\) est un entier positif. Le nombre métallique correspondant est souvent noté \(M_n\), où \(n\) indique le métal associé.
De plus, les nombres métalliques sont la solution d’une équation quadratique particulière :
\[
x^2 – nx – 1 = 0
\]
Quelques exemples notables de nombres métalliques :
- \(M_1\) : Le nombre d’or \(\phi = \frac{1 + \sqrt{5}}{2} \approx 1,618\)
- \(M_2\) : Le nombre d’argent \(\sigma = \frac{2 + \sqrt{8}}{2} \approx 2,414\)
- \(M_3\) : Le nombre de bronze \(\approx 3,302\)
Démonstration de la forme générale des nombres métalliques
Pour démontrer la forme générale des nombres métalliques \(M_n\), considérons l’équation quadratique dont ils sont la solution :
\[
x^2 – nx – 1 = 0
\]
Cette équation caractérise le nombre métallique \(M_n\). Pour trouver les solutions, nous appliquons la formule quadratique générale :
\[
x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}
\]
où \(a = 1\), \(b = -n\), et \(c = -1\). En substituant ces valeurs, nous obtenons :
\[
x = \frac{-(-n) \pm \sqrt{(-n)^2 – 4 \cdot 1 \cdot (-1)}}{2 \cdot 1}
\]
\[
x = \frac{n \pm \sqrt{n^2 + 4}}{2}
\]
Les solutions de cette équation sont donc :
\[
x_1 = \frac{n + \sqrt{n^2 + 4}}{2} \quad \text{et} \quad x_2 = \frac{n – \sqrt{n^2 + 4}}{2}
\]
Le nombre métallique \(M_n\) est défini comme la solution positive, donc nous retenons \(x_1\) :
\[
M_n = \frac{n + \sqrt{n^2 + 4}}{2}
\]
Ainsi, nous retrouvons la forme générale des nombres métalliques. Cette démonstration non seulement justifie leur définition, mais montre aussi comment la structure de l’équation quadratique influence directement la nature et les propriétés des nombres métalliques.
Diverses expressions
Les nombres métalliques peuvent être définis comme la solution positive de l’équation quadratique du second degré \(x^2 = nx + 1\), ce qui donne l’expression suivante pour le nombre métallique d’indice \(p\) :
\[
\varphi_n = \frac{n + \sqrt{n^2 + 4}}{2}
\]
En réarrangeant cette équation sous la forme \(x = n + \frac{1}{x}\), on obtient un développement en fraction continue :
\[
\varphi_n = n + \frac{1}{n + \frac{1}{n + \frac{1}{n + \cdots}}}
\]
En exprimant l’équation sous la forme \(x = \sqrt{1 + nx}\), on peut la réécrire sous forme de radical imbriqué infini :
\[
\varphi_n = \sqrt{1 + n\sqrt{1 + n\sqrt{1 + n\sqrt{1 + \cdots}}}}
\]
De plus, le \(n\)-ième nombre métallique peut également être exprimé sous forme d’intégrale :
\[
\varphi_n = \int_0^n \left(\frac{x}{2\sqrt{x^2 + 4}} + \frac{n + 2}{2n}\right)dx
\]
Propriétés des nombres métalliques
Les nombres métalliques possèdent plusieurs propriétés remarquables qui les rendent intéressants tant d’un point de vue théorique que pratique.
Relation récurrente
Chaque nombre métallique \(M_n\) satisfait une équation quadratique de la forme :
\[
M_n^2 = n \cdot M_n + 1
\]
Cette relation est analogue à celle du nombre d’or, qui satisfait \(\varphi^2 = \varphi + 1\). Cette propriété peut être démontrée en utilisant la définition de \(M_n\) et en manipulant l’expression pour montrer que l’équation est bien vérifiée.
Forme récurrente de la suite associée
Les nombres métalliques peuvent être associés à une suite récurrente, similaire à la suite de Fibonacci pour le nombre d’or. Pour chaque \(n\), il existe une suite \(S_n\) définie par :
\[
S_{k+1} = n \cdot S_k + S_{k-1}
\]
avec des conditions initiales spécifiques (souvent \(S_0 = 0\) et \(S_1 = 1\)). Le rapport des termes successifs de cette suite converge vers le nombre métallique \(M_n\).
Approximation continue
Les nombres métalliques sont souvent irrationnels et peuvent être approximés par des fractions continues. La fraction continue associée à \(M_n\) est périodique, reflétant ainsi leur structure interne répétitive. Par exemple, le nombre d’or \(\phi\) a la fraction continue simple suivante :
\[
\phi = [1; 1, 1, 1, \dots]
\]
Pour \(M_2\) (le nombre d’argent), la fraction continue est :
\[
\sigma = [2; 2, 2, 2, \dots]
\]
Cette périodicité est une caractéristique des nombres métalliques.
Applications en géométrie
Les nombres métalliques apparaissent naturellement dans certains problèmes géométriques, notamment dans l’étude des polygones réguliers et des spirales. Par exemple, le nombre d’or est étroitement lié au pentagone régulier et à la spirale d’or, tandis que le nombre d’argent apparaît dans le contexte de l’hexagone et d’autres structures symétriques.
Les nombres métalliques et les matrices
Les nombres métalliques peuvent également être étudiés à travers le prisme des matrices, offrant ainsi une perspective linéaire et algébrique sur ces nombres. Considérons une matrice \(2 \times 2\) spécifique associée à chaque nombre métallique \(M_n\) :
\[
A_n = \begin{pmatrix}
n & 1 \\
1 & 0
\end{pmatrix}
\]
Le nombre métallique \(M_n\) est alors l’une des valeurs propres de cette matrice \(A_n\). En effet, les valeurs propres \(\lambda\) de \(A_n\) sont les solutions de l’équation caractéristique \(\lambda^2 – n\lambda – 1 = 0\), qui est exactement l’équation quadratique dont \(M_n\) est la solution positive. Cette approche matricielle permet non seulement de comprendre les nombres métalliques dans le contexte des systèmes dynamiques, mais aussi de les utiliser pour analyser des transformations linéaires et des suites récurrentes.
Par exemple, en étudiant les puissances successives de la matrice \(A_n\), on peut générer les termes de la suite récurrente associée au nombre métallique \(M_n\), offrant ainsi une méthode efficace pour explorer les propriétés des suites et des séries liées à ces nombres. Cette connexion entre nombres métalliques et matrices met en lumière leur rôle central dans divers domaines des mathématiques, en particulier dans l’algèbre linéaire.
À lire également : Matrices de Fibonacci.
Le rectangle métallique
Un rectangle métallique est un rectangle dont les proportions sont données par un nombre métallique \(M_n\). Plus précisément, un rectangle métallique a une longueur \(L\) et une largeur \(l\) telles que le rapport \( \displaystyle \frac{L}{l} = M_n \). Ces rectangles généralisent l’idée du célèbre rectangle d’or, associé au nombre d’or \(\varphi,\) en introduisant d’autres proportions basées sur les différents nombres métalliques.
Une propriété remarquable des rectangles métalliques est que, lorsqu’on leur retire un carré de côté égal à leur largeur, le rectangle restant conserve les mêmes proportions que le rectangle original, ce qui en fait un objet géométrique d’une grande élégance mathématique.
Aller plus loin sur les nombres métalliques
Les nombres métalliques sont à l’origine de nombreuses recherches et nombreux problèmes mathématiques. Pour y voir plus clair, voici une cartographie de l’ensemble des recherches tournant autour (et de la suite de Fibonacci) :
| Tableau de correspondances suites/nombres (en lien avec Fibonacci/nombres métalliques) |
|
| Suites | Nombres |
| Suite de Fibonacci | Nombre d’or |
| Suite de Pell | Nombre d’argent |
| Généralisation de Fibonacci : les suites k-bonacci | Nombres métalliques : généralisation du nombre d’or |
| Suite de Lucas | Nombre de Lucas |
| Suite de Padovan | Nombre plastique |
| Suite de Perrin | Nombres pseudo-premiers de Perrin |
| Suite de Jacobsthal | Nombres oblongs de Jacobsthal |
| Polynôme/suite de Narayana | Nombre de Narayana |
| Nombre de Gildas | |
| Nombre de Keith | |
| Super nombre d’or | |
Conclusion
Les nombres métalliques constituent une généralisation fascinante du nombre d’or, offrant une multitude de propriétés mathématiques intéressantes et des applications dans divers domaines. Leur étude permet de mieux comprendre la structure des suites récurrentes, les fractions continues et leurs liens avec la géométrie. En élargissant notre compréhension des nombres métalliques, nous découvrons des connexions profondes entre les mathématiques, la nature et les structures algébriques, renforçant ainsi l’importance de ces nombres dans l’étude des systèmes dynamiques et des formes géométriques.
Ainsi, bien que ces nombres soient hors programme, la compréhension approfondie des propriétés liées à cette notion te permettra d’améliorer tes compétences en analyse et en algèbre. Pour t’entraîner sur cette notion, tu peux réaliser les sujets suivants :
- Ecricome 2018 (mathématiques approfondies),
- Maths 1 HEC 2009 (mathématiques appliquées),
- la première Question Sans Préparation des Oraux HEC 2023.
Tu peux retrouver le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder à toutes nos autres ressources mathématiques.