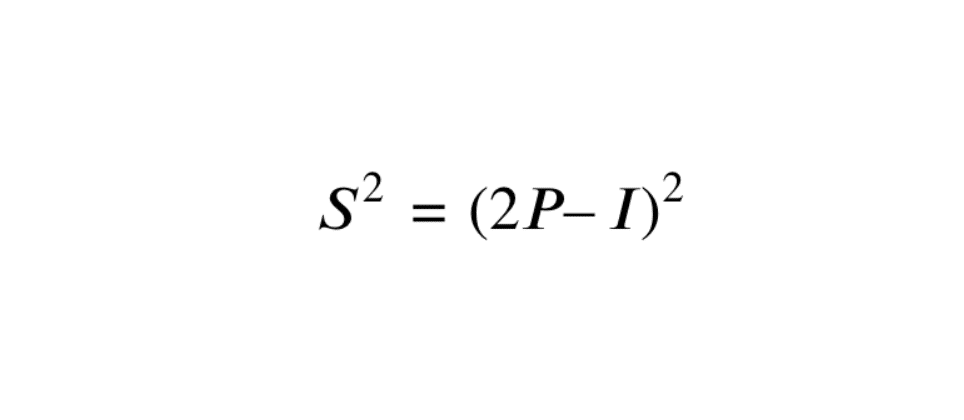Dans le vaste domaine des mathématiques, les notions de projecteurs et de symétries occupent une place particulière, surtout dans l’étude des espaces vectoriels et des transformations linéaires. Cet article se propose d’explorer en profondeur ces concepts, en présentant des propriétés avancées souvent omises dans le programme mais qui sont d’une grande utilité pour comprendre la structure interne des espaces vectoriels. En dépit de leur abstraction, ces notions sont des outils puissants pour analyser et résoudre des problèmes mathématiques complexes.
Présentation des projecteurs et des symétries
Les projecteurs
Un projecteur (ou projection) dans un espace vectoriel est un endomorphisme \( P \) tel que \( P^2 = P \). Cette propriété caractérise les applications linéaires qui “répètent” leur effet après la première application. Géométriquement, un projecteur sur un espace vectoriel projette des vecteurs sur un sous-espace, de manière à ce que la projection d’un vecteur déjà dans ce sous-espace soit le vecteur lui-même.
Les symétries
Une symétrie, dans le contexte des espaces vectoriels, est un endomorphisme \( S \) pour lequel \( S^2 = I \), où \( I \) est l’application identité. Cela signifie que l’application d’une symétrie deux fois de suite ramène tout vecteur à sa position initiale. Les symétries sont souvent utilisées pour décrire des réflexions ou des inversions à travers un sous-espace.
Propriétés avancées des projecteurs
La trace d’un projecteur vaut son rang
La trace d’un projecteur est un concept mathématique important, en particulier car elle est égale au rang du projecteur. Cela fournit une liaison élégante entre deux propriétés significatives de l’endomorphisme : sa trace, qui est la somme des valeurs propres comptées avec leur multiplicité algébrique, et son rang, le nombre de dimensions de son image.
Considérons un projecteur \( P \) dans un espace vectoriel \( V \) de dimension finie. Rappelons qu’un projecteur \( P \) est caractérisé par la propriété \( P^2 = P \). Les valeurs propres d’un projecteur sont \( 0 \) et \( 1 \), car si \( v \) est un vecteur propre associé à la valeur propre \( \lambda \), nous avons \( P^2v = Pv = \lambda v \) et \( P^2v = P(\lambda v) = \lambda Pv = \lambda^2 v \), ce qui implique que \( \lambda^2 = \lambda \). Ainsi, \( \lambda \) doit être \( 0 \) ou \( 1 \).
Dans cette configuration, la trace de \( P \), notée \( \text{Tr}(P) \), est égale à la somme des valeurs propres de \( P \). Comme les valeurs propres de \( P \) sont \( 0 \) et \( 1 \), et que chaque vecteur propre associé à la valeur propre \( 1 \) contribue à \( 1 \) dans la trace, la trace de \( P \) correspond au nombre de fois que la valeur propre \( 1 \) apparaît, c’est-à-dire au nombre de vecteurs propres linéairement indépendants associés à cette valeur propre, qui est également la dimension de l’image de \( P \).
Formellement, si \( \dim(\text{Im}(P)) = r \), alors il y a \( r \) valeurs propres \( 1 \) dans la décomposition spectrale de \( P \), toutes les autres étant \( 0 \). Ainsi, \( \text{Tr}(P) = r \) et par définition du rang d’un endomorphisme, qui est la dimension de son image, nous avons \( \text{Rg}(P) = r \).
Ceci démontre que la trace d’un projecteur est égale à son rang. Cette propriété offre une méthode rapide et élégante pour calculer le rang d’un projecteur en examinant uniquement sa trace, ce qui peut simplifier l’analyse des projecteurs dans des contextes plus complexes.
La représentation avec des matrices par bloc
Chaque projecteur dans un espace vectoriel de dimension finie et diagonalisable (avec les valeurs propres 1 et 0, excluant l’identité et la matrice nulle) peut être exprimé de manière particulièrement simplifiée. Supposons que \( B = (e_1, \ldots, e_r, e_{r+1}, \ldots, e_n) \) constitue une base de l’espace vectoriel \( E \), où \( e_1, \ldots, e_r \) appartiennent à l’image de \( p \) (Im(\( p \))) et \( e_{r+1}, \ldots, e_n \) appartiennent au noyau de \( p \) (Ker(\( p \))). Cette configuration est possible parce que l’image et le noyau de \( p \) sont des sous-espaces supplémentaires.
Dans cette base spécifiquement arrangée, la matrice représentant \( p \) se présente comme suit :
\[
\text{Mat}_B(p) = \begin{pmatrix} I_r & 0 \\ 0 & 0_{n-r} \end{pmatrix}
\]
où \( I_r \) est la matrice identité de taille \( r \) et \( 0_{n-r} \) est une matrice nulle de taille \( n-r \). De cette représentation découlent les propriétés suivantes :
– Les éléments diagonaux sont exclusivement des 1 et des 0, reflétant directement les valeurs propres de \( p \).
– Tous les autres éléments de la matrice sont nuls.
Le nombre de 1 présents sur la diagonale est équivalent au rang du projecteur.
Propriétés avancées des symétries
Les valeurs propres d’une symétrie
D’un point de vue spectral, les valeurs propres d’une symétrie \( S \) sont toujours \( \pm 1 \). Cela signifie que toute transformation linéaire qui est une symétrie va refléter ou inverser les éléments de l’espace vectoriel à travers un ou plusieurs sous-espaces. Mathématiquement, cela implique que l’espace vectoriel \( V \) peut être décomposé en une somme directe \( V = V_1 \oplus V_{-1} \), où \( V_1 \) et \( V_{-1} \) sont les sous-espaces propres associés respectivement aux valeurs propres \( 1 \) et \( -1 \) de \( S \). Cette décomposition est directement liée à la structure de \( S \) et révèle comment \( S \) agit différemment sur différents composants de l’espace.
Réflexion et renversement
Dans un espace vectoriel \( E \), considérons deux sous-espaces \( F \) et \( G \) qui sont supplémentaires, c’est-à-dire que chaque vecteur \( x \) dans \( E \) peut être écrit de manière unique comme la somme \( x = y + z \) où \( y \) appartient à \( F \) et \( z \) à \( G \). Cette décomposition permet de définir des transformations spécifiques, en particulier la notion de symétrie par rapport à \( F \) parallèlement à \( G \).
La symétrie par rapport à \( F \) parallèlement à \( G \) est une application linéaire \( s \) qui, à tout vecteur \( x \) dans \( E \), associe le vecteur \( s(x) = y – z \), où \( y \) est la composante de \( x \) dans \( F \) et \( z \) la composante de \( x \) dans \( G \). Cette transformation garde inchangée la composante dans \( F \) tout en inversant la composante dans \( G \), reflétant ainsi \( x \) par rapport à \( F \) tout en conservant sa “projection” sur \( F \) inchangée.
Cette définition de symétrie s’élargit pour inclure les notions spécifiques de réflexion et de renversement, qui sont deux cas particuliers de symétries orthogonales.
La réflexion est définie dans le cas où le sous-espace \( F \) est de dimension \( n-1 \), ce qui implique que \( s \) agit comme une inversion à travers un hyperplan.
D’autre part, un renversement se produit lorsque la dimension de \( F \) est \( n-2 \), où \( s \) inverse l’orientation le long d’un axe, en laissant le reste de l’espace majoritairement inchangé. Ces transformations sont fondamentales pour comprendre la structure géométrique et les symétries dans les espaces vectoriels.
Relations entre projecteurs et symétries
Les projecteurs et les symétries peuvent être étroitement liés par des expressions algébriques, illustrant ainsi une interaction fondamentale entre ces deux types d’endomorphismes dans les espaces vectoriels. Examinons cette relation à travers quelques démonstrations.
1. De projecteur à symétrie : Supposons que \( P \) soit un projecteur, c’est-à-dire \( P^2 = P \). Considérons l’endomorphisme \( S = 2P – I \). Pour vérifier que \( S \) est une symétrie, calculons \( S^2 \):
\[
S^2 = (2P – I)^2 = 4P^2 – 4P + I = 4P – 4P + I = I,
\]
car \( P^2 = P \). Ainsi, \( S \) est bien une symétrie puisqu’elle satisfait à la propriété \( S^2 = I \).
2. De symétrie à projecteurs : Inversement, supposons que \( S \) soit une symétrie, donc \( S^2 = I \). Nous pouvons construire deux projecteurs à partir de \( S \) en utilisant les formules \( \frac{1}{2}(I + S) \) et \( \frac{1}{2}(I – S) \). Démontrons que \( \frac{1}{2}(I + S) \) est un projecteur :
\[
\left(\frac{1}{2}(I + S)\right)^2 = \frac{1}{4}(I + 2S + S^2) = \frac{1}{4}(I + 2S + I) = \frac{1}{2}(I + S).
\]
Cette expression confirme que \( \frac{1}{2}(I + S) \) est un projecteur car elle remplit la condition \( P^2 = P \). De manière similaire, on peut montrer que \( \frac{1}{2}(I – S) \) est aussi un projecteur.
Ces transformations montrent que chaque symétrie peut être décomposée en deux projecteurs qui projettent sur les sous-espaces propres associés aux valeurs propres \( +1 \) et \( -1 \) de \( S \). Ces projecteurs et symétries révèlent la structure sous-jacente des espaces vectoriels et enrichissent notre compréhension des transformations linéaires.
Conclusion
Les notions de projecteurs et de symétries, malgré leur abstraction, offrent des perspectives enrichissantes pour l’analyse des transformations linéaires dans les espaces vectoriels. Les propriétés avancées exposées ici permettent non seulement de mieux comprendre la structure sous-jacente de ces espaces mais aussi d’élargir les outils disponibles pour les mathématiciens dans leur quête de résolution de problèmes. En se familiarisant avec ces concepts, on peut approcher les équations linéaires et les transformations de manière plus intuitive et profonde.
Pour t’entrainer à manipuler les projecteurs et les symétries tu peux réaliser les sujets mathématiques approfondies suivants :
Tu peux retrouver le méga répertoire qui contient toutes les annales de concours et leur corrigé ! Tu peux également accéder à toutes nos autres ressources mathématiques !