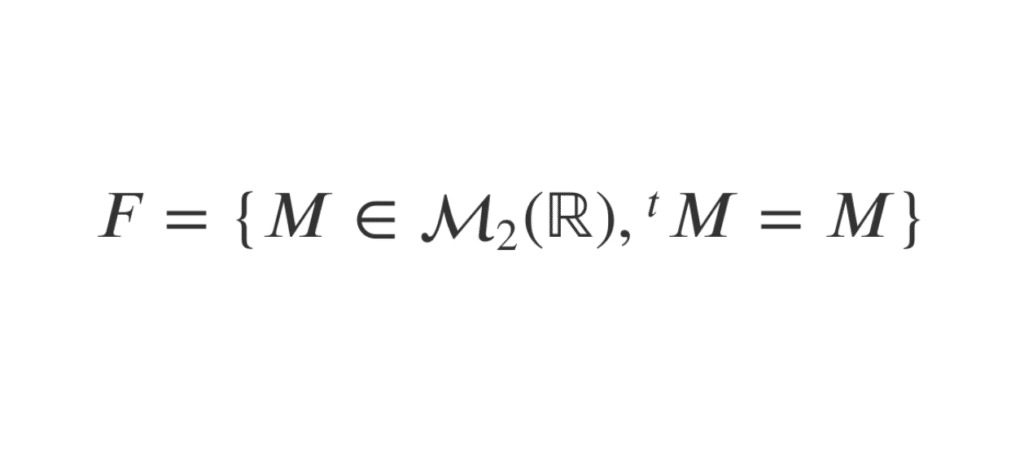Le grand moment de ta première année de prépa est enfin arrivé : l’introduction à la notion d’espaces vectoriels ! Ce chapitre ouvrant la voie à toute l’algèbre linéaire est absolument fondamental. Il est donc important de se confronter à ce chapitre rapidement pour ne pas être noyé en deuxième année.
Dans cet article, tu trouveras des explications sur ce que sont les espaces vectoriels, mais aussi quelques méthodes et astuces concernant ces derniers.
Pourquoi la notion d’espaces vectoriels peut sembler complexe ?
Le chapitre sur les espaces vectoriels marque un passage important et diffère de tout ce que tu as pu faire en mathématiques depuis le début de ta scolarité. La première difficulté est naturellement la nouveauté.
Mais surtout, le plus grand obstacle à la compréhension de ce chapitre, c’est son caractère abstrait. Il y aura très peu de calculs à faire, mais les raisonnements seront plus fins, les objets manipulés plus flous. Pour cela, tu devras toujours t’appuyer sur ton cours, qu’il faudra maîtriser sur le bout des doigts, plus que pour n’importe quel autre chapitre.
Qu’est-ce qu’un espace vectoriel ?
Définir un espace vectoriel rigoureusement est très compliqué. Tu peux te référer à ton cours : c’est un ensemble qui vérifie certaines propriétés. Il y a une dizaine de points à vérifier. Fort heureusement, on ne te demandera jamais de passer par ces points. En effet, d’après le cours, nous avons des espaces vectoriels de référence (par exemple : l’ensemble des polynômes ou l’ensemble des matrices carrées de format \(n\)…).
Mais en vulgarisant, on peut dire qu’un espace vectoriel est un ensemble d’éléments, appelés vecteurs, qui vérifie une loi de stabilité interne et une loi de stabilité externe (nous aurons l’occasion de développer ces notions plus tard). Un espace vectoriel est donc un ensemble avec une infinité d’éléments.
Montrer qu’un ensemble est un espace vectoriel
Il y a globalement deux méthodes pour prouver qu’un ensemble est un espace vectoriel. Pour illustrer, nous allons utiliser l’ensemble suivant : \( F= \{ M \in \mathcal{M}_2(\mathbb{R}), {}^tM=M \} \), qui est, tu l’auras peut-être compris, l’ensemble des matrices carrées \(2 \times 2\) symétriques.
La méthode générale
Cette méthode s’appuie sur la définition simplifiée que j’ai donnée plus tôt : le respect de la loi de stabilité interne et externe.
Comme expliqué précédemment, on ne te demandera pas de montrer que l’ensemble en question vérifie la dizaine de points. On s’appuiera ici sur les espaces vectoriels de référence fournis par le cours. Pour montrer que \(F\) est un espace vectoriel, on montrera que c’est un sous-espace vectoriel d’un espace vectoriel de référence (un sous-espace vectoriel de l’espace vectoriel \(E\) étant un espace vectoriel inclus dans \(E\)).
Dès lors, dans cette méthode, il suffira de vérifier deux points :
- que l’ensemble en question est bien inclus dans un espace vectoriel de référence.
Pour notre exemple, \(F\) est par définition un ensemble de matrices de \(\mathcal{M}_2(\mathbb{R})\), et est donc bien inclus dans cet ensemble qui est un espace vectoriel de référence.
Cette étape peut paraître futile, mais elle témoigne d’une connaissance précise du cours. Je t’encourage fortement à ne pas la sauter.
Sur ta copie, tu pourras simplement écrire que \(F\) est inclus dans \(\mathcal{M}_2(\mathbb{R})\) par définition.
- que toute combinaison linéaire d’éléments de l’ensemble fait toujours partie de l’ensemble.
C’est là le cœur de la démonstration : on s’assure ici du respect de la loi de stabilité interne et externe.
Soit \((M_1, M_2) \in F^2 \). Soit \( \lambda \in \mathbb{R}\). Il s’agit de montrer que \(\lambda M_1 + M_2 \in F\), autrement dit, dans notre cas, que \( \lambda M_1 + M_2 \) est symétrique.
En se souvenant qu’une matrice est symétrique si et seulement si elle est égale à sa transposée, on a :
\({}^t(\lambda M_1 + M_2)= \lambda {}^tM_1 + {}^tM_2= \lambda M_1 + M_2 \), car \(M_1\) et \(M_2\) sont symétriques.
Dès lors, \(\lambda M_1 + M_2 \in F\).
Conclusion
Après avoir vérifié ces deux points, tu peux conclure : \(F\) est un sous-espace vectoriel de \(\mathcal{M}_2(\mathbb{R})\), et est donc un espace vectoriel.
Trouver une famille génératrice
Avant d’utiliser cette méthode pour montrer que \(F\) est bien un espace vectoriel, commençons par expliquer ce qu’est une famille génératrice.
On l’a vu, tout espace vectoriel possède une infinité d’éléments. Pour autant, cela ne signifie pas que les éléments de l’espace vectoriel en question ne se ressemblent pas. On peut en effet « résumer » l’espace vectoriel, c’est à ça que sert une famille génératrice.
Une famille génératrice d’un espace vectoriel est une famille de vecteurs telle que n’importe quel élément de l’espace vectoriel en question peut être exprimé comme une combinaison de ces vecteurs. On écrira alors : \(F=Vect (e_1, \dots, e_p) \), où \((e_1, \dots, e_p) \) est la famille génératrice.
En fait, la notation « Vect » sous-entend déjà que l’ensemble en question est un espace vectoriel. Dans cette méthode, on cherchera donc à exprimer notre ensemble sous la forme d’un « Vect ».
Reprenons notre exemple : \( F= \{ M \in \mathcal{M}_2(\mathbb{R}), {}^tM=M \} \).
En modifiant un peu et en notant \(M=\begin{pmatrix} a & b \\ c & d\end{pmatrix}\), on a \(F=\{ \begin{pmatrix} a & b \\ c& d\end{pmatrix}=\begin{pmatrix} a & c \\ b & d\end{pmatrix},(a,b,c,d)\in \mathbb{R}^4\}\).
Cela signifie donc que \(b=c\).
Ainsi, on a \( F=\{\begin{pmatrix} a & b \\ b& d\end{pmatrix}, (a,b,d) \in \mathbb{R}^3\}\).
Dit autrement : \( F= \{ a \times \begin{pmatrix} 1 & 0 \\ 0 & 0\end{pmatrix} + b \times \begin{pmatrix} 0 & 1 \\ 1 & 0\end{pmatrix} + d \times \begin{pmatrix} 0 & 0 \\ 0 & 1\end{pmatrix}, (a,b,d) \in \mathbb{R} \} \).
C’est exactement la définition de \(F= Vect (\begin{pmatrix} 1 & 0 \\ 0 & 0\end{pmatrix}, \begin{pmatrix} 0 & 1 \\ 1 & 0\end{pmatrix} \begin{pmatrix} 0 & 0 \\ 0 & 1\end{pmatrix} ) \).
Dès lors que l’on a exprimé \(F\) sous la forme d’un « Vect », on peut conclure : \(F\) est un espace vectoriel.
Que retenir de ces démonstrations ?
Ces deux démonstrations aboutissent à la même conclusion. Toutefois, il y a une nuance importante. La deuxième démonstration, en plus d’être plus courte, fournit plus d’informations, puisqu’elle nous donne une famille génératrice de l’espace vectoriel.
Ainsi, si tu te retrouves dans une situation où tu penses pouvoir utiliser les deux méthodes, il serait plus judicieux de choisir la deuxième.
Toutefois, il s’avère parfois difficile, voire tout bonnement impossible, de donner une famille génératrice d’un ensemble qui est pourtant bien un espace vectoriel. Le cas des espaces vectoriels de fonctions est un parfait exemple. Dans ce cas, la première méthode est la seule adéquate.
Alors comment choisir entre ces deux méthodes ?
Si la question posée dans le sujet est « Montrer que \(F\) est un espace vectoriel, et en donner une base/une famille génératrice », tu peux être sûr·e de toi et foncer sur la deuxième méthode.
Si la question est juste « Montrer que \(F\) est un espace vectoriel », la première méthode, qui marche dans tous les cas, est sûrement la plus appropriée.
Conclusion
Savoir montrer rigoureusement qu’un ensemble est un espace vectoriel est fondamental pour toute la suite du cours d’algèbre linéaire. C’est sur ce fondement que tu t’appuieras pour parler de base, de dimension, et plus tard d’applications linéaires.
N’hésite pas à consulter toutes nos autres ressources mathématiques !