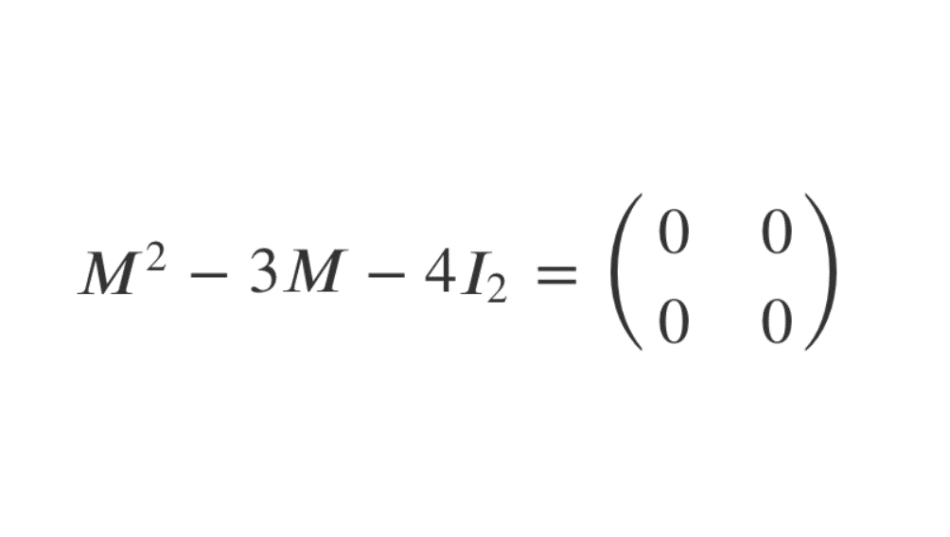Les notions hors programme se retrouvent très souvent dans les sujets de mathématiques pour les trois Parisiennes. Cet article te propose donc de décrypter la notion du polynôme minimal d’un endomorphisme, à l’aide d’exemples concrets.
Une liste des propriétés associées est également présente afin de t’aider à appréhender au mieux cette notion hors programme quand tu la rencontreras au cours d’un exercice !
La notion de polynôme minimal d’un endomorphisme expliquée en français
Le polynôme minimal d’un endomorphisme est un polynôme unitaire (c’est-à-dire avec le coefficient 1 devant son terme de plus haut degré) qui annule cet endomorphisme, tout en étant de plus petit degré possible.
Si les polynômes \(X^2+4\) et \(X-1\) annulent un endomorphisme \(f\) par exemple, et qu’aucun polynôme de degré 0 ne peut annuler \(f\), alors le polynôme minimal de l’endomorphisme \(f\) est donc le polynôme \(X-1\) (qui est seulement de degré 1, contrairement au polynôme \(X^2+4\) qui est lui de degré 2).
Exemple concret
Prenons l’endomorphisme \(u\) appartenant à l’espace vectoriel réel \(E\) de dimension 2. Posons \(M=\begin{pmatrix} 1 & 3 \\ 2 & 2\end{pmatrix}\), la matrice associée à \(u\) dans la base \((e_1,e_2)\).
On calcule alors \(M^2=\begin{pmatrix} 7 & 9 \\ 6 & 10\end{pmatrix}\).
On peut alors voir que \(M^2-3M-4I_{2}=\begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}\).
Ainsi, le polynôme \(P=X^2-3X-4=(X+1)(X-4)\) est un polynôme annulateur de l’endomorphisme \(u\). Comme il n’existe pas de relation linéaire possible entre \(M\) et \(I_2\) qui pourrait donner la matrice nulle, on peut alors conclure que \(P\) est le polynôme minimal de \(u\) (qui est toujours de degré égal ou inférieur à la dimension de l’espace vectoriel de l’endomorphisme, et ici \(E\) est de dimension 2).
Définition mathématique du polynôme minimal d’un endomorphisme
Soit \(E\) un espace vectoriel de dimension finie \(n\) et \(u\) un endomorphisme de \(E\). Le polynôme unitaire de \(u\) est alors le polynôme unitaire de plus petit degré possible qui annule \(u\).
La notion de polynôme unitaire est surtout utilisée en dimension finie (même si elle existe également en dimension infinie).
Quelques propriétés liées au polynôme minimal d’un endomorphisme
Soit \(u\) un endomorphisme dans l’espace vectoriel \(E\) de dimension finie égale à \(n\) et \(M\) la matrice canoniquement associée à \(u\). Soit \(P\) le polynôme minimal de \(u\).
- Quand l’espace vectoriel de l’endomorphisme est de dimension finie, alors il existe toujours un polynôme minimal, qui est de degré égal ou inférieur à la dimension de cet espace vectoriel (donc ici avec nos notations, \(deg(P)\le n\)).
- Les racines de \(P\) sont les valeurs propres de l’endomorphisme \(u\).
- L’endomorphisme \(u\) est diagonalisable si et seulement si \(P\) est produit de polynôme de degré 1 et si toutes ses racines sont réelles (c’est-à-dire de la forme \(\displaystyle \sum_{k=1}^{p}(X-a_k)\) , avec \(p\le n\), les \(a_k\) étant les racines du polynôme, qui doivent être toutes réelles et non complexes).
- Le théorème de Cayley-Hamilton montre que le polynôme minimal \(P\) de l’endomorphisme \(u\) divise le polynôme caractéristique de \(u\).
Méthode pour appliquer ces propriétés avec l’endomorphisme \(u\) de l’exemple
Reprenons l’endomorphisme \(u\) appartenant à l’espace vectoriel réel \(E\) de dimension 2. Posons \(M=\begin{pmatrix} 1 & 3 \\ 2 & 2\end{pmatrix}\), la matrice associée à \(u\) dans la base \((e_1,e_2)\). Nous avons déterminé que \(P=(X+1)(X-4)\) était son polynôme minimal.
Trouver les valeurs et vecteurs propres de l’endomorphisme \(u\) grâce au polynôme minimal \(P\)
Toute racine de \(P\) est alors valeur propre de l’endomorphisme \(u\) d’après les propriétés annoncées plus haut. Ainsi, nous pouvons affirmer d’après \(P\) que \(Sp(u)=\{-1,4\}\).
Il ne reste plus qu’à résoudre un système pour trouver les vecteurs propres \(u_1\) et \(u_2\). \(u_1\), le vecteur propre associé à la valeur propre –1 vérifie le système suivant : \[\begin{cases} x+3y=-x \\ 2x+2y=-y\end{cases} \Leftrightarrow 2x+3y=0\]
Ainsi, un vecteur propre qui convient est alors \(u_1=3e_1-2e_2\), c’est-à-dire \((3;-2)\).
De la même manière, on obtient que \(u_2=e_1+e_2\), c’est-à-dire \((1,1)\).
Cette méthode est surtout utile, car elle permet de ne pas calculer le déterminant des matrices (ce qui est avantageux quand la dimension augmente).
Diagonaliser la matrice \(M\) grâce au polynôme minimal \(P\)
\(u_1\) et \(u_2\) sont donc deux vecteurs propres de notre endomorphisme \(u\). On peut alors remarquer que l’expression de \(u\) dans la base \((e_1,e_2)\) donne alors une matrice diagonale, ici égale à \(\begin{pmatrix} -1 & 0 \\ 0 & 4\end{pmatrix}\).
L’endomorphisme est donc diagonalisable si et seulement si le polynôme minimal ne possède que des racines simples.
Calculer le polynôme caractéristique de \(u\) en partant du polynôme minimal \(P\)
On appelle polynôme caractéristique, que l’on note \(Q\), de l’endomorphisme \(u\), le déterminant de l’endomorphisme \(XId-u\). Comme le polynôme minimal \(P\), ses racines sont les valeurs propres de \(u\).
Ainsi, en se souvenant que \(u\) avait une matrice associée \(M=\begin{pmatrix} 1 & 3 \\ 2 & 2\end{pmatrix}\) dans la base \((e_1,e_2)\), on peut calculer le déterminant de l’endomorphisme \(XId-u\) et trouver alors que \[Q(X)=(X-1)(X-2)-3\times 2=X^2-3X+2-6=X^2-3X-4=P(X)\]
Ici, \(P(X)=Q(X)\), c’est-à-dire que le polynôme minimal est égal au polynôme caractéristique de l’endomorphisme \(u\), mais l’égalité n’est pas toujours vraie (on sait cependant d’après le théorème de Cayley-Hamilton expliqué plus haut que \(P\) divise toujours \(Q\)).
Sujet de concours avec cette notion
Cette notion s’est retrouvée dans plusieurs sujets de concours, en voici un pour que tu puisses t’entraîner : HEC 2009.