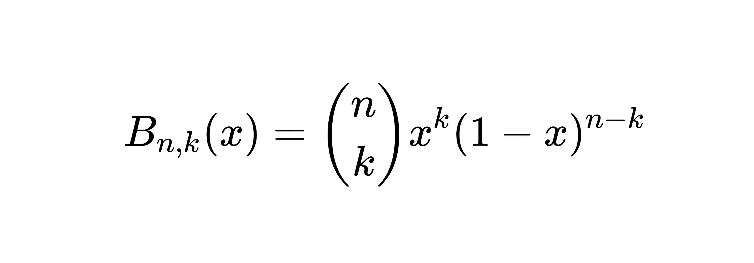Dans cet article, tu découvriras les polynômes de Bernstein, une famille de polynômes très intéressante à étudier, notamment liée aux convergences en loi. Ces polynômes sont déjà tombés aux écrits en maths approfondies ainsi qu’aux oraux de HEC, et sont amenés à retomber à l’avenir !
Les polynômes de Berstein expliqués en mathématiques
Définition
On définit les polynômes de Bernstein par :
\[\forall n \in\mathbb{N} , \forall k \in [\![0,n]\!], B_{n,k} (x) = {{n}\choose{k}}x^k(1-x)^{n-k}\]
Premiers exemples
On a donc les premiers polynômes de Bernstein qui sont définis par :
\(n=0\) : \(B_{0,0} = 1\)
\(n=1\) : \(B_{1,0} = 1-x , B_{1,1} = x\)
\(n=2\) : \(B_{2,0} = (1-x)^2, B_{2,1} = 2x(1-x) , B_{2,2} = x^2\)
Propriétés des polynômes de Bernstein
Les polynômes de Bernstein possèdent un très grand nombre de propriétés intéressantes. Il sera ici question des propriétés des polynômes en analyse, puis en algèbre et enfin en probabilités.
Étude des polynômes (analyse)
Avant tout, les polynômes de Bernstein s’étudient en général non pas sur \(\mathbb{R}\), mais plutôt sur \([0,1]\). Les propriétés énoncées seront donc valables sur \([0,1]\).
Degré de \(B_{n,k}\)
Il peut d’abord être intéressant de déterminer le degré de \(B_{n,k}\). On a alors la propriété suivante :
\[\forall n \in
\mathbb{N} , \forall k \in [\!
[0,n]\!],deg( B_{n,k}) = n\]
La démonstration est assez rapide. Indice : Tu peux utiliser la formule du binôme de Newton pour décomposer \((1-x)^{n-k}\).
Partitions de l’unité
D’après ce même binôme de Newton, il est immédiat que l’on a la propriété suivante :
\[\forall n \in
\mathbb{N} , \displaystyle \sum_{k=0}^{n}B_{n,k} = 1\]
Racines et ordre de multiplicité des racines de \(B_{n,k}\)
Il est également possible d’étudier les racines de ces polynômes et même leur ordre de multiplicité. On obtient alors le résultat suivant :
\(\forall n \in\mathbb{N^{*}} , \forall k \in [\![1,n]\!],B_{n,k}\)a pour racines \(0\) et \(1\), \(0\) étant une racine de multiplicité \(k\) et \(1\) une racine de multiplicité \(n-k\).
Formule de symétrie
\[\forall n \in
\mathbb{N} , \forall k \in [\!
[0,n]\!], \forall x \in [0,1], B_{n,k}(x) = B_{n,n-k}(1-x) \]
La démonstration de cette formule est assez rapide et offre une petite révision des formules sur les coefficients binomiaux, réalisons-la.
Démonstration
Soit \(n \in\mathbb{N} , k \in [\![0,n]\!] , \)
\(\displaystyle B_{n,n-k}(1-x) = {{n}\choose{n-k}}(1-x)^{n-k}(1-(1-x))^{n-(k-k)}\)
Et d’après la formule de symétrie des coefficients binomiaux, on sait que \(\displaystyle {{n}\choose{n-k}} = {{n}\choose{k}}\). Ainsi,
\(\displaystyle B_{n,n-k}(1-x) = {{n}\choose{k}}(1-x)^{n-k}(x)^k = B_{n,k}(x) \) \(CQFD\)
Expression de la dérivée
Comme tout polynôme, \(B_{n,k}(x)\) est dérivable sur \([0,1]\). Savoir exprimer sa dérivée en fonction des polynômes de la même famille est une question de base qui revient souvent dans les sujets de type EDHEC/Emlyon. Voici la formule que l’on obtient :
\[\forall n \in
\mathbb{N^{*}} , \forall k \in [\!
[1,n]\!], \forall x \in [0,1], B_{n,k}^{‘}(x) = n(B_{n-1,k-1}(x) – B_{n-1,k}(x)) \]
Je te laisse essayer de démontrer ce résultat. Si tu as des difficultés, tu peux essayer de partir du côté gauche de l’égalité, la travailler, puis partir du côté droit pour essayer de trouver un résultat égal à celui trouvé du côté gauche. Attention à la gestion des coefficients binomiaux et pense aux formules de cours sur ces derniers.
Liens en algèbre linéaire
Partitions de l’unité
Avec la première propriété démontrée précédemment, on dit que les polynômes \(B_{n,k}\) de la famille \((B_{n,k})_{k \in [\!
[0,n]\!]}\) forment une partition de l’unité. En effet, par définition, on dit qu’une partition de l’unité est une famille de fonctions positives \((\delta_i)_{i \in I}\) définie sur un intervalle \(D\) tel que \(\displaystyle \forall x \in D, \sum_{i \in {I}}{} (\delta_i)(x) = 1\).
Exemple :
Cette propriété se voit très bien graphiquement avec la famille \((B_{2,k})_{k \in [\!
[0,2]\!]}\). Voici le graphique des trois polynômes sur l’intervalle \([0,1]\) :
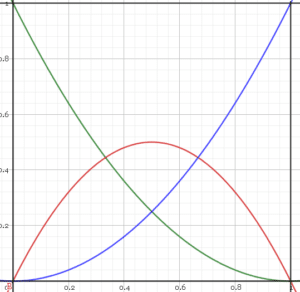
Il suffit de sommer les trois courbes pour remarquer que leur somme est toujours égale à 1.
Décomposition dans la base canonique
Soit \(B = (1,x,… x^n)\) la base canonique de \(R_n[x]\). Alors il est possible de décomposer \(B_{n,k}\) dans \(B\). La formule est alors la suivante :
\[\forall n \in
\mathbb{N^{*}} , \forall k \in [\!
[1,n]\!], \forall x \in [0,1], B_{n,k}(x) = {{n}\choose{k}}\displaystyle \sum_{i=0}^{n-k}{{n-k}\choose{i}}(-1)^{i}x^{k+i} = \displaystyle \sum_{l=k}^{n}{{n}\choose{l}}{{l}\choose{k}}(-1)^{l-k}x^{l}\]
Démontrons rapidement le passage entre les deux dernières égalités. La démonstration est intéressante, car elle fait appel à la gestion, récurrente aux écrits, des doubles coefficients binomiaux.
Démonstration
Procédons avec le changement de variable \(l = k+i\), on a donc :
\( B_{n,k}(x) = {{n}\choose{k}}\displaystyle \sum_{i=0}^{n-k}{{n-k}\choose{i}}(-1)^{i}x^{k+i} = \displaystyle \sum_{l=k}^{n}{{n}\choose{k}}{{n-k}\choose{l-k}}(-1)^{l-k}x^{l}\).
Il reste ensuite à gérer les coefficients binomiaux. On décompose alors tout ça !
\(\displaystyle {{n}\choose{k}}{{n-k}\choose{l-k}} = \frac{n!}{k!(n-k)!} \frac{(n-k)!}{(l-k)!(n-k-(l-k))!} = \frac{n!}{k!} \frac{1}{(l-k)!(n-l)!} = \frac{n!}{k!} \frac{1}{(l-k)!(n-l)!} \frac{l!}{l!} = \frac{l!}{k!(l-k)!} \frac{n!}{l!(n-l)!} = {{l}\choose{k}}{{n}\choose{l}}\)
Et voilà, on retrouve donc bien la seconde formule possible de décomposition des polynômes de Bernstein dans \(B\).
À partir de cette décomposition dans la base canonique, on peut aisément déterminer la matrice représentative de \(B_{n,k}\) dans la base \(B\) !
Une base de \(R_n [x]\)
\(\forall n \in\mathbb{N}\), la famille \({(B_{n,k})}_{k \in[\![0,n]\!]}\) forme une base de \(R_n [x]\).
Pour la démonstration, il y a juste à montrer que cette famille est libre puisqu’il y a déjà n + 1 éléments de \(R_n [x]\) dans cette famille (cf. degré de \({B_{n,k}}\)). La démonstration est plutôt longue. Indice : Pense à évaluer les polynômes à leurs racines, c’est-à-dire en 0 et 1.
Liens avec les probabilités
Voilà la partie qui est sûrement la plus intéressante avec les polynômes de Bernstein. Il est en effet rare de lier des polynômes avec des probabilités dans le programme d’ECG, et pourtant ces polynômes permettent cela !
Pour établir des propriétés intéressantes en probabilités avec les polynômes de Bernstein, on définit les « polynômes de Bernstein associés à une fonction ». Les polynômes de Bernstein associés à \(f\) sont définis par :
\[\forall n \in
\mathbb{N}, B_{n}(f) (x) =\displaystyle \sum_{k=0}^{n} f(\frac{k}{n}){{n}\choose{k}}x^k(1-x)^{n-k}\]
On considère pour le reste de l’article une suite de variables aléatoire\(X_1,…., X_n\) mutuellement indépendantes suivant toutes une loi de Bernoulli de paramètre \(p\), où \(p \in [0,1]\).
On pose alors : \(\displaystyle \forall n \in \mathbb{N}, S_n = \frac{X_1 + … + X_n}{n}\)
Théorème de transfert
D’après le théorème de transfert, on a directement l’égalité suivante :
\(E(S_n) = B_n(f)\)
Théorème de Weierstrass
Les polynômes de Bernstein permettent également de démontrer un résultat immense en analyse : le théorème de Weierstrass (complètement hors programme). Ce dernier stipule que « toute fonction continue sur un intervalle fermé peut-être approché aussi précisément que voulu par une fonction polynomiale ».
Aperçu de la preuve : Avec les outils disponibles dans le programme d’ECG, on peut démontrer que :
\(\forall n \in\mathbb{N}, \exists (K, \alpha) \in \mathbb{R}\times[0,1]\) tel que \( \displaystyle \forall x \in[0,1], |f(x)-B_n(f)(x)| \le \frac{3K}{2} \frac{1}{n^{\frac{\alpha}{2}}}\)
Le sujet numéro 16 de l’oral de HEC 2023 de mathématiques approfondies s’attache justement à démontrer une telle inégalité ! Démonstration technique donc… mais pas impossible !
À partir d’une telle inégalité, on remarque que \(\displaystyle \lim \limits_{n \to +\infty} \frac{3K}{2} \frac{1}{n^{\frac{\alpha}{2}}} = 0 \) et donc par encadrement que \(\lim \limits_{n \to +\infty} f(x)-B_n(f)(x) = 0\). Autrement dit :
\[\forall x \in[0,1], \lim \limits_{n \to +\infty}B_n(f)(x) = f(x)\]
Ceci achève de prouver le théorème de Weierstrass ! En effet, lorsque n devient très grand, le polynôme de Bernstein associé à \(f\) permet d’approcher très précisément \(f\) (puisque quand n tend vers \(+\infty\), l’écart entre \(f\) et \(B_n(f)\) tend vers \(0\)).
Convergence en probabilité
À l’aide de l’inégalité de Markov, on peut démontrer la convergence en probabilité suivante (qui découle en fait du théorème de Weierstrass) :
\[E(S_n(f))\overset{\mathbb{P}} {\rightarrow} E(f(x)) = f(x)\]
Conclusion
En définitive, les polynômes de Bernstein permettent d’aborder dans un même sujet un grand nombre de notions du programme d’ECG. C’est donc un sujet idéal pour une Maths I ! En témoigne le fait qu’un tel sujet est déjà tombé lors de la Maths I HEC de 2017. S’exercer sur cette famille de polynômes permet de vérifier sa maîtrise d’une grande partie du programme de mathématiques. Il n’y a plus qu’à croiser les doigts pour qu’un tel sujet retombe aux concours !
Tu peux retrouver le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder à toutes nos autres ressources mathématiques !