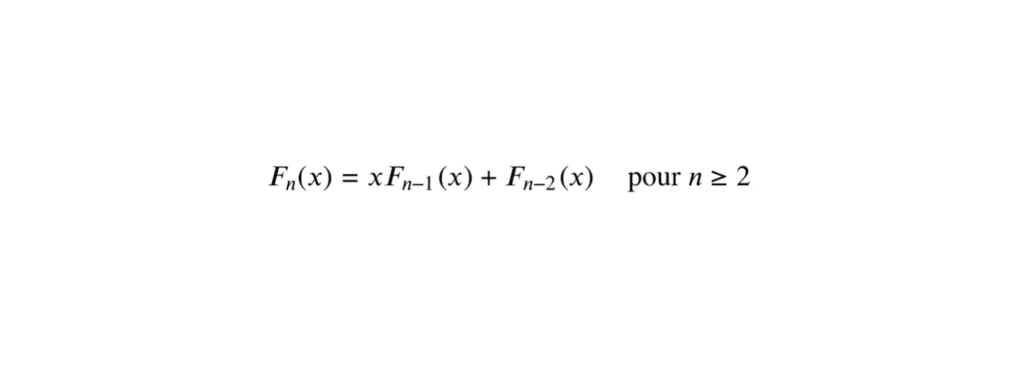Les polynômes de Fibonacci constituent une extension naturelle et fascinante de la célèbre suite de Fibonacci (que l’on doit au mathématicien Leonardo Fibonacci, inventeur du nombre d’or), largement étudiée pour ses nombreuses propriétés mathématiques et ses apparitions dans des contextes variés tels que la nature, l’art et la science. En passant des nombres à des polynômes, on ouvre la porte à une exploration plus profonde et plus abstraite de ces structures récurrentes. Cette généralisation permet non seulement de redécouvrir des propriétés bien connues sous une nouvelle forme, mais aussi de dévoiler de nouvelles connexions avec d’autres domaines des mathématiques, notamment l’algèbre, la théorie des nombres et les polynômes orthogonaux. Cet article explore les définitions, les propriétés et les applications des polynômes de Fibonacci, en mettant en lumière leur richesse et leur utilité dans divers contextes mathématiques.
Les polynômes de Fibonacci
Les polynômes de Fibonacci sont une généralisation des célèbres nombres de Fibonacci, qui sont définis par la récurrence simple \( F_n = F_{n-1} + F_{n-2} \) avec les conditions initiales \( F_0 = 0 \) et \( F_1 = 1 \). Dans le cadre des polynômes de Fibonacci, cette récurrence est étendue aux polynômes en une variable \(x\), ce qui introduit des propriétés intéressantes et des applications diverses en mathématiques.
Rigoureusement, les polynômes de Fibonacci \( F_n(x) \) sont définis de manière récurrente comme suit :
\[
F_0(x) = 0, \quad F_1(x) = 1,
\]
\[
F_n(x) = xF_{n-1}(x) + F_{n-2}(x) \quad \text{pour } n \geq 2.
\]
Cette relation montre que chaque polynôme de Fibonacci est une combinaison linéaire des deux polynômes précédents, pondérés par les coefficients \( x \) et \( 1 \).
Exemples de polynômes de Fibonacci
Calculons les premiers polynômes de Fibonacci pour illustrer la définition :
\[
\begin{aligned}
F_2(x) & = xF_1(x) + F_0(x) = x \cdot 1 + 0 = x, \\
F_3(x) & = xF_2(x) + F_1(x) = x \cdot x + 1 = x^2 + 1, \\
F_4(x) & = xF_3(x) + F_2(x) = x(x^2 + 1) + x = x^3 + x + x = x^3 + 2x, \\
F_5(x) & = xF_4(x) + F_3(x) = x(x^3 + 2x) + (x^2 + 1) = x^4 + 2x^2 + x^2 + 1 = x^4 + 3x^2 + 1.
\end{aligned}
\]
Ainsi, les premiers polynômes de Fibonacci sont :
\[
\begin{aligned}
F_0(x) & = 0, \\
F_1(x) & = 1, \\
F_2(x) & = x, \\
F_3(x) & = x^2 + 1, \\
F_4(x) & = x^3 + 2x, \\
F_5(x) & = x^4 + 3x^2 + 1.
\end{aligned}
\]
Propriétés des polynômes de Fibonacci
Les polynômes de Fibonacci, tout comme les nombres de Fibonacci, possèdent de nombreuses propriétés intéressantes qui permettent de les étendre, de les relier à d’autres suites et d’explorer des comportements complexes.
Relation de récurrence
Les polynômes de Fibonacci vérifient une relation de récurrence d’ordre 2 similaire à celle des nombres de Fibonacci :
\[
F_n(x) = xF_{n-1}(x) + F_{n-2}(x).
\]
Cette relation peut être étendue pour produire des expressions plus complexes.
Expression en fonction des racines
Les polynômes de Fibonacci peuvent être exprimés en termes des racines de l’équation caractéristique associée à leur récurrence :
\[
F_n(x) = \frac{\alpha(x)^n – \beta(x)^n}{\alpha(x) – \beta(x)},
\]
où \( \alpha(x) \) et \( \beta(x) \) sont les solutions de l’équation quadratique :
\[
t^2 – xt – 1 = 0.
\]
Ces solutions sont données par :
\[
\alpha(x) = \frac{x + \sqrt{x^2 + 4}}{2}, \quad \beta(x) = \frac{x – \sqrt{x^2 + 4}}{2}.
\]
Relation avec les polynômes de Lucas
Les polynômes de Fibonacci sont reliés aux polynômes de Lucas par la relation :
\[
F_{2n}(x) = F_n(x) L_n(x),
\]
où \( L_n(x) \) représente le polynôme de Lucas correspondant.
Les polynômes de Lucas sont bien évidemment liés à la suite de Lucas.
Relations récurrentes généralisées
Pour tout entier \( m \) et \( n \), les polynômes de Fibonacci satisfont une relation récurrente généralisée :
\[
F_{m+n}(x) = F_{m+1}(x)F_n(x) + F_m(x)F_{n-1}(x).
\]
Quant aux polynômes de Lucas, ils satisfont la relation suivante :
\[
L_{m+n}(x) = L_m(x)L_n(x) – (-1)^nL_{m-n}(x).
\]
Identité de Cassini
Les polynômes de Fibonacci vérifient également une identité analogue à celle de Cassini pour les nombres de Fibonacci :
\[
F_{n+1}(x)F_{n-1}(x) – F_n(x)^2 = (-1)^n.
\]
Définition pour les indices négatifs
Les polynômes de Fibonacci et de Lucas peuvent être étendus aux indices négatifs par les relations :
\[
F_{-n}(x) = (-1)^{n-1}F_n(x), \quad L_{-n}(x) = (-1)^nL_n(x).
\]
Ces extensions permettent de définir ces polynômes de manière cohérente pour tout entier \( n \).
Somme des coefficients
La somme des coefficients d’un polynôme de Fibonacci est égale au nombre de Fibonacci correspondant :
\[
F_n(1) = F_n.
\]
Cela montre que les polynômes de Fibonacci généralisent les nombres de Fibonacci en introduisant un paramètre supplémentaire \( x \), tout en conservant des propriétés similaires.
Relation avec les polynômes de Tchebychev
Enfin, les polynômes de Fibonacci sont également liés aux polynômes de Tchebychev \( T_n(x) \) par la relation :
\[
F_n(2x) = T_n(x).
\]
Cela montre une connexion directe entre ces deux importantes familles de polynômes.
Polynômes de Fibonacci et algèbre linéaire
Les polynômes de Fibonacci jouent un rôle important en algèbre linéaire, notamment dans l’expression des puissances d’un monôme \(x^n\) en tant que combinaison linéaire des polynômes de Fibonacci. En effet, pour tout entier \(n \geq 1\), il est possible de représenter \(x^n\) à l’aide de la formule suivante :
\[
x^n = F_{n+1}(x) + \sum_{k=1}^{\left\lfloor n/2 \right\rfloor} (-1)^k \left[ \binom{n}{k} – \binom{n}{k-1} \right] F_{n+1-2k}(x).
\]
Cette formule montre que chaque puissance de \(x\) peut être décomposée en une combinaison de polynômes de Fibonacci de degrés inférieurs. Par exemple :
\[
\begin{aligned}
x^4 & = F_5(x) – 3F_3(x) + 2F_1(x), \\
x^5 & = F_6(x) – 4F_4(x) + 4F_2(x), \\
x^6 & = F_7(x) – 5F_5(x) + 9F_3(x) – 5F_1(x), \\
x^7 & = F_8(x) – 6F_6(x) + 14F_4(x) – 14F_2(x).
\end{aligned}
\]
Ces relations démontrent comment les puissances successives de \(x\) peuvent être construites à partir des polynômes de Fibonacci, ce qui permet de relier la théorie des polynômes de Fibonacci à l’algèbre linéaire. Cette approche trouve des applications dans l’analyse de suites récurrentes et la résolution de systèmes linéaires, où les propriétés structurelles des polynômes de Fibonacci facilitent la manipulation algébrique et la simplification des expressions.
Polynômes de Fibonacci et combinatoire
Les polynômes de Fibonacci possèdent une interprétation combinatoire riche, qui relie directement leurs coefficients aux pavages de dominos et à la structure du triangle de Pascal. Si \( F(n, k) \) désigne le coefficient de \( x^k \) dans le polynôme de Fibonacci \( F_n(x) \), alors ce coefficient représente le nombre de façons de paver une bande de \( n-1 \) cases à l’aide de dominos \( 2 \times 1 \) et de \( k \) carrés \( 1 \times 1 \).
En d’autres termes, \( F(n, k) \) compte le nombre de façons d’écrire \( n-1 \) comme une somme ordonnée de 1 et de 2, avec exactement \( k \) apparitions de 1. Par exemple, \( F(6, 3) = 4 \), car il existe quatre façons de représenter 5 comme une somme ordonnée de 1 et de 2 avec exactement trois 1 : \( 1+1+1+2 \), \( 1+1+2+1 \), \( 1+2+1+1 \), et \( 2+1+1+1 \).
De plus, les coefficients des polynômes de Fibonacci peuvent être directement calculés à partir du coefficient binomial :
\[
F(n, k) = \binom{\frac{n+k-1}{2}}{k},
\]
où \( n \) et \( k \) doivent être de parité opposée. Cette relation permet de lire les coefficients des polynômes de Fibonacci sur les « diagonales » du triangle de Pascal, ce qui illustre encore plus profondément la connexion entre ces polynômes et les structures combinatoires classiques. Les sommes de ces coefficients à travers les différentes puissances de \( x \) reproduisent alors les nombres de Fibonacci, soulignant l’importance des polynômes de Fibonacci dans l’étude des suites récurrentes et des pavages combinatoires.
À lire également : Les matrices de Fibonacci.
Aller plus loin
La suite de Fibonacci est à l’origine de nombreuses recherches et nombreux problèmes mathématiques. Pour y voir plus clair, voici une cartographie de l’ensemble des recherches tournant autour de la suite de Fibonacci (et du nombre d’or) :
| Tableau de correspondances suites/nombres (en lien avec Fibonacci/nombres métalliques) |
|
| Suites | Nombres |
| Suite de Fibonacci | Nombre d’or |
| Suite de Pell | Nombre d’argent |
| Généralisation de Fibonacci : les suites k-bonacci | Nombres métalliques : généralisation du nombre d’or |
| Suite de Lucas | Nombre de Lucas |
| Suite de Padovan | Nombre plastique |
| Suite de Perrin | Nombres pseudo-premiers de Perrin |
| Suite de Jacobsthal | Nombres oblongs de Jacobsthal |
| Polynôme/suite de Narayana | Nombre de Narayana |
| Nombre de Gildas | |
| Nombre de Keith | |
| Super nombre d’or | |
Un autre type de généralisation de la suite de Fibonacci est également à découvrir ! Il s’agit de la suite de Fibonacci aléatoire. Elle pourrait clairement faire l’objet d’un sujet de maths parisienne dans les années à venir…
A lire également : le triangle de Pascal (et ses liens avec la suite de Fibonacci).
Conclusion
Les polynômes de Fibonacci offrent une généralisation élégante et riche des nombres de Fibonacci, permettant d’explorer de nouvelles propriétés et d’étendre les applications des suites récurrentes. Leurs connexions avec d’autres branches des mathématiques en font un sujet d’étude fascinant, avec des implications profondes dans divers domaines. Ces polynômes illustrent la beauté des généralisations en mathématiques et leur capacité à unifier des concepts apparemment distincts.
Ainsi, bien que les polynômes de Fibonacci soient hors programme, la compréhension approfondie des propriétés liées à ces polynômes te permettra d’améliorer tes compétences en analyse et en algèbre. Ce qui te préparera donc pour les épreuves écrites et orales. Pour t’entraîner sur cette notion, tu peux réaliser les sujets suivants :
- Ecricome 2018 (mathématiques approfondies),
- Maths 1 HEC 2009 (mathématiques appliquées),
- la première Question Sans Préparation des Oraux HEC 2023.
Tu peux retrouver le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder à toutes nos autres ressources mathématiques !