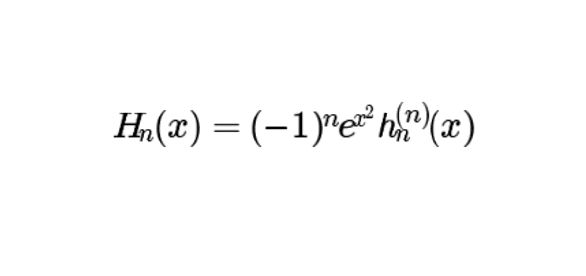Je te présente dans cet article des polynômes hors programme : les polynômes d’Hermite. Cette suite de polynômes a été nommée en l’honneur du mathématicien Charles Hermite. Elle apparaît dans de nombreux champs d’application : physique, analyse numérique, probabiliste, dans le cas de matrices aléatoires… Les possibilités sont nombreuses et il est ainsi probable que les concepteurs de sujets de concours ou d’oraux introduisent un jour ces fameux polynômes. Cet article te présentera donc les propriétés essentielles de ces polynômes. Tu trouveras également des idées de démonstration de certaines de ces propriétés.
L’étude de polynômes particuliers est un exercice récurrent dans les annales, cela peut constituer un exercice pour les épreuves EML/EDHEC ou alors une partie d’un problème pour les annales de Parisiennes. On s’intéresse ici aux polynômes d’Hermite, et cet article vise à décortiquer toutes les questions « classiques » liées à ces polynômes.
Définition des polynômes d’Hermite
La définition la plus courante en mathématiques est la suivante : \[\forall x \in \mathbb{R}, \forall n \in \mathbb{N}, H_n : x \mapsto (-1)^n \phi^{(n)}(x) \times \frac{1}{\phi(x)}\]
On peut également écrire cette suite de fonction sous forme de développement polynomial. Ainsi,
\[\forall x \in \mathbb{R}, \forall n \in \mathbb{N}, H_n(x) = \displaystyle \sum_{k = 0}^{\lfloor \frac{n}{2} \rfloor} (-1)^k \frac{n!}{2^kk!(n – 2k)!}x^{n – 2k}\]
Présentation des polynômes d’Hermite
Les polynômes d’Hermite sont les polynômes \(H_n\) définis pour \(n\) un entier naturel par : \(H_n(x)=(-1)^n e^{x^2}h_n^{(n)}(x)\textrm{ avec }h_n(x)=e^{-x^2}\).
En particulier, on a \( H_0=1\), \(H_1=X\), \(H_2=X^2-1\), \(H_3=X^3-3X\) et \(H_4=X^4-6X^2+3\).
Relations de récurrence entre les polynômes de Hermite
Il existe deux relations de récurrence entre les polynômes d’Hermite :
Première relation de récurrence :
\( \forall n \in \mathbb{N}^*, \forall x \in \mathbb{R}, H_{n + 1}(x) = xH_n(x) – nH_{n – 1}(x)\)
1 – Montrons \(H_{n+1}=XH_n-nH_(n-1)’\) avec \(n\) un entier naturel supérieur ou égal à 2
\(H_{n+1}=(-1)^{n+1}e^{x^2}h_n^{(n+1)}(x)=(-1)^{n+1}e^{x^2}(h_n’)^{(n)}(x)=(-1)^{n+1}e^{x^2}(-xh_n(x))^{(n)}\). En utilisant Leibniz, on trouve \(H_{n+1}=(-1)^{n+1}e^{x^2}(-xh_n^{(n)}(x)-nh_n^{(n-1)}(x)=xH_n(x)-nH_{n-1}(x))\).
Seconde relation de récurrence :
\( \forall n \in \mathbb{N}^*, \forall x \in \mathbb{R}, H_n'(x) = nH_{n – 1}(x)\)
2 – Montrons \(H_n’=nH_{n-1}\) avec \(n\) un entier naturel supérieur ou égal à 1
On peut écrire que \(H_n=\frac{(-1)^n}{h_n}h_n^{(n)}\). D’où \(h_nH_n=(-1)^nh_n^{(n)}\). En dérivant, on trouve alors \(-xh_n(x)H_n(x)+h_n(x)H_n'(x)=(-1)^nh_n^{(n+1)}=-h_nH_{n+1}\). En divisant par \(h_n\) qui est toujours positif, on obtient \(-XH_n+H_n’=-H_{n+1}\). On utilise alors la relation de récurrence montrée au-dessus et on trouve \(-XH_n+H_n’=-XH_n+nH_{n-1}\) et ainsi \(H_n’=nH_{n-1}\).
Résultats immédiats :
\( H_0(x) = 1
H_1(x) = x
H_2(x) = x^2 – 1
H_3(x) = x^3 – 3x
H_4(x) = x^4 – 6x^2 + 3\)
Étude du terme dominant des polynômes d’Hermite
On peut montrer par récurrence que le terme dominant des polynômes d’Hermite est \(X^n\). Pour cela, on utilise une récurrence double avec l’hypothèse de récurrence \(P_n\): « le coefficient dominant est \(X^n\) »
Initialisation : \( H_0=1=X^0\) et\(H_1=X=X^1\)
Hérédité : Soit \(n\) un entier naturel tel que \(P_n\) est vraie. On utilise la relation \(H_{n+1} =XH_n-nH_{n-1}’\).
\(XH_n\) a pour coefficient dominant \(X^{n+1}\) et \(-nH_{n-1}’\) a pour coefficient dominant \(-n(n-1)X^{n-2}\) d’où le coefficient de \(H_{n+1}\) est égal à \(X^{n+1}\).
Orthogonalité de la famille des polynômes d’Hermite
Polynômes d’Hermite et orthogonalité :
\( \forall n \in \mathbb{N}, ({H_0, H_1, … , H_n)}\) est une famille orthogonale (mais pas orthonormée) de \(\mathbb{R}_n[X]\). Par conséquent, elle est libre et comme elle est de dimension \(n + 1\), il s’agit d’une base de \(\mathbb{R}_n[X]\).
Montrons que les polynômes d’Hermite sont orthogonaux pour le produit scalaire \(<P,Q>=\displaystyle \int_{-\infty}^{+
\infty} P(t)Q(t)h_n(t) \, \mathrm{d}t\)
Soient \((i ; j) \in \mathbb{N}^2\) avec \( i < j\).
\( < H_i; H_j > \ = \displaystyle \int_{-\infty}^{+\infty} H_i(t)H_j(t)\phi(t) \, \mathrm{d}t \)
\(< H_i; H_j > \ = \displaystyle \int_{-\infty}^{+\infty} H_i(t) (-1)^j\phi^{(j)}(t)\, \mathrm{d}t \)
En posant \( u(t) = H_i(t) \) et \(v'(t) = (-1)^j\phi^{(j)}(t)\), on a \(u'(t) = iH_{i – 1}(t)\) et \(v(t) = (-1)^j\phi^{(j – 1)}(t)\).
\( < H_i; H_j > \ = [H_i(t)(-1)^j\phi^{(j – 1)}(t)]_{-\infty}^{+\infty} – \displaystyle \int_{-\infty}^{+\infty}iH_{i – 1}(t)(-1)^j\phi^{(j)}(t)\, \mathrm{d}t \)
\( < H_i; H_j > \ = [-\phi(t)H_{j – 1}H_i(t)]_{-\infty}^{+\infty} + i\displaystyle \int_{-\infty}^{+\infty}H_{i – 1}(t)H_{j – 1}(t)\phi(t)\, \mathrm{d}t \)
Or, \( < H_i; H_j > \ = [-\phi(t)H_{j – 1}H_i(t)]_{-\infty}^{+\infty} = 0 \)
et \(\displaystyle \int_{-\infty}^{+\infty}H_{i – 1}(t)H_{j – 1}(t)\phi(t)\, \mathrm{d}t = \ < H_{i – 1}; H_{j – 1}>\).
Donc, pour \((i ; j) \in \mathbb{N}^2\) avec \( i < j\),
\( < H_i; H_j > \ = i < H_{i – 1}; H_{j – 1}>\)
\( < H_i; H_j > \ = i (i – 1) < H_{i – 2}; H_{j – 2}>\)
D’où \( < H_i; H_j > \ = i! < H_{0}; H_{j – i}>\) par itérations successives.
On obtient alors :
\( < H_i; H_j > \ = i! \displaystyle \int_{-\infty}^{+\infty}H_{0}(t)H_{j – i}(t)\, \mathrm{d}t\)
\( < H_i; H_j > \ = i! \displaystyle \int_{-\infty}^{+\infty} 1 \times (-1)^{j – i}\phi^{(j – i)}(t)\, \mathrm{d}t\)
\( < H_i; H_j > \ = i! (-1)^{j – i} [\phi^{(j – i – 1)}(t)]_{-\infty}^{+\infty}\)
\( < H_i; H_j > \ = i! (-1)^{j – i} [\frac{1}{(-1)^{(j – i – 1)}}H_{j – i – 1}(t) \phi(t)]_{-\infty}^{+\infty}\)
Soit finalement \( < H_i; H_j > \ = 0\).
Donc, la famille \(({H_0, H_1, … , H_n)}_{n \ge 0}\) est une famille orthogonale de \(\mathbb{R}[X]\).
On pourrait également montrer que \(\forall k \in \mathbb{N}, deg H_k = k\).
Donc, \(\forall n \in \mathbb{N}, ({H_0, H_1, … , H_n)}\) est une famille orthogonale de \(\mathbb{R}_n[X]\), donc libre et c’est une base.
Cette famille n’est en revanche pas orthonormée.
Après calculs, on trouve que \(\|H_0\| = (2\pi)^{\frac{1}{4}}\).
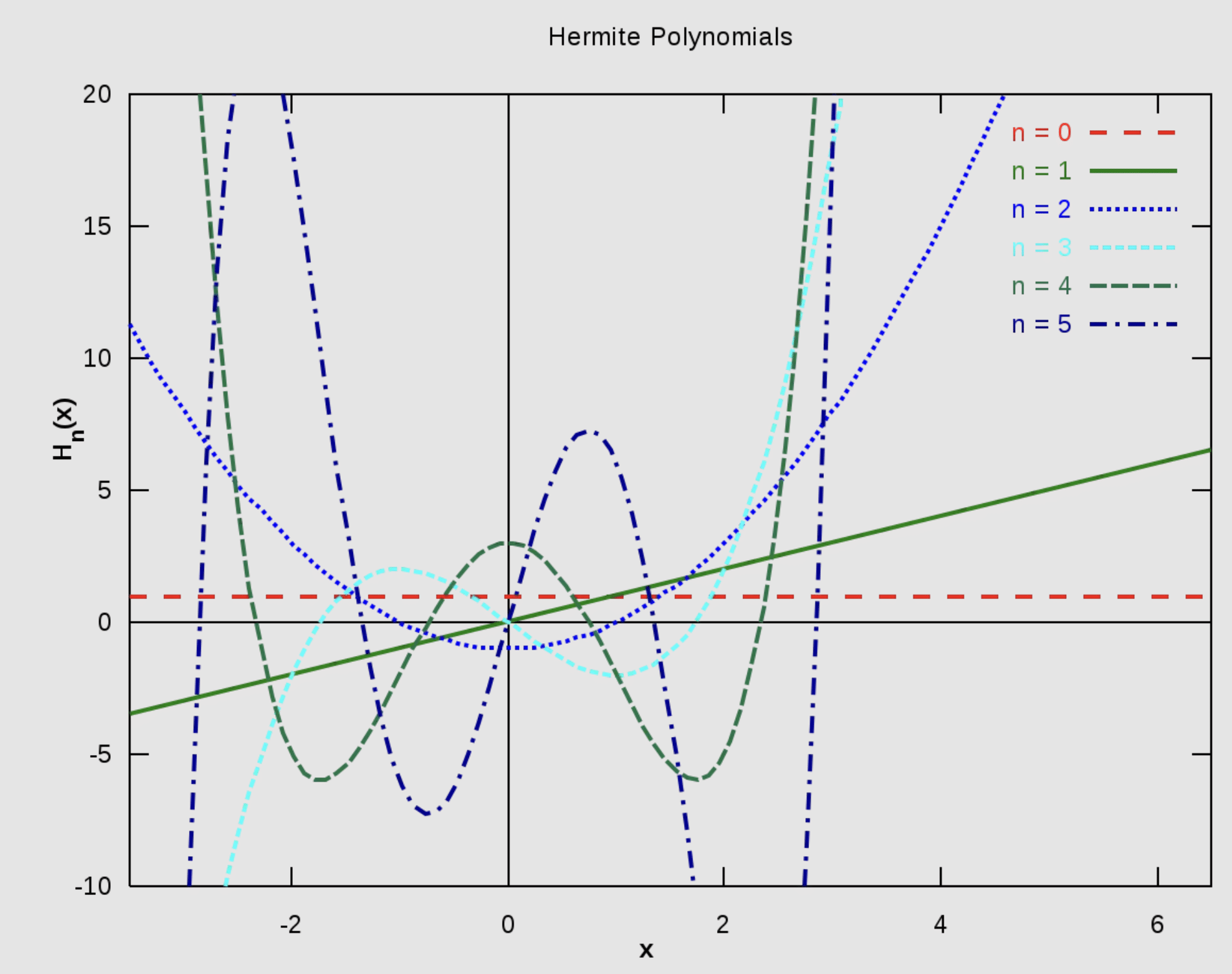
Représentation graphique des polynômes d’Hermite
Le schéma ci-dessous représente graphiquement les premiers polynômes d’Hermite :
Remarque
En tant que famille de polynômes de degrés échelonnés, on peut construire une base d’un espace vectoriel de polynômes à partir des polynômes d’Hermite !
Sujet de concours avec la notion des polynômes d’Hermite
Pour voir toutes nos ressources de mathématiques, tu peux cliquer ici !