En plus de fournir une source inépuisable de problèmes pour les concepteurs d’épreuves, le polynôme interpolateur de Lagrange permet de réviser aussi bien l’analyse que l’algèbre. Regardons cet objet mathématique bien utile pour les concours sous ces deux angles.
1. Principe du polynôme de Lagrange
L’interpolation de Lagrange répond à un problème simple en apparence, comme souvent en mathématiques. À savoir, quelle fonction coïncide avec un nombre fini de points et permet de joindre un nombre \(n\) fini de points. Le polynôme interpolateur de Lagrange fournit non seulement une solution au problème, mais est également l’unique polynôme de rang \(n-1\) à être solution.
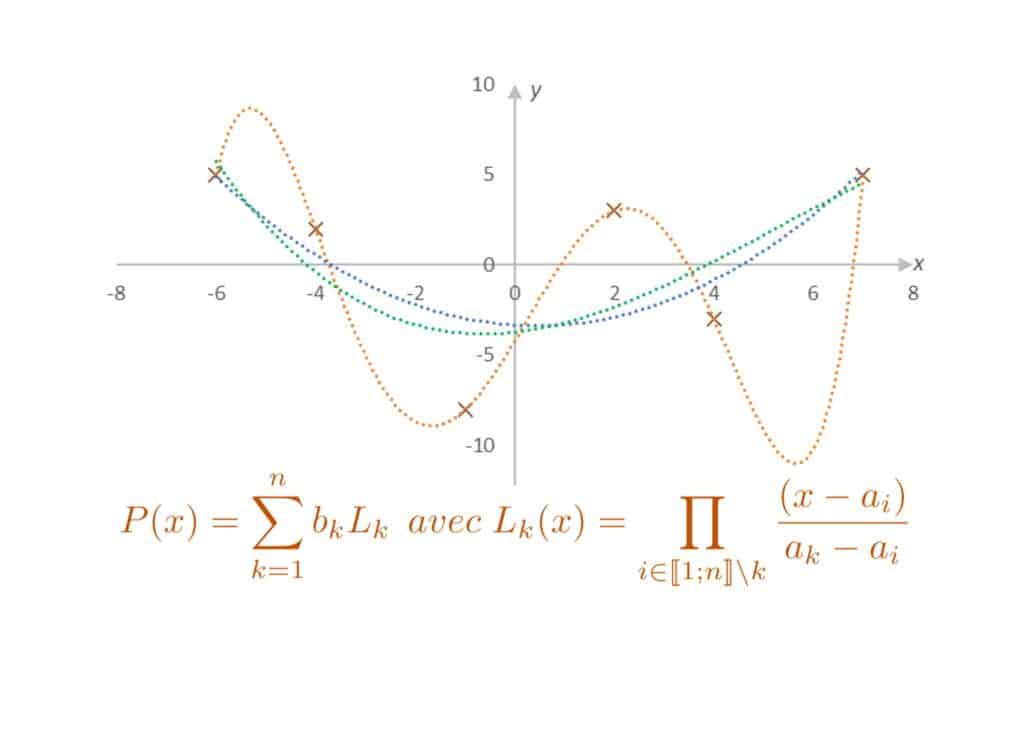
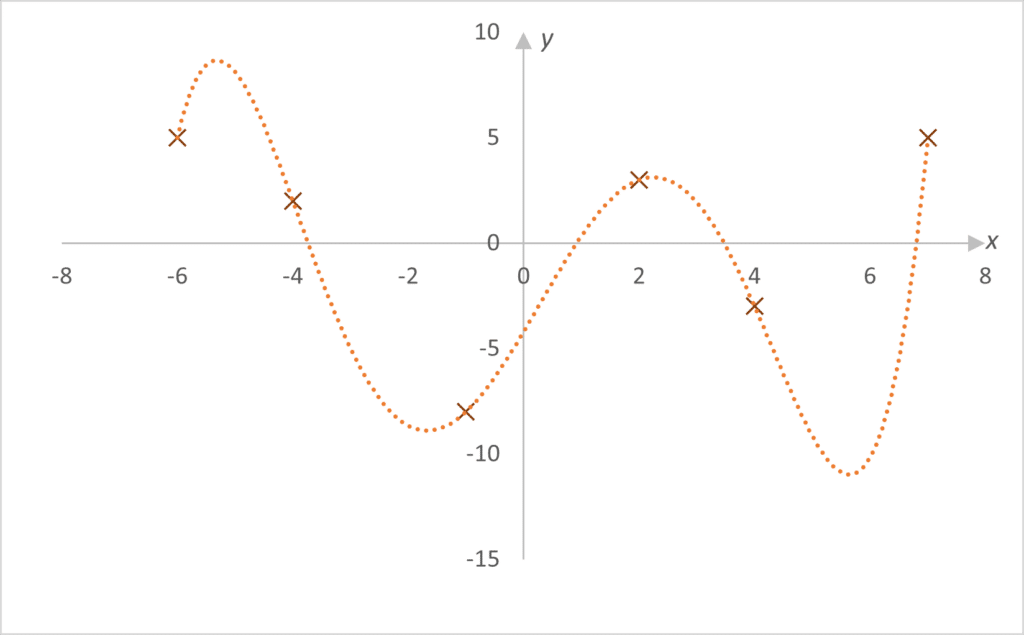
En image, si l’on cherche à interpoler la série \(D\) de points suivants \(D=((-6;5);(-4;2);(-1;-8);(2;3);(4;-3);(7;-5))\), représentée ci-dessous par les croix marron, on trouve le polynôme de degré 5 représenté par le trait en pointillé.
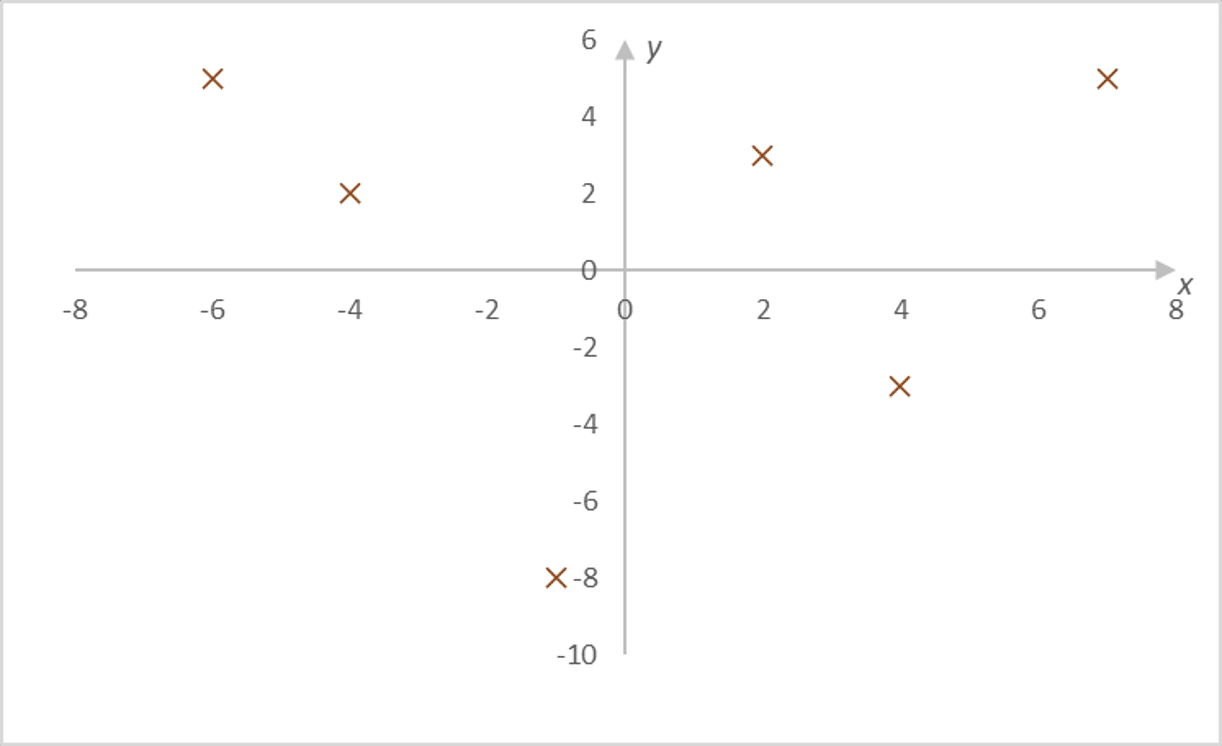
2. Approche par l’analyse des polynômes de Lagrange
Construction du polynôme d’interpolation de Lagrange
Considérons une série de points dans \(R^2\) notée \(D\) avec \(D=((a_i;b_i), i\in [\![1;n]\!]\)).
On cherche d’abord pour tout \(k\in [\![1;n]\!]\) un polynôme \(L_k\in\mathbf{C_{n-1}[X]}\) tel que :
\( L_k(a_i)=\begin{cases} 1 &\text{si}\; k = i\\ 0 &\text{sinon} \end{cases}\).
Remarquons que le polynôme souhaité possède \(n-1\) racines (l’ensemble des \(a_i; i \in [\![1;n]\!] \) excepté \(a_k\)). Pour avoir ces \(n-1\) racines, il suffit que le polynôme soit sous la forme \(\displaystyle \prod_{i \in [\![1;n]\!] \backslash \{k\}} (x-a_i)\).
Enfin, comme on souhaite que \( L_k(a_k)=1\), on divise astucieusement le résultat précédent par \(\displaystyle \prod_{i \in [\![1;n]\!] \backslash \{k\}} (a_k-a_i)\) de sorte que lorsqu’on évaluera \( L_k\) en \( a_k\), on trouvera :
\( L_k(a_k)=\displaystyle \prod_{i \in [\![1;n]\!] \backslash \{k\}} \frac{(a_k-a_i)}{a_k-a_i}=1\).
Et voilà, nous avons trouvé le polynôme \(L_k\) demandé : \( L_k(x)=\displaystyle \prod_{i \in [\![1;n]\!] \backslash \{k\}} \frac{(x-a_i)}{a_k-a_i}\).
Maintenant, pour trouver le polynôme \( P\) de degré au plus \(n-1\) qui passe par les points \(D=((a_i;b_i), i\in [\![1;n]\!]\)), il suffit de prendre \(\displaystyle\sum_{k=1}^nb_kL_k\).
Nous avons alors bien \(\displaystyle \forall i \in [\![1;n]\!],\; \sum_{k=1}^nb_kL_k(a_i) = b_i\).
Unicité du polynôme \( P\) sans utilisation de l’algèbre
Supposons qu’un autre polynôme \( Q\) de degré au plus \(n-1\) vérifie également \(\forall i \in [\![1;n]\!],\; Q(a_i) = b_i\).
Alors, remarquons que le polynôme \( P-Q\) est de degré au plus \(n-1\) et s’annule en \(n\) points distincts (l’ensemble des \(a_i\) avec \( i \in [\![1;n]\!] \), car nous avons \( \forall i \in [\![1;n]\!],\;P(a_i)-Q(a_i) = b_i-b_i=0\).
Donc, \( P-Q=0_{\mathbf{C_{n-1}[X]}}\) et finalement \(P=Q\).
Ainsi, nous avons bien montré l’unicité du polynôme \(P\).
3. Approche par l’algèbre des polynômes de Lagrange
L’algèbre nous aide à démontrer rapidement que le polynôme \( P\) est unique. Pour ce faire, nous allons remarquer que la famille \( L_k, k \in [\![1;n]\!]\) est une base de \(\mathbf{C_{n-1}[X]}\). Puis, nous en déduirons que tout polynôme de \(\mathbf{C_{n-1}[X]}\) admet une décomposition unique dans la base \( (L_k, k \in [\![1;n]\!])\) de la forme \(\displaystyle\sum_{k=1}^nb_kL_k\).
Pour trouver que la famille \( L_k, k \in [\![1;n]\!]\) est une base de \(\mathbf{C_{n-1}[X]}\), nous montrons qu’elle est libre et qu’elle contient \(n\) éléments (puisque \(\mathbf{C_{n-1}[X]}\) est de dimension \(n\)).
Montrons donc la liberté de la famille \( L_k, k \in [\![1;n]\!]\). Soit \((w_k)_{1\leq k \leq n}\) \(n\) réelles et résolvons :
\(\displaystyle\sum_{k=1}^nw_kL_k=0\).
En évaluant pour tout \(i \in [\![1;n]\!]\) la somme en \(a_i\), on obtient :
\(\displaystyle\sum_{k=1}^nw_kL_k(a_i)=0 \Leftrightarrow w_iL_i(x_i)=0 \Leftrightarrow w_i=0 \).
En effet, on rappelle que \( L_k(a_i)=\begin{cases} 1 &\text{si}\; k = i\\ 0 &\text{sinon} \end{cases}\).
Donc, la famille \( L_k, k \in [\![1;n]\!]\) est bien libre. Or, elle contient \(n\) éléments, c’est donc une base de \(\mathbf{C_{n-1}[X]}\).
Ainsi, tout polynôme de \(\mathbf{C_{n-1}[X]}\) admet une décomposition unique dans la base \( (L_k, k \in [\![1;n]\!])\) de la forme \(\displaystyle\sum_{k=1}^nb_kL_k\).
Conclusion
Cette notion, très utile pour réviser ses connaissances en polynômes ou en algèbre, est déjà tombée aux concours sous diverses formes. Ainsi, en 2019, l’EDHEC propose notamment l’étude de cet objet mathématique. Tu trouveras cette notions dans l‘exercice 2 d’ECRICOME 2024, l’exercice 1 de d’EDHEC 2019, ou dans les maths HEC 2017.