L’étude de polynômes particuliers est un exercice qui revient souvent au concours, et ce, pour toutes les épreuves de mathématiques. L’objectif de cet article est d’étudier plus en profondeur les polynômes de Laguerre et de résoudre les questions « classiques » relatives à ces polynômes.
Dans tout l’article, \(n \in \mathbb{N}\) et \(x \in \mathbb{R}\).
Définition
On définit les polynômes de Laguerre par : \(L_n(x)=\frac{e^x}{n!}h_n^{(n)}(x)\) avec \(h_n(x)=x^ne^(-x)\).
Étude des premiers termes et graphe des polynômes
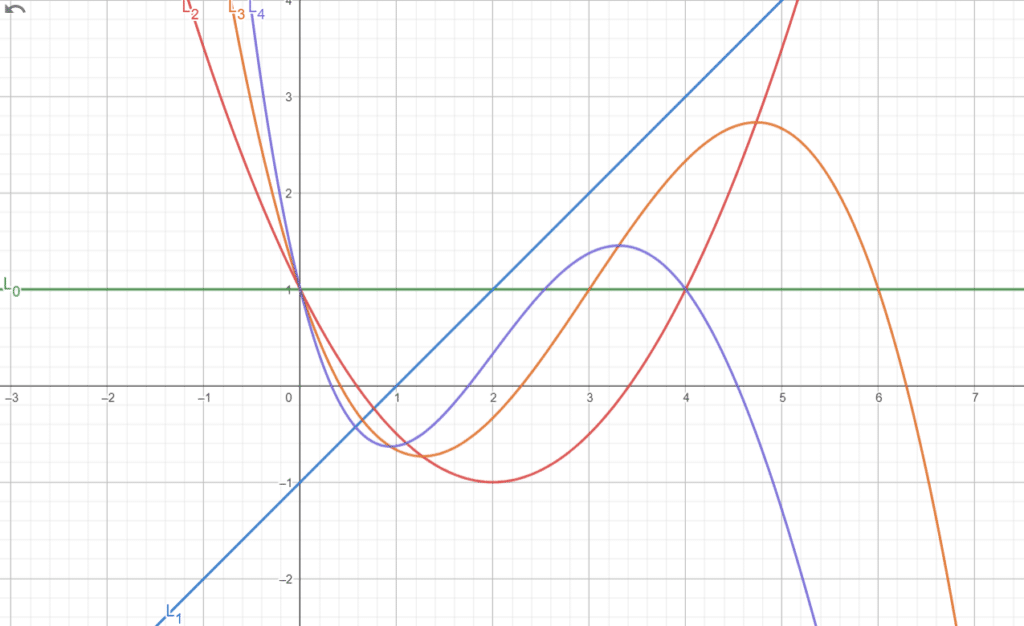
\(L_0(X)=1\)
\(h_1′(x)=e^(X)(1-x)\). On a donc \(L_1(X)=X-1\).
\(h_2′(x)=e^(-x)(2x-x^2)\), \(h_2^(2)(x)=e^(-x)(2-4x+x^2)\) d’où \(L_2(X)=\frac{1}{2}(x^2-4x+2)\).
De même, on trouve, \(L_3(X)=\frac{1}{6}(-x^3+9x^2-18x+6)\).
Pour avoir une idée : voici une représentation des premiers polynômes :
Autre écriture du polynôme
Montrons qu’on peut écrire \(L_n(X)=\displaystyle \sum_{k=0}^{n}\frac{(-1)^k}{k!}{{n}\choose{k}}x^k\).
Pour cela, on utilise la formule de Leibniz.
On a \(h_n^{(n)}(x)=(x^ne^(-x))^{(n)}=\displaystyle \sum_{k=0}^{n}{{n}\choose{k}}(e^(-x))^{(k)}(x^n)^{(n-k)}\).
Une récurrence simple nous permet de montrer que \((x^n)^{(n-k)}=\frac{n!}{k!}x^{k}\).
Ainsi, \(h_n^{(n)}(x)=\displaystyle \sum_{k=0}^{n}{{n}\choose{k}}(e^(-x))^{(k)}(x^n)^{(n-k)}=\displaystyle \sum_{k=0}^{n}{{n}\choose{k}}(-1)^ke^(-x)\frac{n!}{(k)!}x^{k}\)
D’où \(L_n(x)=\frac{e^(x)}{n!}h_n^{(n)}(x)=\frac{e^(x)}{n!}\displaystyle \sum_{k=0}^{n}{{n}\choose{k}}(-1)^ke^(-x)\frac{n!}{(k)!}x^{k}=\displaystyle \sum_{k=0}^{n}\frac{(-1)^k}{k!}{{n}\choose{k}}x^k\).
Étude du coefficient dominant
Cette nouvelle écriture des polynômes de Laguerre nous permet d’identifier très facilement le coefficient dominant de \(L_n\).
En effet, cette écriture montre bien que \(L_n\) est une fonction polynomiale de degré \(n\). On trouve ainsi que son coefficient dominant est égal à \(\frac{(-1)^n}{n!}\).
Première relation de récurrence
Montrons que \(L_{n+1}'(x)=L_n'(x)-L_n(x)\).
Tout d’abord, montrons que \(h_{n+1}'(x)=(n+1)h_n(x)-h_{n+1}(x)\).
On a \(h_{n+1}'(x)=(n+1)x^ne^(-x)-x^(n+1)e^(-x)=(n+1)h_n(x)-h_{n+1}(x)\).
Notons que \(L_n'(x)=\frac{(e^xh_n^{(n)})’}{n!}=\frac{e^xh_n^{(n)}+e^xh_n^{(n+1)}(x)}{n!}=L_n(x)+\frac{e^xh_n^{(n+1)}(x)}{n!}\).
De même, \(L_{n+1}'(x)=L_(n+1)+\frac{e^xh_(n+1)^{(n+2)}(x)}{n!}\)
En dérivant \(n+1\) fois cette égalité : \(h_{n+1}'(x)=(n+1)h_n(x)-h_{n+1}(x)\), on obtient \(h_{n+1}^{(n+2)}(x)=(n+1)h_n^{(n+1)}(x)-h_{n+1}^{(n+1)}(x)\).
En multipliant par \(\frac{e^x}{n!}\), on obtient : \(\frac{e^xh_(n+1)^{(n+2)}(x)}{n!}=\frac{e^xh_n^{(n+1)}(x)}{n!}-L_{n+1}(x)\) d’où \(L_{n+1}'(x)-L_{n+1}(x)=L_n'(x)-L_n(x)-L_{n+1}(x)\). Finalement on trouve bien \(L_{n+1}'(x)=L_n'(x)-L_n(x)\).
Seconde relation de récurrence
Montrons que \((n+1)L_{n+1}(x)=xL_n'(x)+(n+1-x)L_n(x)\).
Tout d’abord, on a \(h_{n+1}(x)=x^{n+1}e^(-x)=xh_n(x)\).
En dérivant cette égalité \(n+1\) fois avec la formule de Leibniz (deux termes sont non nuls, car la dérivée \(n\)-ème de \(x\) est nulle pour n supérieur ou égal à 2), on trouve : \(h_{n+1}^{(n+1)}(x)=xh_n^{(n+1)}(x)+h_n^(n)(x)\).
En multipliant par \(\frac{e^x}{n!}\), on trouve : \((n+1)L_{n+1}(x)=\frac{e^xxh_n^{(n+1)}(x)}{n!}+(n+1)L_n(x)\).
Nous avons déjà montré que : \(L_n'(x)=L_n(x)+\frac{e^xh_n^{(n+1)}(x)}{n!}\).
On trouve donc : \((n+1)L_{n+1}(x)=xL_n'(x)-xL_n(x)+(n+1)L_n(x)\)
Ainsi, on a bien montré que : \((n+1)L_{n+1}(x)=xL_n'(x)+(n+1-x)L_n(x)\).
En plus : équation différentielle de Laguerre
En dérivant la seconde relation de récurrence, on trouve \((n+1)L_{n+1}'(x)=xL_n”(x)+(n+2-x)L_n'(x)-L_n(x)\).
En introduisant la première relation de récurrence, on obtient \(xL_n^(2)(x)-(x-1)L_n'(x)+nL_n(x)=0\).
Ainsi, \(L_n\) est solution de l’équation différentielle : \(xy’^(2)+(1-x)y’+ny=0\). On appelle cette équation différentielle « l’équation de Laguerre ».
Orthogonalité
Les polynômes de Laguerre forment une famille orthogonale pour le produit scalaire \(<f,g>=\int_{0}^{+\infty} f(t)g(t)e^(-t) \, \mathrm{d}t\).
Pour montrer cela, nous allons utiliser la relation de l’équation différentielle de Laguerre, à savoir : \(xL_n’^(2)(x)-(x-1)L_n'(x)+nL_n(x)=0\). On pose l’application \(T\) telle que pour tout polynôme \(P\), \(T(P)(x)=xP^(2)(x)-(x-1)P'(x)\). On note ainsi que \(T(L_n)=-nL_n\).
Une étude intermédiaire nous permet de montrer que \(T\) est symétrique pour le produit scalaire étudié. Ainsi pour tout polynôme \(P\) et\(Q\), on trouve \(<T(P),Q>=<P,T(Q)>\).
Soit \(i \ne j\).
On a \(<T(L_i),L_j>=<-iL_i,L_j>=-i<L_i,L_j>\)
Or, en utilisant la symétrie de \(T\), on a également \(<T(L_i),L_j>=<L_i,T(L_j)>=-j<L_i,L_j>\).
Finalement, on a \((i-j)<L_i,L_j>=0\) et \(i \ne j\) donc \(<L_i,L_j>=0\)
La famille des polynômes de Laguerre est donc une famille orthogonale pour ce produit scalaire.
Remarque
Soit \(N \in \mathbb{N}\). On note \(E_N\) le sous-espace vectoriel formé des applications polynomiales de \(\mathbb{R}\) dans \(\mathbb{R}\) de degré inférieur ou égal à \(N\).
Alors, la famille \((L_0,…,L_N)\) est une famille orthogonale et libre de \(E_N\) (polynômes de degré échelonnés). Ainsi, \((L_0,…,L_N)\) est une base de \(E_N\). Les polynômes de Laguerre peuvent donc former une base d’un espace vectoriel.
Pour aller plus loin
Tu peux t’entrainer sur les polynômes de Laguerre en faisant le sujet de mathématiques ECS de l’EMLyon de 2011 (sujet, corrigé)
N’hésite pas à consulter toutes nos ressources mathématiques.