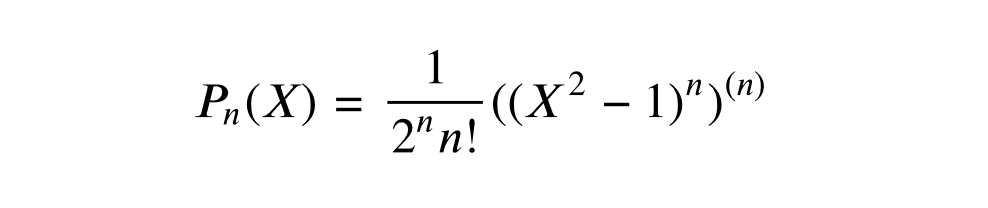Les polynômes de Legendre sont un pilier fondamental dans le domaine de l’analyse mathématique, en particulier dans les problèmes liés aux équations différentielles et à l’approximation de fonctions. Cet article se concentre sur la présentation de ces polynômes, leurs propriétés essentielles et leur application dans des contextes mathématiquement riches, le tout adapté aux étudiants désireux d’approfondir leurs révisions. Ainsi, bien que cette notion soit hors programme, une compréhension approfondie de cette dernière te permettra de mieux te préparer aux épreuves parisiennes et aux oraux de mathématiques !
Définition et origine
Les polynômes de Legendre se définissent comme la solution de l’équation différentielle de Legendre :
\[ \frac{d}{dx}\left[ (1-x^2) \frac{dP_n(x)}{dx} \right] + n(n+1)P_n(x) = 0 \]
Où \(n\) est un entier non négatif et \(P_n(x)\) représente le \( n\text{-ème} \) polynôme de Legendre.
Ces polynômes sont ici définis sur l’intervalle \([-1, 1]\) et jouent un rôle crucial dans les problèmes d’approximation et dans le développement en série de fonctions.
La formule de Rodrigues
Nous pouvons aussi définir les polynômes de Legendre de la façon suivante, appelée formule de Rodrigues :
\[ \displaystyle P_n(X) = \frac{1}{2^nn!}((X^2-1)^n)^{(n)}\]
Définition sous forme de sommes
En plus de la formule de Rodrigues, les polynômes de Legendre peuvent également être exprimés sous forme de sommes. Ce qui offre une perspective différente sur leur structure. Ces sommes sont particulièrement utiles pour les calculs explicites et pour l’analyse combinatoire.
Voici les deux définitions sous forme de sommes :
La première définition exprime le n-ième polynôme de Legendre, \( P_n(x) \), comme une somme alternée :
\[ \displaystyle P_n(x) = \frac{1}{2^n} \sum_{k=0}^{\lfloor \frac{n}{2} \rfloor} (-1)^k {{n}\choose{k}} {{2n-2k}\choose{n}} x^{n-2k}. \]
Cette représentation est particulièrement utile pour calculer des valeurs spécifiques des polynômes de Legendre, comme \( P_{2n}(0) \), qui découle directement de la série lorsque \( x = 0 \) : \( \displaystyle P_{2n}(0) = \frac{1}{2^{2n}} (-1)^n {{2n}\choose{n}}. \)
La seconde définition utilise une approche similaire, décomposant \( P_n(x) \) en une somme de termes binomiaux :
\[ P_n(x) = \frac{1}{2^n} \sum_{k=0}^{n} {{n}\choose{k}}^2 (x-1)^{n-k} (x+1)^k. \]
Cette forme est avantageuse lorsqu’il s’agit de développer les polynômes de Legendre en série autour de points tels que \( x = 1 \) ou \( x = -1 \).
Ces deux sommes permettent finalement de comprendre la composition des polynômes de Legendre et d’explorer leurs propriétés algébriques plus en détail.
Expression des premiers polynômes de Legendre
Pour une meilleure intuition des polynômes de Legendre, il est utile d’examiner les premières instances. Les polynômes de Legendre sont construits de manière à former une base orthogonale. Le terme le plus simple, \(L_0(x)\), est simplement la constante 1. Cela sert de fondement sur lequel les termes suivants sont construits, en augmentant le degré tout en conservant l’orthogonalité.
Voici les premiers polynômes de Legendre :
\(L_0(x) = 1\)
\(L_1(x) = x\)
\(L_2(x) = \frac{1}{2}(3x^2 – 1)\)
\(L_3(x) = \frac{1}{2}(5x^3 – 3x)\)
\(L_4(x) = \frac{1}{8}(35x^4 – 30x^2 + 3)\)
\(L_5(x) = \frac{1}{8}(63x^5 – 70x^3 + 15x)\)
Orthogonalité et orthonormalité des polynômes de Legendre
L’orthogonalité des polynômes de Legendre est une de leurs caractéristiques les plus notables et est cruciale pour leur utilisation en analyse mathématique. Elle est définie par le produit scalaire dans l’espace des fonctions continues sur l’intervalle \([-1, 1]\). Pour deux fonctions \(P\) et \(Q\), le produit scalaire est donné par : \( \displaystyle \langle P, Q \rangle = \int_{-1}^{1} P(t)Q(t)dt. \)
Deux polynômes de Legendre de degrés différents, \(L_m\) et \(L_n\), sont orthogonaux par rapport à ce produit scalaire. C’est-à-dire que leur produit scalaire est nul si \(m \neq n\).
Cependant, les polynômes de Legendre ne sont pas orthonormaux, car le produit scalaire d’un polynôme de Legendre avec lui-même n’est pas égal à 1, mais à \( \displaystyle \frac{2}{2n+1}\).
La relation est donc : \( \displaystyle \langle L_n, L_n \rangle = \frac{2}{2n+1}. \)
Pour obtenir des polynômes orthonormaux, il faudrait diviser chaque polynôme de Legendre \(L_n(x)\) par la racine carrée de \( \displaystyle \frac{2}{2n+1}\), donnant lieu à une nouvelle série de polynômes, les polynômes de Legendre orthonormaux.
Propriétés fondamentales des polynômes de Legendre
Les polynômes de Legendre possèdent plusieurs propriétés remarquables qui en font un outil précieux pour les mathématiciens.
Degré des polynômes de Legendre
Nous savons que \( \displaystyle L_n(X) = \frac{1}{2^nn!}((X^2-1)^n)^{(n)}.\) Donc, le polynôme \(L_n,\) étant la dérivée \( n-\text{ème} \) d’un polynôme de degré \(2n,\) est donc de degré \(n.\)
Coefficient dominant des polynômes de Legendre
Le coefficient dominant d’un polynôme est le coefficient du terme de plus haut degré. Pour \(P_n(x)\), le coefficient dominant est donné par \( \displaystyle \frac{(2n)!}{2^n(n!)^2}\).
Base de l’espace vectoriel des polynômes
La famille des polynômes de Legendre \( (P_n)_{0 \leq n \leq N} \) forme une base de l’espace vectoriel des polynômes de degré inférieur ou égal à \(N\), noté \( \mathbb{R}_N[X] \). Cela signifie que tout polynôme de degré \(N\) ou inférieur peut être exprimé comme une unique combinaison linéaire des polynômes de Legendre jusqu’à \(P_N\).
Parité des polynômes de Legendre
La parité d’un polynôme est une propriété qui indique la symétrie de sa représentation graphique par rapport à l’origine. Les polynômes de Legendre ont la même parité que leur degré \(n\). Si \(n\) est pair, \(P_n(x)\) est pair, et si \(n\) est impair, \(P_n(x)\) est impair.
Ce qui se traduit mathématiquement par :
\[ P_n(-x) = (-1)^n P_n(x). \]
Cette propriété de parité est particulièrement utile pour intégrer des polynômes de Legendre sur des intervalles symétriques.
Norme des polynômes de Legendre
La norme au carré de \(P_n\), notée \( \|P_n\|^2 \), est égale à \(\frac{2}{2n+1}\). Cela confirme que bien qu’ils ne soient pas orthonormaux, les polynômes de Legendre étant orthogonaux peuvent être normalisés facilement en les divisant par leur norme.
Formule de récurrence des polynômes de Legendre
Les polynômes de Legendre obéissent à une relation de récurrence qui facilite leur calcul et que tu pourrais rencontrer dans un sujet de concours :
\[(n+1)P_{n+1}(x) = (2n+1)xP_n(x) – nP_{n-1}(x).\]
Conclusion
En résumé, les polynômes de Legendre constituent un sujet d’une grande richesse mathématique. Leur étude approfondie nous a permis de comprendre leur rôle central en tant que solutions d’une équation différentielle classique, de découvrir leur expression sous différentes formes et de saisir l’importance de leurs propriétés d’orthogonalité et de parité. La maîtrise des polynômes de Legendre ouvre donc la voie à une meilleure préparation pour les épreuves écrites et orales, soulignant la valeur d’intégrer ces concepts avancés dans tes révisions !
Pour t’entraîner à travailler sur des polynômes particuliers, tu peux réaliser les sujets suivants :
- Maths I 2017 (mathématiques approfondies)
- Maths EML 2016 (mathématiques approfondies)
Tu peux retrouver ici toutes nos autres ressources mathématiques !