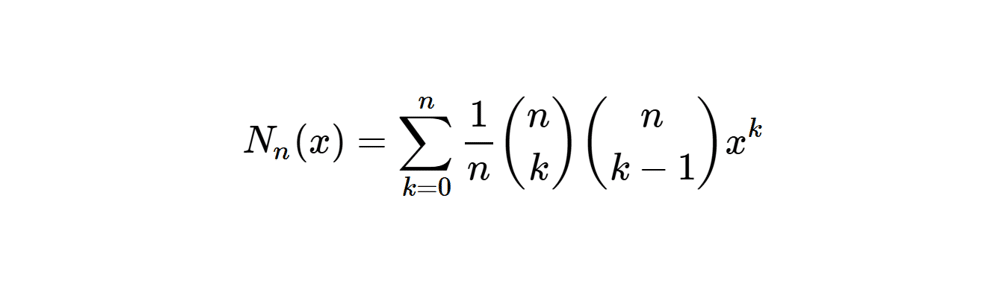Dans cet article, il sera question de la suite de polynômes de Narayana (du nom du mathématicien Tadepalli Narayana) ainsi que des nombres de Narayana qui en découlent. Ces polynômes et ces nombres ont des propriétés intéressantes, notamment en dénombrement, que l’on peut étudier avec les outils du programme d’ECG. Ils ne sont encore jamais tombés aux écrits et peuvent pourtant faire l’objet d’un sujet intéressant.
Introduction
Nous étudierons, dans une première partie, la suite de polynômes de Narayana ainsi que ses propriétés, puis les nombres dits de Narayana qui découlent de cette famille de polynômes et qui ont une portée assez puissante en dénombrement.
Tu verras que les nombres de Narayana sont extrêmement liés aux nombres de Catalan.
Polynômes de Narayana
Définition
On appelle polynôme de Narayana d’ordre n, le polynôme défini par :
\(\forall x \in\mathbb{N}, N_n(x) = \displaystyle \sum_{k=0}^{n}N(n,k)x^k\), où \(N(n,k)\) est définie par :
\(\forall k \in [\![1,n]\!], N(n,k) = \frac{1}{n}{{n}\choose{k}}{{n}\choose{k-1}}\)
Par convention, on a \(N(0,k) = \begin{cases} 1
&\text{si} \; k=0 \\ 0 &\text{sinon}
\end{cases}\)
Attention donc à la gestion des indices pour bien distinguer \(N_n(x)\) de \(N(n,k)\).
Premiers exemples
On peut donc déterminer les premiers polynômes de Narayana. D’après la définition précédente, on obtient alors :
\(N_0(x) = 1\)
\(N_1(x) = x\)
\(N_2(x) = x^2+x\)
\(N_3(x) = x^3+3x^2+x\)
\(N_4(x) = x^4+6x^3+6x^2+x\)
Passons alors aux propriétés de ces polynômes. Tu peux dès à présent essayer de conjecturer certaines des propriétés des polynômes de Narayana en te basant sur ces premiers exemples.
Propriétés
Degré et coefficient dominant
D’après les premiers exemples précédents, on peut conjecturer la propriété suivante :
\(\forall n \in \mathbb{N}, deg(N_n) = n\) et \(N_n\) est de coefficient dominant 1.
Le degré de\(N_n\) est immédiat, d’après l’écriture du polynôme sous forme de somme. En effet, en retournant à la définition du polynôme et en s’intéressant au terme de plus haut degré, on remarque que ce dernier vaut \(N(n,n)\). Calculons alors la valeur de \(N(n,n)\) pour démontrer que cet élément est égal à 1 :
\(N(n,n) = \frac{1}{n}{{n}\choose{n}}{{n}\choose{n-1}} = \frac{1}{n}{{n}\choose{n-1}} =\frac{1}{n} n = 1\)
Relation avec le nombre de Catalan
On a la propriété suivante :
\(\forall n \in \mathbb{N}, N_n(1)= C_n\), où \(C_n\) est le nombre de Catalan d’ordre n. Pour rappel, \(C_n\) est définie par :
\(\forall n \in \mathbb{N}, C_n = \frac{1}{n+1}{{2n}\choose{n}}\)
La démonstration de cette propriété est assez technique. En retournant à la définition du polynôme, on se rend compte que l’on doit sommer le produit de deux coefficients binomiaux dépendants de notre indice de sommation \(k\).
Les nombres de Catalan ont des propriétés très intéressantes, notamment en dénombrement.
Relation avec le nombre de Schröder
On a la propriété suivante :
\(\forall n \in \mathbb{N}, N_n(2)= r_n\), où \(r_n\) est le n-ième nombre de Schröder.
Puisque, les premiers nombres de Schröder sont 1, 2, 6, 22 et 90, tu pourras vérifier que cette propriété fonctionne bien pour les premiers polynômes de Narayana. Là encore, la démonstration de cette propriété est complètement hors programme, car elle nécessite la gestion des deux coefficients binomiaux dans la somme et en plus du \(2^k\) qui est en produit des deux coefficients binomiaux.
Le nombre de Schröder d’ordre \(n\) représente les chemins dans une grille de taille \(n*n\) reliant les points \((0,0)\) et \((n,n)\) en utilisant seulement des pas unités de direction nord, nord-est ou est, et qui ne dépassent pas la diagonale sud-ouest/nord-est.
Voici une représentation graphique dans le cas \( n=2 \) qui permet de bien comprendre la notion :

On comprend donc que les polynômes de Narayana ont des propriétés intéressantes en dénombrement, notamment issues de leurs liens avec les nombres de Catalan et les nombres de Schröder.
Autres écritures
Il existe deux autres écritures des polynômes de Narayana. La première écriture par récurrence donne la formule suivante :
\(\forall n \ge 3, N_n(x) = (1+x)N_{n-1}(x) + x\displaystyle \sum_{k=1}^{n-2}N_k(x)N_{n-k-1}(x)\)
On peut également définir une autre formule explicite de \(N-n\) sous la forme d’une somme en se rapprochant de la première définition de ces polynômes. On a alors :
\(\forall n \in \mathbb{N}, N_n(x) = \displaystyle \sum_{k=0}^{n} \frac{1}{n+1}{{n-1}\choose{k}}{{2n-k}\choose{n}}(x-1)^k\)
Toutefois, ces deux formules restent assez complexes à manipuler et il est peu probable que ces dernières soient étudiées en profondeur dans un sujet d’écrit (sinon un sujet extrêmement exigeant de Maths 1).
Nombres de Narayana
Définition
Il y a un lien direct entre les polynômes de Narayana et les nombres de Narayana. En effet, les nombres de Narayana ne sont autres que les \(N(n,k)\) que l’on retrouve dans la définition des polynômes de Narayana. Pour rappel, les nombres de Narayana sont donc définis par :
\(\forall n \in \mathbb{N^{*}}, \forall k \in [\![1,n]\!], N(n,k) =\frac{1}{n}{{n}\choose{k}}{{n}\choose{k-1}}\)
À l’aide de la formule du capitaine (également appelée « formule sans nom »), les nombres de Narayana se réécrivent de la manière suivante :
\(\forall n \in \mathbb{N^{*}}, \forall k \in [\![1,n]\!], N(n,k) =\frac{1}{k}{{n-1}\choose{k-1}}{{n}\choose{k-1}}\)
La démonstration de cette égalité est assez immédiate et se trouve en appliquant la formule du capitaine au premier coefficient binomial.
On dispose donc d’une table avec les premiers nombres de Narayana en fonction des différentes valeurs de \(n\) et de \(k\) :
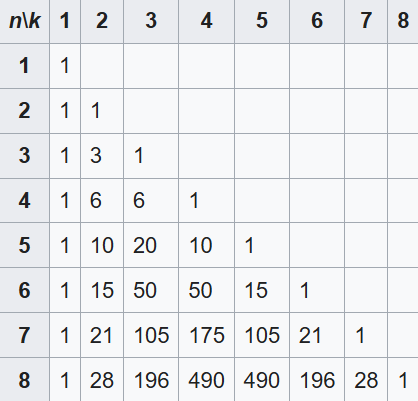
Pour rappel, on a nécessairement \( k \le n \), ce qui explique le triangle formé par les valeurs du tableau.
Propriétés
Lien avec les nombres de Catalan
D’après le lien entre les polynômes et les nombres de Catalan, on comprend directement que pour obtenir \(C_n\) à partir de ce tableau, il suffit de sommer toutes les cases de la \(n\)-ième ligne.
En effet, d’après les propriétés du polynôme de Narayana, ce dernier est égal à \(C_n\) pour \((x=1)\), ce qui revient par définition du polynôme à sommer tous les nombres de Narayana pour une valeur de \(n\) donnée.
Ainsi, les nombres de Narayana ont un lien très précis avec les nombres de Catalan !
Conclusion
Les polynômes et les nombres de Narayana possèdent un grand nombre de propriétés intéressantes que l’on peut étudier avec les outils du programme d’ECG. Puisqu’ils sont liés aux nombres de Catalan et que ces derniers sont déjà tombés au concours, voici ici le lien vers le sujet.
Tu peux retrouver ici le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder ici à toutes nos autres ressources mathématiques !