Résolu au XVIIIe siècle par le mathématicien suisse Leonhard Euler, le problème des sept ponts de Königsberg est un des problèmes fondateurs de la théorie des graphes, une notion clé à maîtriser pour les étudiants de mathématiques appliquées. Cet article te permettra enfin de comprendre d’où vient cette fameuse théorie.
Leonhard Euler
Leonhard Euler (1707-1783) est un mathématicien et physicien suisse du XVIIIe siècle, qui passa le plus clair de son temps en Allemagne et dans l’empire russe. D’où ses fameux travaux sur la ville de Königsberg.
Euler est un nom qu’il est inconcevable de ne pas croiser en prépa tant ses contributions en mathématiques sont nombreuses, couvrant des domaines aussi variés que le calcul infinitésimal (calcul différentiel et intégral), les nombres complexes (les fameuses formules d’Euler), ou encore la théorie des graphes.
Si tu n’es pas encore très à l’aise avec ce dernier concept, je te conseille d’abord de lire ceci. Cela te permettra de maîtriser les définitions, les mots de vocabulaire et les formules de base de la théorie des graphes, éléments essentiels pour bien comprendre cet article.
La ville de Königsberg et ses ponts
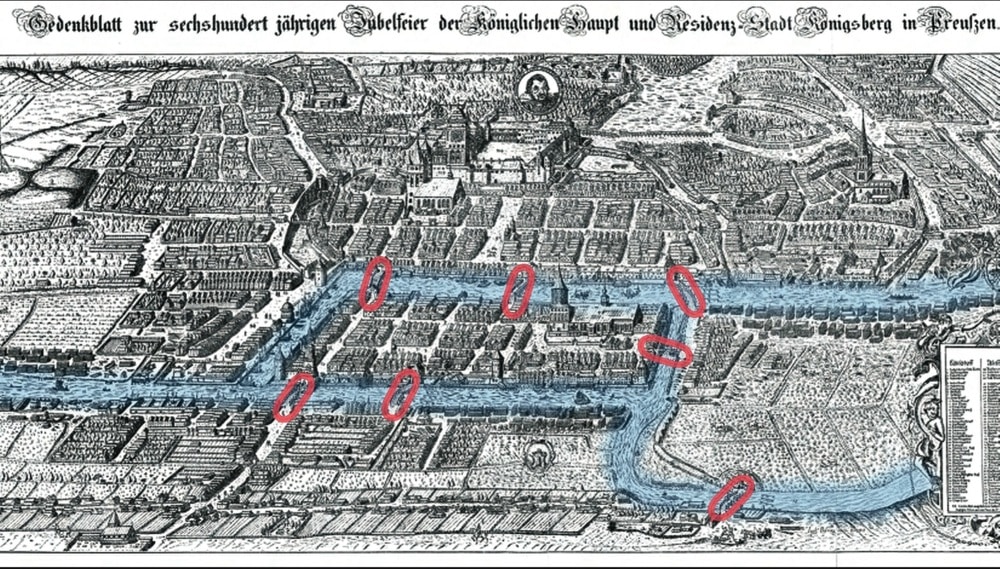
Königsberg, ville située en Russie et aujourd’hui connue sous le nom de Kaliningrad, était traversée par le fleuve Pregel. Celui-ci divisait la ville en plusieurs parties (deux zones terrestres et deux îles) reliées entre elles par sept ponts.
Cette configuration géographique avait ainsi suscité l’interrogation des habitants de la ville, sans soupçonner que cette question, a priori anodine, mènerait à un célèbre problème mathématique : Est-il possible de concevoir une promenade permettant de traverser chaque pont une seule et unique fois, tout en revenant au point de départ ?
Résolution du problème
Aussi décevant que cela puisse paraître, malheureusement… une telle promenade n’existe pas ! S’il est assez intuitif d’en arriver à cette conclusion, c’est Leonhard Euler qui le prouva mathématiquement, même si la démonstration formelle du problème des sept ponts de Königsberg ne fut publiée qu’à la fin du XIXe siècle par le mathématicien Carl Hierholzer, qui confirma que les conditions énoncées par Euler pour résoudre ce casse-tête étaient bel et bien suffisantes.
Alors qu’en est-il de cette résolution ?
Euler a rapidement compris que la clé pour résoudre le problème résidait dans une simplification appropriée du problème. Il a ainsi pris la décision de représenter la ville de Königsberg sous la forme d’un graphe, avec un ensemble de sommets (les quatre zones de la ville) et d’arêtes reliant ces sommets (les sept ponts).
Le schéma ci-dessous illustre cette simplification :

Après simplification, on se retrouve avec un graphe connexe non orienté d’ordre 4 (car il possède bien quatre sommets). Il est également dit simple, car deux sommets distincts sont joints par au plus une arête et il est sans boucle.
Le problème devient alors celui de savoir si ce graphe est un graphe eulérien. Autrement dit, Euler se demande s’il est possible de trouver un cycle eulérien propre à ce graphe. Pour rappel, cela signifie qu’il cherche à savoir si ce graphe possède une chaîne eulérienne fermée, soit une chaîne simple (chaque arête apparaît une seule et unique fois, par exemple A-B-C-D) et fermée (le premier et le dernier sommet de la chaîne sont égaux, par exemple A-B-C-D-A), composée de toutes les arêtes du graphe. En bref, ce cycle eulérien est la clé de notre problème, car il permet de trouver un chemin qui emprunte chaque arête exactement une fois.
Euler a dès lors formulé une règle simple pour déterminer si un graphe contient ou non un cycle eulérien (ce qu’on appelle aujourd’hui le fameux théorème d’Euler) :
- Le graphe doit être connexe et non orienté : il doit être possible d’aller d’un sommet à un autre en suivant les arêtes du graphe (ce qui est bien le cas pour Königsberg).
- Tous les sommets du graphe doivent être de degré pair.
Cela s’explique simplement
Pour parcourir chaque arête une seule fois et revenir à son point de départ, il faut que chaque sommet ait un nombre égal d’entrées et de sorties (d’où le degré pair). Mais si un sommet possède un degré impair, il y aura forcément un déséquilibre. On pourra entrer dans cette zone plus de fois qu’on pourra en sortir.
Or, Euler a rapidement remarqué que chaque sommet du graphe modélisé de la ville de Königsberg avait un degré impair :
- Le sommet A est de degré 5.
- Le sommet B est de degré 3.
- Le sommet C est de degré 3.
- Le sommet D est de degré 3.
Selon le théorème d’Euler, il n’existe aucun cycle eulérien propre à ce graphe. Dit autrement : il n’existe aucune promenade qui permettrait de traverser chaque pont une seule et unique fois, tout en revenant au point de départ.
Si elle n’est pas utile ici, il existe une autre propriété intéressante à connaître concernant le théorème d’Euler
Une chaîne eulérienne non fermée se distingue du cycle eulérien, en ce qu’elle constitue aussi une chaîne simple composée de toutes les arêtes du graphe, mais sans nécessairement revenir au point de départ. Selon le théorème d’Euler, un graphe connexe et non orienté possède une telle chaîne si et seulement si le nombre de sommets du graphe de degré impair est exactement égal à 2. Les deux sommets de degré impair seront par ailleurs les extrémités de cette chaîne.
Conclusion
Bien que le problème des sept ponts de Königsberg ne soit jamais tombé au concours, il reste une bonne application de la théorie des graphes qu’il ne serait pas étonnant de voir arriver dans les années à venir dans les annales parisiennes. Mais désormais, tu as toutes les informations nécessaires pour pouvoir attaquer sereinement une telle éventualité.
Tu peux retrouver le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder à toutes nos autres ressources mathématiques !













