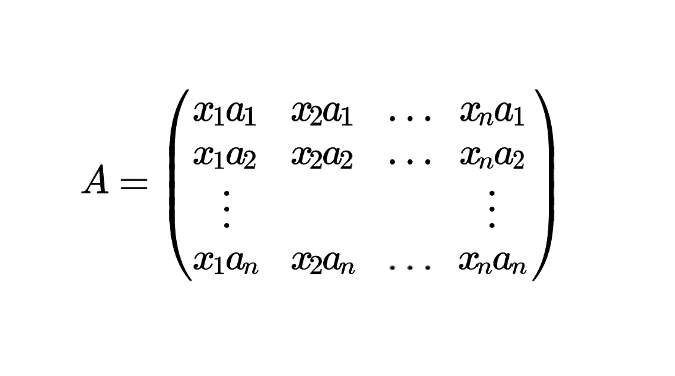L’objectif de cet article est de te donner toutes les astuces relatives aux matrices de rang inférieur ou égal à un. Ces astuces et propriétés peuvent te servir notamment en colles, mais aussi lors des épreuves écrites. C’est souvent les premières questions d’un exercice, il est donc important de savoir les traiter rapidement !
Cet article s’adresse aussi bien aux mathématiques appliquées qu’aux mathématiques approfondies et ECT.
Dans tout l’article, on pose \(n \in \mathbb{N}\).
Les matrices de rang 0
Il n’existe qu’une seule matrice de rang \(0\) dans \(\mathbb{M}n(\mathbb{R})\) et c’est la matrice nulle, la matrice dont tous les coefficients sont nuls.
Propriétés de la matrice nulle \(0_{n,n}\)
Son rang est donc nul.
Elle admet une unique valeur propre \(0\).
Son polynôme caractéristique est \(X^n\). Pour en savoir plus sur les polynômes caractéristiques, tu peux lire cet article.
Sa trace est nulle.
Les matrices de rang 1
Une matrice de rang \(1\) est une matrice dont toutes les colonnes sont multiples.
Par exemple, \(A=\begin{pmatrix} 1 & 2 & 3 \\ 1 & 2 & 3 \\ 1 & 2 & 3 \end{pmatrix}\) est une matrice de rang \(1\).
Propriétés des matrices de rang 1
Une matrice \(A\) est de rang 1 si et seulement s’il existe deux matrices colonnes non nulles \(U\) et \(V\) telles que \(A=U^tV\).
Démonstration
Soit \(A\) une matrice de rang 1, il existe \((a_1,…,a_n)\) et \((x_1,…,x_n)\) des réels non tous nuls tels que \(A=\begin{pmatrix} x_1 a_1 & x_2 a_1 & \ldots & x_n a_1 \\ x_1 a_2 & x_2 a_2 & \ldots & x_n a_2 \\ \vdots & & & \vdots \\ x_1 a_n & x_2 a_n & \ldots & x_n a_n \end{pmatrix} \). On peut donc écrire \(A=U^tV\) avec \(U=\begin{pmatrix} a_1 \\ a_2 \\ \ldots \\ a_n \end{pmatrix}\) et \(V=\begin{pmatrix} x_1 \\ x_2 \\ \ldots \\ x_n \end{pmatrix}\).
La réciproque est immédiate : on pose \((a_1,…,a_n)\) et \((x_1,…,x_n)\) des réels non tous nuls, \(U=\begin{pmatrix} a_1 \\ a_2 \\ \ldots \\ a_n \end{pmatrix}\) et \(V=\begin{pmatrix} x_1 \\ x_2 \\ \ldots \\ x_n \end{pmatrix}\). Soit \(A=U^tV\), on a \(A\) qui est de rang \(1\).
Soit \(A\) une matrice de rang \(1\), il existe \(\lambda\) tel que \(A^2=\lambda A\).
Démonstration
Soit \(A\) une matrice dont le rang vaut \(1\).
D’après la première propriété, il existe deux matrices colonnes non identiquement nulles \(U\) et \(V\) telles que \(A=U^tV\). D’où, \(A^2=U^tVU^tV=Utr(A)^tV=tr(A)U^tV=tr(A)A\). On a donc bien montré qu’il existe un \(\lambda=tr(A)\) tel que \(A^2=\lambda A\).
On en déduit alors le polynôme caractéristique d’une matrice de rang \(1\) et on obtient : \(X(X-\lambda)\) annule \(A\). Autrement dit, \(A(A-tr(A))=0\).
Diagonalisation d’une matrice de rang 1
Les valeurs propres d’une matrice de rang 1
Savoir qu’une matrice \(A\) de \(\mathbb{M}n(\mathbb{R})\) est de rang \(1\) nous donne par le théorème du rang que \(dim(Ker(A))=n-1\). On a donc que \(0\) est une valeur propre de \(A\) et la dimension du sous-espace propre associé est \(n-1\).
Il est possible que \(A\) ait une autre valeur propre et pour la trouver, on s’intéresse au polynôme caractéristique de \(A\). En effet, on sait que les valeurs propres d’une matrice sont parmi les racines du polynôme annulateur de la matrice. Or, le polynôme annulateur de \(A\) est \(A(A-tr(A))\).
Ainsi, la seule autre valeur propre possible pour \(A\) est sa trace, \(tr(A)\).
Condition nécessaire et suffisante de diagonalisation
Pour qu’une matrice \(A\) soit diagonalisable, il faut que \(tr(A)\) soit non nulle.
On le démontre facilement par l’absurde. Supposons \(A\) une matrice de rang \(1\), dont la trace vaut \(0\) diagonalisable. On a alors que \(A\) a pour seule valeur propre \(0\) et que la dimension du sous-espace propre associé est \(n\).
Ainsi, comme \(A\) est diagonalisable, on a que \(A\) est semblable à la matrice diagonale avec que des \(0\) sur la diagonale, c’est-à-dire la matrice nulle. Or, le rang de deux matrices semblables est le même et \(rg(0_{n,n} \ne rg(A)) \).
Donc, par l’absurde, on a montré que si la trace de \(A\) vaut \(0\), alors \(A\) n’est pas diagonalisable.
À l’inverse, si \(tr(A) \ne 0\). \(A\) a pour valeurs propres \(0\) et \(tr(A)\) donc \(A\) est diagonalisable et \(A\) est semblable à la matrice diagonale, dont tous les éléments de la diagonale sont nuls sauf un qui vaut \(tr(A)\).
Exemple d’étude d’une matrice de rang 1
Posons \(A= \begin{pmatrix} 1 & 2 & 3 \\ 1 & 2 & 3 \\ 1 & 2 & 3 \end{pmatrix} \).
\(A\) peut s’écrire \(U^tV\) avec \(U=\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}\) et \(V=\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \).
\(A^2= \begin{pmatrix} 6 & 12 & 18 \\6 & 12 & 18 \\6 & 12 & 18 \end{pmatrix} = 6A\) et on a bien \(tr(A)=1+2+3=6\).
Le spectre de \(A\) est bien \((0,6)\) donc \(A\) est diagonalisable et semblable à la matrice \(D=\begin{pmatrix} 0 & 0 & 0 \\0 & 0 & 0 \\0 & 0 & 6 \end{pmatrix}\).
Ce que tu dois retenir
Il est important de savoir repérer les matrices de rang \(1\) dans un énoncé et nous avons vu deux écritures principales :
\(A=\begin{pmatrix} x_1 a_1 & x_2 a_1 & \ldots & x_n a_1 \\ x_1 a_2 & x_2 a_2 & \ldots & x_n a_2 \\ \vdots & & & \vdots \\ x_1 a_n & x_2 a_n & \ldots & x_n a_n \end{pmatrix} \) avec \((a_1,…,a_n)\) et \((x_1,…,x_n)\) des réels non tous nuls
OU
\(A=U^tV\).
Il est donc important que tu associes ces écritures à des matrices de rang \(1\) et que tu puisses ainsi utiliser toutes les propriétés que nous avons vues.
De plus, il est important de savoir redémontrer la condition nécessaire et suffisante de diagonalisation d’une matrice de rang \(1\), car c’est une question récurrente aux écrits et aux oraux.
Pour t’entraîner
Pour aller plus loin, tu peux essayer de résoudre les exercices de ce site qui reprennent les démonstrations que nous avons vues dans cet article.
N’hésite pas à consulter toutes nos ressources mathématiques !