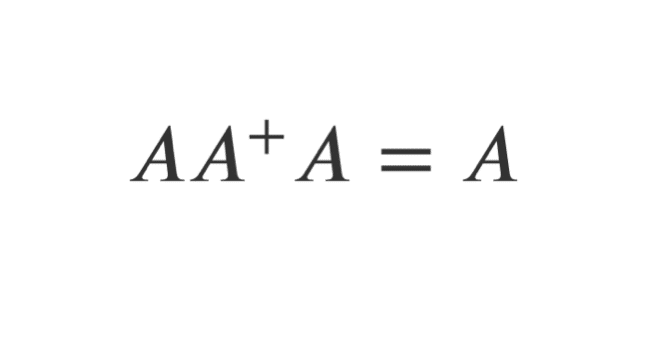Le pseudo-inverse, également connu sous le nom d’inverse généralisé ou encore d’inverse de Moore-Penrose, est une notion fondamentale en mathématiques, notamment en algèbre linéaire. Ce thème généralise l’inverse traditionnel pour les matrices (et les applications linéaires) qui ne sont pas inversibles ou même qui ne sont pas carrées. Le concept d’inverse de Moore-Penrose est particulièrement utile, car il trouve de nombreuses applications dans plusieurs domaines tels que l’optimisation et la régression linéaire. Dans cet article, je te présente l’intérêt et les enjeux de cette notion, ainsi que plusieurs de ses propriétés qui te seront utiles lors de ta préparation aux écrits.
La notion de pseudo-inverse
Certaines matrices carrées (et toutes les matrices rectangulaires) n’admettent pas d’inverse, la notion de pseudo-inverse permet donc d’obtenir un objet mathématique qui s’en rapproche pour ces matrices spéciales.
La multiplication à gauche et à droite d’une matrice \(A\) par son pseudo-inverse est égale à son pseudo-inverse. Un résultat qui est également vrai entre une matrice inversible et son inverse, d’où la proximité de ces notions.
Le pseudo-inverse est utilisé dans divers domaines mathématiques et techniques pour résoudre des problèmes qui n’auraient pas de solution autrement.
Pseudo-inverse d’une matrice et d’une application linéaire
Pseudo-inverse d’une matrice
Soit \( A \in \mathcal{M}_{n,p} (\mathbb{R}) \), alors son pseudo-inverse que l’on notera \(A^+\) (notation usuelle) est l’unique matrice dans \( \mathcal{M}_{p,n} (\mathbb{R}) \) telle que :
- \( AA^+A=A\)
- \( A^+AA^+=A^+\)
- \( {}^t(AA^+)=AA^+\)
- \( {}^t(A^+A)=A^+A\)
Remarque : il y a existence et unicité du pseudo-inverse, c’est-à-dire toute matrice admet un unique pseudo-inverse.
Pseudo-inverse d’une application linéaire
La notion peut se généraliser aux applications linéaires. En effet, considérons \( f : E \to F \) et \( f^+ : F \to E \) deux applications linéaires. Ainsi, \(f^+\) est le pseudo-inverse de \( f \) si et seulement si :
- \( f^+ \circ f \circ f^+ = f^+ \)
- \( f \circ f^+ \circ f = f \)
Quelques propriétés du pseudo-inverse d’une matrice
La pseudo-inversion est involutive
La pseudo-inversion est dite involutive (c’est une application bijective qui est sa propre réciproque). Autrement dit, \( (A^+)^+=A. \) En effet :
- \( A^+(A^+)^+A^+=A^+ \)
- \( (A^+)^+A^+(A^+)^+=(A^+)^+ \)
- \( {}^t(A^+(A^+)^+)=A^+(A^+)^+ \)
- \( {}^t((A^+)^+A^+)=(A^+)^+A^+ \)
Donc : \( (A^+)^+ \) est le pseudo-inverse de \( A^+ \). En utilisant l’unicité du pseudo-inverse et le fait que \(A\) est le pseudo-inverse de \( A^+ \), nous pouvons en déduire que \( (A^+)^+ = A\).
La pseudo-inversion commute avec la transposition
Nous avons que \({}^t(A^+) = ({}^tA)^+. \) Pour démontrer ce résultat, il faut procéder exactement de la même manière que pour la propriété précédente.
Liens entre pseudo-inverse et projecteur orthogonal
Les matrices \(AA^+\) et \(A^+A\) sont des projecteurs orthogonaux. En effet, en utilisant la définition de pseudo-inverse, nous obtenons que :
- \( (AA^+)^2=(AA^+A)A^+=AA^+\; et \; {}^t(AA^+)=AA^+\)
- \( (A^+A)^2=(A^+AA^+)A=A^+A \; et \; {}^t(A^+A)=A^+A\)
Pseudo-inversion et optimisation
L’équation \(AX=B\) d’inconnue \(X\) (avec \(A\) une matrice et \(B\) un vecteur) n’admet pas toujours de solution. Cependant, nous pouvons chercher un vecteur \(X\) qui minimise \( \| AX-B\|. \) La solution de ce problème des moindres carrés est obtenue grâce au pseudo-inverse. En effet, la solution vaut \(A^+B\).
Les pseudo-inverses classiques
Pseudo-inverse d’une matrice inversible
Soit \( A \in GL_n(\mathbb{R}), \) alors \( A^+ = A^{-1}. \) En effet :
- \( A^{-1}AA^{-1} = I_n A^{-1} = A^{-1} \)
- \( AA^{-1}A = I_nA = A \)
- \( {}^t(AA^{-1})={}^t(I_n)=I_n=AA^{-1} \)
- \( {}^t(A^{-1}A)={}^t(I_n)=I_n=A^{-1}A \)
Pseudo-inverse d’un vecteur colonne
Soit \( X \in \mathcal{M}_{n,1}(\mathbb{R}) \) tel que \(X\) n’est pas le vecteur nul. Alors : \( X^+ = \displaystyle \frac{{}^tX}{\| X\|^2}.\) Cela se démontre comme dans l’exemple ci-dessus.
Pseudo-inverse d’une matrice diagonalisable
Soient \( A \) une matrice diagonalisable de \( \mathcal{M}_{n}(\mathbb{R}), \lambda_1, …, \lambda_n \) une liste étendue de ses valeurs propres et \(P\) une matrice orthogonale telle que \(A=P\text{Diag}(\lambda_1, …, \lambda_n ){}^tP. \) De plus, considérons la fonction \(f : x \in \text{Sp}(A)\to \begin{cases}
0 &\text{si} \; x = 0\\
\displaystyle \frac{1}{x} &\text{sinon} \end{cases}
\)
Ainsi : \( A^+ = P\text{Diag}( f(\lambda_1), …, f(\lambda_n )){}^tP \)
Pseudo-inverse de la matrice nulle
La matrice nulle est l’exemple classique qui te permet de montrer que toutes les matrices carrées ne sont pas inversibles en utilisant son caractère absorbant. Cependant, cette matrice ne fait pas exception à la propriété que nous avons énoncée ci-dessus. C’est-à-dire que toute matrice admet un pseudo-inverse.
Ainsi, la matrice nulle est aussi l’exemple classique qui te permet de montrer qu’une matrice carrée non inversible peut avoir un pseudo-inverse qui est d’ailleurs la matrice nulle (cela se démontre en utilisant la définition du pseudo-inverse).
Conclusion
En résumé, le pseudo-inverse d’une matrice est un outil mathématique précieux en algèbre linéaire avec des applications diverses et concrètes. Bien que hors programme, sa compréhension approfondie enrichira tes connaissances et tes compétences en algèbre. Ce qui te permettra d’être plus performant(e) à toutes les épreuves de mathématiques !
Pour t’entraîner sur ce thème, tu peux t’exercer sur des sujets (mathématiques approfondies) :
Tu peux retrouver ici toutes nos autres ressources mathématiques !