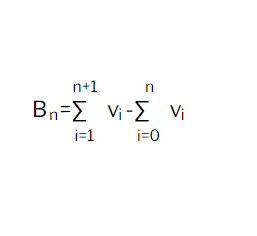Dans cet article, je te propose quatre astuces pour déterminer rapidement la nature d’une série. Beaucoup d’élèves ne pensent pas directement à ces astuces lorsqu’ils sont confrontés à des questions sur les séries, c’est pourquoi je te conseille de les avoir en tête, afin de faire la différence en gagnant des points facilement.
Si tu as besoin d’une petite piqûre de rappel sur les différentes méthodes pour trouver la nature d’une série, n’hésite pas à consulter cet article.
Astuce 1 : Prouver la convergence en utilisant la parité des termes
Si on sépare la série en deux morceaux (l’un des morceaux étant formé par les termes pairs et l’autre par les termes impairs) et que ces deux morceaux convergent chacun, alors on peut en déduire la convergence de la série.
Réciproquement, si une série converge, on peut aussi prouver la convergence de chacun des deux morceaux, comme on va le voir ci-dessous.
Exemple
Nature et calcul de \(\displaystyle \sum_{k=0}^{n} \frac{x^{2k}}{(2k)!}\) et de \(\displaystyle \sum_{k=0}^{n} \frac{x^{2k+1}}{(2k+1)!}\)
Rappel de cours : la série exponentielle \(\displaystyle \sum_{k=0}^{n}\frac{ x^{k}}{k!}\) converge et sa somme vaut \(e^{x}\).
On note \(S_1\) la série composée des termes pairs de la série exponentielle et \(S_2\) celle des termes impairs.
\(S_1\)= \(\displaystyle \sum_{k=0}^{n} x^{2k}/(2k)!\) \(S_2\)=\(\displaystyle \sum_{k=0}^{n} x^{2k+1}/(2k+1)!\)
\(S_1+S_2\)=\(1+x^{2}/2!+x^{4}/4!+…+x^{2n}/(2n)!+x+x^{3}/3!+…+x^{2n+1}/(2n+1)!\)
= \(\displaystyle \sum_{k=0}^{2n+1} x^{k}/(k)!\)
Or, on sait que \(x^{k}/k!\) est le terme général d’une série exponentielle qui converge et de somme \(e^{x}\). Donc \(S_1+S_2\) converge et sa somme vaut \(e^{x}\).
\(S_1-S_2\)=\(1+x^{2}/2!+x^{4}/4!+…+x^{2n}/(2n)!-x-x^{3}/3!-…-x^{2n+1}/(2n+1)!\)
=\(\displaystyle \sum_{k=0}^{2n+1} (-1)^{k} x^{k}/(k)!\)
Or, on sait que \((-x)^{k}/(k)!\) est le terme général d’une série exponentielle qui converge et de somme \(e^{-x}\). Donc \(S_1-S_2\) converge et sa somme vaut \(e^{-x}\).
On remarque aussi que : \(S_1=[(S_1+S_2)+(S_1-S_2)]/2\) \(S_2=[(S_1+S_2)-(S_1-S_2)]/2\)
Par combinaison linéaire de séries convergentes, on en déduit que \(S_1\) et \(S_2\) convergent. On peut aisément trouver la valeur de leur somme :
\(S_1=(e^{x}+e^{-x})/2\) \(S_2=(e^{x}-e^{-x})/2\)
Astuce 2
Utiliser \(k=k+1-1\) et \(k^2=(k+1-1)k=k(k-1)+k\)
Cette astuce n’est pas seulement valable pour les séries et peut être utile dans différents chapitres.
Dans le cas des séries, elle permet de séparer la série en plusieurs morceaux. Si chaque morceau converge, alors la série converge.
Exemple
Nature et calcul de \(\displaystyle \sum_{k=1}^{n}(k^2+1)/k!\)
On sépare la série en deux morceaux :
\(\displaystyle \sum_{k=1}^{n}(k^2+1)/k! = (\displaystyle \sum_{k=1}^{n}k^2/k!) +(\displaystyle \sum_{k=1}^{n}1/k!)\)
On reconnaît que \(\displaystyle \sum_{k=1}^{n}1/k!\) est une série exponentielle qui converge de somme \(e^{1}\).
De plus, \(\displaystyle \sum_{k=1}^{n}k^2/k! =(\displaystyle \sum_{k=1}^{n}k/(k-1)!)\).
On utilise alors l’astuce \(k=k-1+1\), on a donc : \(\displaystyle \sum_{k=1}^{n}(k-1)/(k-1)!)+(\displaystyle \sum_{k=1}^{n}1/(k-1)!)\)
Or, \((\displaystyle \sum_{k=1}^{n}(k-1)/(k-1)!)=\displaystyle \sum_{k=2}^{n}1/(k-2)!\)
Ainsi : \(\displaystyle \sum_{k=1}^{n}(k^2+1)/k!\)=\((\displaystyle \sum_{k=1}^{n}1/k!)+(\displaystyle \sum_{k=2}^{n}1/(k-2)!)+(\displaystyle \sum_{k=1}^{n}1/(k-1)!)\)
La série à calculer peut dont être découpée en trois séries exponentielles qui convergent toutes, la série converge donc.
On peut en déduire sa somme : \(\displaystyle \sum_{k=1}^{+\infty}(k^{2}+1)/k!\)=\(\displaystyle \sum_{k=2}^{+\infty}1/(k-2)!\)+\(\displaystyle \sum_{k=1}^{+\infty}1/(k-1)!\)+\((\displaystyle \sum_{k=1}^{+\infty}1/k!)\)
On fait deux changements d’indices en posant \(i=k-2\) et \(j=k-1\)
Ainsi, on trouve : \(\displaystyle \sum_{k=1}^{n}(k^2+1)/k!=e+e+e-1=3e-1\)
Astuce 3 : Faire des télescopages
Lorsqu’il y a des questions concernant des sommes, il est très courant d’avoir recours au télescopage. Tu verras aussi qu’il est fréquent (mais pas toujours nécessaire) d’effectuer un changement d’indice sur la somme avant le télescopage.
Beaucoup de questions « classiques » demandent de prouver la convergence d’une suite donnée grâce à un télescopage effectué sur une série dont le terme général est construit à l’aide des termes de la suite en question. En voici un exemple.
Exemple
Montrer par double implication que la suite \((v_n)\) converge si la série de terme général \(v_{n+1}- v_n\) converge.
On note \(B_n\) la série de terme général \(v_{n+1}- v_n\).
\(B_n\)=\(\displaystyle \sum_{k=0}^{n}v_{k+1}-v_k\)
La série converge, donc on peut utiliser la linéarité de la somme : \(B_n\)=\(\displaystyle \sum_{k=0}^{n}v_{k+1}\)-\(\displaystyle \sum_{k=0}^{n}v_k\)
Avec un changement d’indice, on pose \(i=k+1\). On a donc : \(B_n\)=\(\displaystyle \sum_{i=1}^{n+1}v_{i}\)-\(\displaystyle \sum_{i=0}^{n}v_i\)
Par télescopage, on a : \(B_n\)=\(v_{n+1}-v_0\)
Or, comme on sait que la série converge, on peut noter \(a\) sa limite et on peut écrire : \(\exists a \in \mathbb{R}, \lim \limits_{n \to +\infty} v_{n+1}-v_0=a \)
Donc : \(\lim \limits_{n \to +\infty} v_{n+1}=a+v_0\)
Et par unicité de la limite, on a : \(\lim \limits_{n \to +\infty} v_n=a+v_0\)
Ainsi, \(v_n\) converge.
Astuce 4 : Utiliser la définition de la limite d’une suite
Pour prouver qu’une série converge, on utilise très souvent le critère de comparaison des séries à termes positifs.
Parfois, utiliser la définition de la limite d’une suite peut être utile afin de trouver l’encadrement du terme général de la suite qui servira à appliquer le critère de comparaison.
Exemple
Sachant que \(\sum_{n \in \mathbb{N}} w_n\) converge, montrer que \(\sum_{n \in \mathbb{N}} (w_n)^2\) converge.
Comme la série de terme général \(w_n\) converge, \(\lim \limits_{n \to +\infty} w_n=0\).
D’après la définition de la limite : \(\exists n_o \in\mathbb{N}, \forall n\ge n_0, w_n<1\)
Alors, on a aussi : \(\forall n\ge n_0, 0\le (w_n)^2\le w_n\)
Ainsi, d’après le critère de comparaison des séries à termes positifs, comme\(\sum_{n \in \mathbb{N}} w_n\) converge, on a \(\sum_{n \in \mathbb{N}} (w_n)^2\) qui converge.
Conclusion
L’article touche à sa fin, j’espère qu’il t’aura été utile. Tu veux apprendre comment appréhender et intérioriser toutes ces astuces ? Alors consulte le carnet d’astuces en maths : une bonne idée ?
N’hésite pas à consulter toutes nos autres ressources mathématiques !