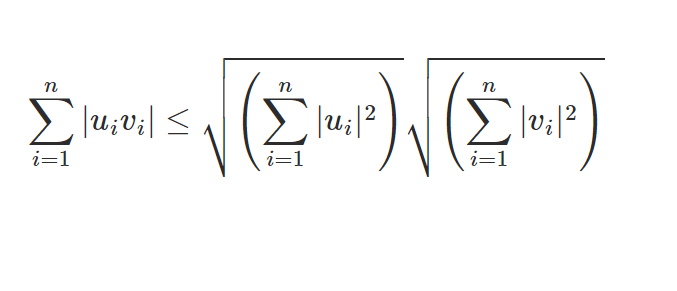On va se pencher sur cinq questions classiques utilisant l’inégalité de Cauchy-Schwarz. On la retrouve principalement dans les sujets de maths EDHEC et emlyon (ou encore Ecricome), mais aussi parfois dans des sujets de Parisiennes. Cette inégalité peut être rencontrée aussi bien dans des sujets d’algèbre que dans des sujets d’analyse, ou encore de probabilités. Ces questions sont des points à prendre facilement, il est important de savoir les repérer rapidement.
Petit rappel de l’inégalité de Cauchy-Schwarz
Soit \((u_1,u_2,…,u_3)\) et \((v_1,v_2,…,v_n)\), deux vecteurs de \(R^n\).
\(\displaystyle \sum_{i=1}^n\vert u_iv_i\vert\leq \sqrt{\left(\sum_{i=1}^n\vert u_i\vert^2\right)} \sqrt{\left(\sum_{i=1}^n\vert v_i\vert^2\right)}\)
avec égalité si et seulement s’il existe \(\lambda\in\mathbb R\) tel que \(|u_i|=\lambda |v_i|\) pour tout \(i=1,2,…n\).
Fonctions à plusieurs variables et recherche d’extremums
Dans les exercices d’analyse portant sur les fonctions à plusieurs variables, tu seras souvent amené(e) à utiliser l’inégalité de Cauchy-Schwarz pour trouver l’extremum de la fonction (minimum ou maximum).
Voici un exemple extrait du sujet EDHEC 2018 ECS (épreuve annulée) : exercice 3, somme harmonique, question 4.b.
Question 1
Pour tout (\(x_1, x_2,…,x_n)\) appartenant à \(R^n\), montrer que :
\(\left(\displaystyle \sum_{k=1}^{n}x_k \right)^2\)\(\le\)n \(\left(\displaystyle \sum_{k=1}^{n}x_k^2 \right)\)
Commentaires
Pour utiliser l’inégalité correctement, il faut d’abord se poser plusieurs questions :
- Quel produit scalaire canonique va-t-on utiliser ?
- Sous quelle forme faut-il utiliser l’inégalité ? Penser à élever au carré.
- À quels vecteurs va-t-on appliquer Cauchy-Schwarz ?
Corrigé
On choisit le produit scalaire canonique de \(R^n\).
On note \(A\) et \(B\) deux vecteurs de \(R^n\) tels que : \(A\) = \((x_1,x_2,…,x_n)\) et \(B\) = \((1,1,…,1)\).
On applique l’inégalité de Cauchy-Schwarz à ces deux vecteurs, ce qui donne :
\((\displaystyle \sum_{k=1}^{n}x_k)^2 \le (\displaystyle \sum_{k=1}^{n}x_k^2 ) (\displaystyle \sum_{k=1}^{n}1^2) = (\displaystyle \sum_{k=1}^{n}x_k^2 ) n\)
Ainsi : \(\left(\displaystyle \sum_{k=1}^{n}x_k \right)^2\le n\left(\displaystyle \sum_{k=1}^{n}x_k^2 \right)\)
Pour vérifier que tu as bien compris, voici une deuxième question sur l’inégalité de Cauchy-Schwarz dans les fonctions à plusieurs variables, extraite de EDHEC 2010 (ECS), exercice 1 question 6.
Question 2
Soit \(n \ge 2\). On considère la fonction \(f_n\) définie, pour tout \((x_1,x_2,…,x_n)\) de l’ouvert U=\((\mathbb{R}_{+}^{*}\) \(^n)\) par \(f_n(x_1,…,x_n\))=\(\left(\displaystyle \sum_{k=1}^{n}x_k \right)\)\(\left(\displaystyle \sum_{k=1}^{n}1/x_k \right)\)
Étude du cas général
On considère l’espace euclidien \(R^n\) muni de son produit scalaire canonique. En appliquant l’inégalité de Cauchy-Schwarz à deux vecteurs bien choisis de \(R^n\), montrer que \(f_n\) admet un minimum global sur U, égal à \(n^2\).
Commentaires
Après avoir repéré le bon produit scalaire, il faut bien choisir les vecteurs (pense à utiliser la racine carrée). Enfin, bien sûr, utilise Cauchy-Schwarz.
Corrigé
Algèbre bilinéaire et endomorphismes symétriques
Dans les exercices d’algèbre bilinéaire, il est courant d’utiliser cette inégalité. Comme les endomorphismes peuvent être associés à des matrices, il faudra penser à utiliser parfois un produit scalaire matriciel.
Voici deux questions d’algèbre mettant en jeu Cauchy-Schwarz. Pour te montrer que ces questions peuvent se retrouver dans des sujets de difficultés variées, la première est extraite d’Ecricome 2017, question 3 (ECS) et la deuxième de Maths I 2019, Partie II, question c (ECS).
Question 3
\(A\) est une matrice de \(\mathcal{M}_{n}(\mathbb{R})\) qui est symétrique et dont toutes les valeurs propres sont strictement positives. On note \(u\) l’endomorphisme de \(R^n\) dont \(A\) est la matrice dans la base canonique de \(R^n\).
Après avoir montré que \(A\) est diagonalisable et qu’il existe une matrice \(B\) de \(\mathcal{M}_{n}(\mathbb{R})\) telle que \(B^2\)=\(A\), on note \(v\) l’endomorphisme, dont \(B\) est la matrice dans la base canonique de \(R^n\).
À l’aide de \(v\) et de l’inégalité de Cauchy-Schwarz, montrer que : \(\forall (x ,y)\in(\mathbb{(R^n)}^2)\) \(\langle x,y\rangle)^2\)\(\le\) \(\langle u(x),x\rangle)\) \(\langle u^{-1}(y),y\rangle\).
Commentaires
Sachant que \(B\) est inversible, v l’est aussi, il faut essayer d’utiliser l’inversibilité de \(v\) pour réécrire \(y\).
Il faut ensuite utiliser le fait que \(v\) soit un endomorphisme symétrique.
Enfin, il faut utiliser Cauchy-Schwarz.
Corrigé
Question 4
Rappeler l’inégalité de Cauchy-Schwarz, puis vérifier que :
\(\forall A \in (\mathcal{M}_{n}(\mathbb{R}))\), \(\text{Tr}(A^{2}) \)\(\le\)\(\text{Tr}({}^tAA)\)
Commentaires
- Quel produit scalaire matriciel utiliser ?
- Essayer d’écrire la norme de \(A\) au carré avec les coefficients et trouver une relation entre la norme de \(A\) et de sa transposée.
- Utiliser Cauchy-Schwarz.
Probabilités
Enfin, pour te montrer à quel point cette notion est transversale et peut aussi bien se retrouver dans des exercices d’analyse que d’algèbre et de probas, voici une dernière question. Cette fois, une question de probabilités.
Question 5
Soit \(X\) une variable aléatoire réelle qui prend ses valeurs dans \(\mathbb{N}^{*}\). On suppose que \(X\) a une espérance. Montrer que : 1 \(\le\)\(E(X)\)\(E(1/X)\)
Commentaires
- Penser à faire passer le \(E(X)\) de l’autre côté de l’inégalité.
- Prouver que les deux variables possèdent une espérance et les exprimer sous forme de série.
- Bien choisir les vecteurs (penser au choix des vecteurs de l’exercice 2).
- Appliquer Cauchy-Schwarz.
Corrigé
L’inégalité peut se réécrire comme telle : \(1/E(X)\le E(1/X)\)
Comme \(X\) et \(1/X\) sont bornées, elles admettent chacune une espérance.
\(E(X)\)=\(\displaystyle \sum_{k=1}^{+\infty} kP(X=k)\) \(E(1/X)\)=\(\displaystyle\sum_{k=1}^{+\infty} 1/k P(X=k)\)
Soit \(A\) et \(B\) deux vecteurs de \(R^n\), tels que \(A\)= \(\sqrt{kP(X=k)}_{1 \le k \le n}\) et \(B\)= \(\sqrt{(1/k)P(X=k)}_{1 \le k \le n}\)
On applique l’inégalité de Cauchy-Schwarz à ces deux vecteurs, on a donc :
\((\displaystyle \sum_{k=1}^{n}P(X=k))^2\)\(\le\) \((\displaystyle \sum_{k=1}^{n}k P(X=k)) (\displaystyle \sum_{k=1}^{n}(1/k)P(X=k))\)
Comme les espérances existent, on sait que les séries convergent.
On peut donc utiliser le théorème de conservation des inégalités par passage à la limite quand \(n\) tend vers \(+\infty\).
Ainsi : \(1\le E(X) E(1/X)\)
Conclusion
Cet article touche à sa fin, j’espère qu’il te sera utile ! N’hésite pas à refaire régulièrement ces questions. La répétition est vraiment une des clés pour réussir en maths.
Tu peux aussi consulter nos autres ressources si ça t’intéresse.