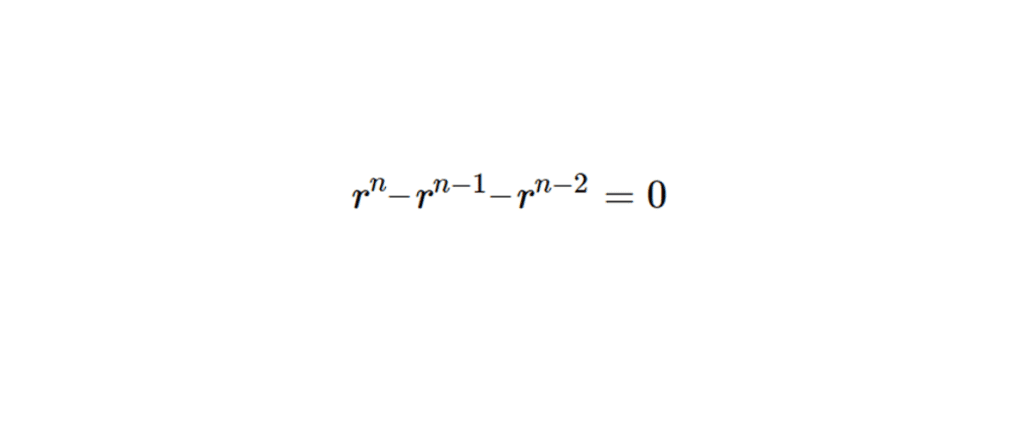La suite de Fibonacci est l’une des suites les plus célèbres en mathématiques, non seulement pour sa simplicité apparente, mais aussi pour ses profondes implications dans divers domaines. Dans cet article, nous allons explorer la récurrence de Fibonacci, c’est-à-dire la relation mathématique qui définit cette suite, et découvrir comment elle conduit au nombre d’or, ainsi que ses nombreuses applications. La suite de Fibonacci est une notion hors programme ECG qui est très en vogue ces derniers temps et pourrait faire l’objet d’un sujet de maths aussi bien aux écrits qu’aux oraux.
Rappel sur la suite de Fibonacci
Avant de plonger dans les détails de la récurrence, rappelons brièvement ce qu’est la suite de Fibonacci. Cette suite est définie par les deux premiers termes \( F_0 = 0 \) et \( F_1 = 1 \), et chaque terme suivant est obtenu en additionnant les deux termes qui le précèdent :
\[
F_n = F_{n-1} + F_{n-2} \quad \text{pour } n \geq 2
\]
Ainsi, les premiers termes de la suite de Fibonacci sont : 0, 1, 1, 2, 3, 5, 8, 13, 21, etc.
Cette simple règle de récurrence a entraîné de nombreuses recherches depuis des siècles en raison de ses propriétés fascinantes et de ses apparitions dans des contextes aussi variés que la biologie, l’architecture et l’art.
La relation de récurrence : une suite linéaire d’ordre 2
La récurrence de Fibonacci est une suite récurrente linéaire d’ordre 2. Cela signifie que chaque terme de la suite est une combinaison linéaire des deux termes précédents. En termes mathématiques, la relation de récurrence peut être exprimée comme suit :
\[
F_n = F_{n-1} + F_{n-2}
\]
Cette relation est dite d’ordre 2, car elle implique deux termes précédents pour déterminer le terme actuel. Une autre caractéristique clé de cette récurrence est sa linéarité, c’est-à-dire que les coefficients des termes précédents sont des constantes (ici, 1 pour \( F_{n-1} \) et \( F_{n-2} \)).
Pour mieux comprendre cette récurrence, analysons-la en détail et découvrons comment elle nous conduit à une découverte fascinante : le nombre d’or.
Résolution de la récurrence et apparition du nombre d’or
Pour résoudre la récurrence de Fibonacci, on cherche une solution générale sous la forme \( F_n = r^n \), où \( r \) est une constante à déterminer. Substituons cette forme dans l’équation de récurrence :
\[
r^n = r^{n-1} + r^{n-2}
\]
En simplifiant, on obtient :
\[
r^n – r^{n-1} – r^{n-2} = 0
\]
En divisant par \( r^{n-2} \) (étant donné que \( r \neq 0 \)), on a :
\[
r^2 – r – 1 = 0
\]
Cette équation quadratique est appelée l’équation caractéristique de la récurrence de Fibonacci. Les solutions de cette équation sont :
\[
r_{1,2} = \frac{1 \pm \sqrt{5}}{2}
\]
Les deux solutions \( \displaystyle r_1 = \frac{1 + \sqrt{5}}{2} \) et \( \displaystyle r_2 = \frac{1 – \sqrt{5}}{2} \) sont les racines caractéristiques de la récurrence. La première racine \( r_1 \) est connue sous le nom de nombre d’or, souvent noté \( \varphi \) (phi), qui vaut environ 1,618. La seconde racine, \( r_2 \), est son inverse, souvent noté \( \overline{\varphi} \), qui est un nombre négatif d’une valeur absolue inférieure à 1.
La solution générale de la récurrence est donc une combinaison linéaire des puissances de ces racines :
\[
F_n = A \cdot \varphi^n + B \cdot \overline{\varphi}^n
\]
Où \( A \) et \( B \) sont des constantes déterminées par les conditions initiales \( F_0 \) et \( F_1 \). En utilisant ces conditions, on trouve que \( \displaystyle A = \frac{1}{\sqrt{5}} \) et \( \displaystyle B = -\frac{1}{\sqrt{5}} \).
Ainsi, la formule explicite pour les termes de la suite de Fibonacci est :
\[
F_n = \frac{1}{\sqrt{5}} \left( \varphi^n – \overline{\varphi}^n \right)
\]
Cette formule que nous venons d’obtenir grâce à la relation de récurrence qui définit la suite de Fibonacci est connue sous le nom de Formule de Binet.
Ce résultat montre comment la simple règle de récurrence de Fibonacci est intimement liée au nombre d’or, une constante qui apparaît fréquemment dans la nature et l’art.
Une perspective matricielle sur la récurrence de Fibonacci
Pour approfondir la compréhension de la récurrence de Fibonacci, on peut la reformuler en termes de matrices, ce qui offre une nouvelle perspective sur sa dynamique. Considérons un vecteur colonne \( \mathbf{u}_n = \begin{pmatrix} F_n \\ F_{n-1} \end{pmatrix} \). La relation de récurrence peut alors s’exprimer par le produit matriciel suivant :
\[
\mathbf{u}_{n+1} = \begin{pmatrix} F_{n+1} \\ F_n \end{pmatrix} = \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} F_n \\ F_{n-1} \end{pmatrix} = \mathbf{M} \cdot \mathbf{u}_n
\]
Ici, \( \mathbf{M} = \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix} \) est la matrice de transition associée à la suite de Fibonacci. Cette formulation permet d’analyser l’évolution de la suite en examinant les propriétés de cette matrice.
Pour explorer la dynamique de la suite, nous cherchons les valeurs propres de \( \mathbf{M} \). Ces valeurs propres \( \lambda_1 \) et \( \lambda_2 \) sont les solutions de l’équation caractéristique de \( \mathbf{M} \) :
\[
\det(\mathbf{M} – \lambda \mathbf{I}) = 0
\]
Cela donne l’équation quadratique suivante :
\[
\lambda^2 – \lambda – 1 = 0
\]
Les solutions de cette équation, \( \displaystyle \lambda_1 = \frac{1 + \sqrt{5}}{2} \) et \( \displaystyle \lambda_2 = \frac{1 – \sqrt{5}}{2} \), correspondent respectivement au nombre d’or \( \varphi \) et à son conjugué \( \overline{\varphi} \).
La valeur propre \( \lambda_1 = \varphi \), qui est positive et plus grande que 1, domine le comportement asymptotique de la suite, tandis que \( \lambda_2 = \overline{\varphi} \) est plus petite en valeur absolue et tend vers 0 au fur et à mesure que \( n \) augmente. Par conséquent, à long terme, les termes de la suite de Fibonacci croissent approximativement comme une puissance du nombre d’or \( \varphi^n \).
Cette analyse matricielle illustre comment la structure interne de la récurrence de Fibonacci est intrinsèquement liée aux propriétés algébriques du nombre d’or. En utilisant les outils de l’algèbre linéaire, on met en évidence le rôle fondamental que joue cette constante dans l’évolution de la suite, offrant ainsi une perspective plus profonde sur la nature de cette récurrence.
Pourquoi la récurrence de Fibonacci est partout
La règle selon laquelle chaque terme est la somme des deux précédents a une conséquence fascinante : elle engendre une croissance qui reflète des structures naturelles efficaces. Le fait que la suite de Fibonacci soit présente dans tant de contextes s’explique par la nature même de cette récurrence.
Lorsque les termes sont ajoutés pour former les suivants, chaque nouveau terme porte en lui une partie de l’histoire des termes précédents, ce qui crée une structure autosimilaire. C’est cette propriété qui explique pourquoi on retrouve la suite de Fibonacci dans les spirales des coquillages, la disposition des feuilles sur une tige et même dans certains motifs de croissance des populations.
En effet, dans ces contextes, la croissance optimale est souvent dictée par des contraintes, où chaque élément doit s’ajuster en fonction des éléments précédents, tout en maximisant l’efficacité et l’utilisation de l’espace. La suite de Fibonacci, avec sa relation de récurrence simple mais puissante, offre un modèle idéal pour de tels phénomènes.
Aller plus loin
La suite de Fibonacci est à l’origine de nombreuses recherches et nombreux problèmes mathématiques. Pour y voir plus clair, voici une cartographie de l’ensemble des recherches tournant autour de la suite de Fibonacci (et du nombre d’or) :
| Tableau de correspondances suites/nombres (en lien avec Fibonacci/nombres métalliques) |
|
| Suites | Nombres |
| Suite de Fibonacci | Nombre d’or |
| Suite de Pell | Nombre d’argent |
| Généralisation de Fibonacci : les suites k-bonacci | Nombres métalliques : généralisation du nombre d’or |
| Suite de Lucas | Nombre de Lucas |
| Suite de Padovan | Nombre plastique |
| Suite de Perrin | Nombres pseudo-premiers de Perrin |
| Suite de Jacobsthal | Nombres oblongs de Jacobsthal |
| Polynôme/suite de Narayana | Nombre de Narayana |
| Nombre de Gildas | |
| Nombre de Keith | |
| Super nombre d’or | |
Un autre type de généralisation de la suite de Fibonacci est également à découvrir ! Il s’agit de la suite de Fibonacci aléatoire. Elle pourrait clairement faire l’objet d’un sujet de maths parisienne dans les années à venir…
A lire également : le triangle de Pascal (et ses liens avec la suite de Fibonacci).
Conclusion
La récurrence de Fibonacci, au-delà de sa simplicité apparente, cache des richesses mathématiques qui ont fasciné les esprits pendant des siècles. À travers la résolution de cette récurrence, nous avons vu comment elle est reliée au nombre d’or, un symbole de perfection esthétique et de croissance naturelle. En outre, la structure même de cette récurrence explique pourquoi la suite de Fibonacci apparaît si fréquemment dans la nature et les œuvres humaines.
Que ce soit dans un contexte purement mathématique ou dans l’observation des phénomènes naturels, la récurrence de Fibonacci reste un exemple fascinant de la manière dont les mathématiques peuvent dévoiler les structures sous-jacentes du monde qui nous entoure.
Ainsi, bien que cette notion soit hors programme, la compréhension approfondie de cette dernière te permettra d’améliorer des compétences en analyse et en algèbre linéaire te préparant donc pour les épreuves écrites et orales. Pour t’entraîner sur cette notion, tu peux réaliser les sujets suivants :
- Ecricome 2018 (mathématiques approfondies),
- Maths 1 HEC 2009 (mathématiques appliquées),
- la première Question Sans Préparation des Oraux HEC 2023.
Tu peux retrouver le méga-répertoire qui contient toutes les annales de concours et les corrigés ! Tu peux également accéder à toutes nos autres ressources mathématiques !