Les notions hors programme se destinent surtout aux candidats qui visent les trois Parisiennes. Cet article te propose de décortiquer le principe des régressions linéaires simples et multiples et d’en comprendre les utilisations. Ce principe est notamment utile en statistiques afin de créer des modèles expérimentaux. Mais il peut également être utilisé en probabilité pour trouver un lien linéaire entre deux variables aléatoires et expliciter une variable en fonction d’une autre.
Dans tout l’article, soit \(n \in
\mathbb{N}\).
Régressions linéaires : principe
Les régressions linéaires ont pour but de trouver une droite ou un polynôme afin de créer un modèle statistique à partir de points donnés. La droite de régression linéaire est alors la droite que l’on peut tracer dans le nuage de points qui représente au mieux la distribution des points.
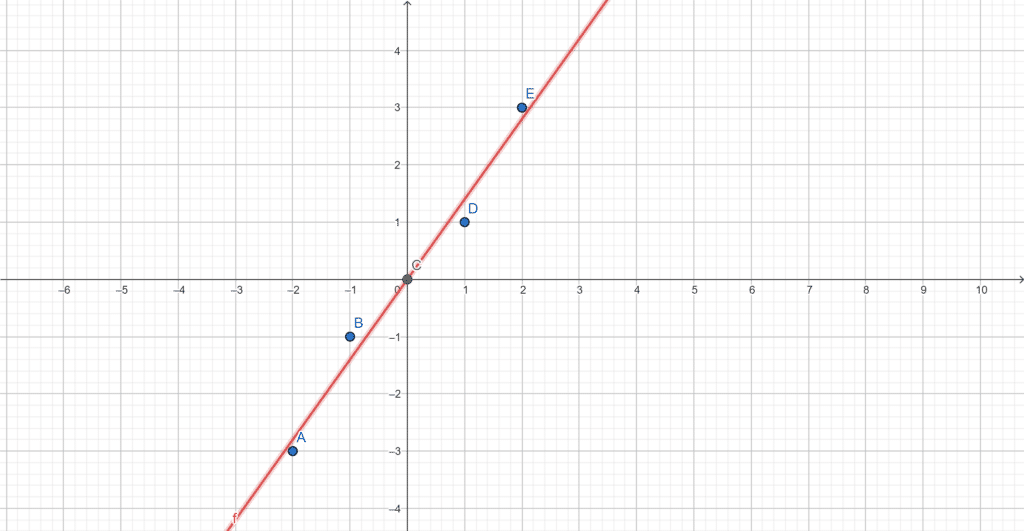
Un graphique est sûrement plus parlant :
Le but de la régression simple est de trouver \(f\) telle que \(\forall i \in [\!
[1,n]\!]\), \(f(x_i) \approx y_i\) avec \(x_i\) et \(y_i\) les abscisses et ordonnées des points étudiés.
Méthode de régression linéaire simple (droite de régression linéaire)
On dispose de \(n\) points \((x_1,y_1)\)…\((x_n,y_n)\) distincts et on cherche à trouver la droite « se faufilant au mieux entre ces points ». On pose \(f:x \mapsto ax+b\) la fonction qui désigne cette droite et on cherche les points \(a\) et \(b\) qui conviennent.
On note \(X=\begin{pmatrix} x_1 \\ \vdots \\
x_n\end{pmatrix}\) et \(Y=\begin{pmatrix} y_1 \\ \vdots \\
y_n\end{pmatrix}\). De même on pose \(Y’=\begin{pmatrix} f(x_1) \\ \vdots \\
f(x_n)\end{pmatrix}\) les sorties dites expérimentales des (\(x_1,…,x_n)\) par le modèle \(f\).
\( Y’= \begin{pmatrix} f(x_1) \\ \vdots \\
f(x_n)\end{pmatrix} = \begin{pmatrix} b+ax_1\\ \vdots \\
b+ax_n\end{pmatrix} = \begin{pmatrix} 1&x_1 \\ 1&x_2 \\ \vdots & \vdots \\ 1&x_n\end{pmatrix} \begin{pmatrix} b \\ a\end{pmatrix}\).
On note \(A=\begin{pmatrix} 1&x_1 \\ 1&x_2 \\ \vdots & \vdots \\ 1&x_n\end{pmatrix}\) et \(U=\begin{pmatrix} b \\ a\end{pmatrix}\). La méthode des moindres carrés nous permet de choisir \(U\) (donc : \(a\) et \(b\)) de façon à ce que le modèle soit le plus précis possible. Cette méthode nous donne alors que \(U\) doit vérifier l’équation : \( {}^tAAU={}^tAY\). Ce résultat est appelé « système d’équations normales ».
\( {}^tAA= \begin{pmatrix} 1&\ldots &1\\ x_1&\ldots &x_n\end{pmatrix} \begin{pmatrix} 1&x_1 \\ 1&x_2 \\ \vdots & \vdots \\ 1&x_n\end{pmatrix} = \begin{pmatrix} n & n \left(\frac{1}{n}\displaystyle \sum_{k=0}^{n} x_k \right) \\ n \left(\frac{1}{n}\displaystyle \sum_{k=0}^{n} x_k \right) & n \left(\frac{1}{n}\displaystyle \sum_{k=0}^{n} (x_k)^2 \right) \end{pmatrix} \).
D’où \({}^tAAU={}^tAY \Leftrightarrow n\begin{pmatrix} 1 & \left(\frac{1}{n}\displaystyle \sum_{k=0}^{n} x_k \right) \\ \left(\frac{1}{n}\displaystyle \sum_{k=0}^{n} x_k \right) & \left(\frac{1}{n}\displaystyle \sum_{k=0}^{n} (x_k)^2 \right) \end{pmatrix} \begin{pmatrix} b \\ a\end{pmatrix} = n \begin{pmatrix} \frac{1}{n}\displaystyle \sum_{k=0}^{n} y_k \\ \frac{1}{n}\displaystyle \sum_{k=0}^{n} x_k y_k \end{pmatrix}\).
Or, le déterminant de \({}^tAA\) est différent de \(0\) si les \((x_1,…,x_n)\) sont distincts, on le note \(d({}^tAA)\). Donc, \({}^tAA\) est inversible.
Alors, \(U=({}^tAA)^{-1}{}^tAY=\frac{1}{n d({}^tAA)}\begin{pmatrix} \left(\frac{1}{n}\displaystyle \sum_{k=0}^{n} (x_k)^2 \right) & -\left(\frac{1}{n}\displaystyle \sum_{k=0}^{n} x_k \right) \\ -\left(\frac{1}{n}\displaystyle \sum_{k=0}^{n} x_k \right) & 1 \end{pmatrix} n \begin{pmatrix} \frac{1}{n}\displaystyle \sum_{k=0}^{n} y_k \\ \frac{1}{n}\displaystyle \sum_{k=0}^{n} x_k y_k \end{pmatrix} \).
Finalement, \(U=\begin{pmatrix} b \\ a\end{pmatrix}=\frac{1}{d({}^tAA)} \begin{pmatrix} \frac{1}{n^2}\displaystyle \sum_{k=0}^{n} (x_k)^2 \displaystyle \sum_{k=0}^{n} y_k – \frac{1}{n^2}\displaystyle \sum_{k=0}^{n} x_k\displaystyle \sum_{k=0}^{n} x_k y_k \\ \frac{1}{n}\displaystyle \sum_{k=0}^{n} x_k y_k – \frac{1}{n^2}\displaystyle \sum_{k=0}^{n} x_k \displaystyle \sum_{k=0}^{n} y_k \end{pmatrix} \).
Une fois que tu as lu cette méthode, les droites de régressions linéaires te paraissent peut-être obscures et difficiles, mais ne t’inquiète pas, avec un exemple, tout va s’éclaircir !
Exemple
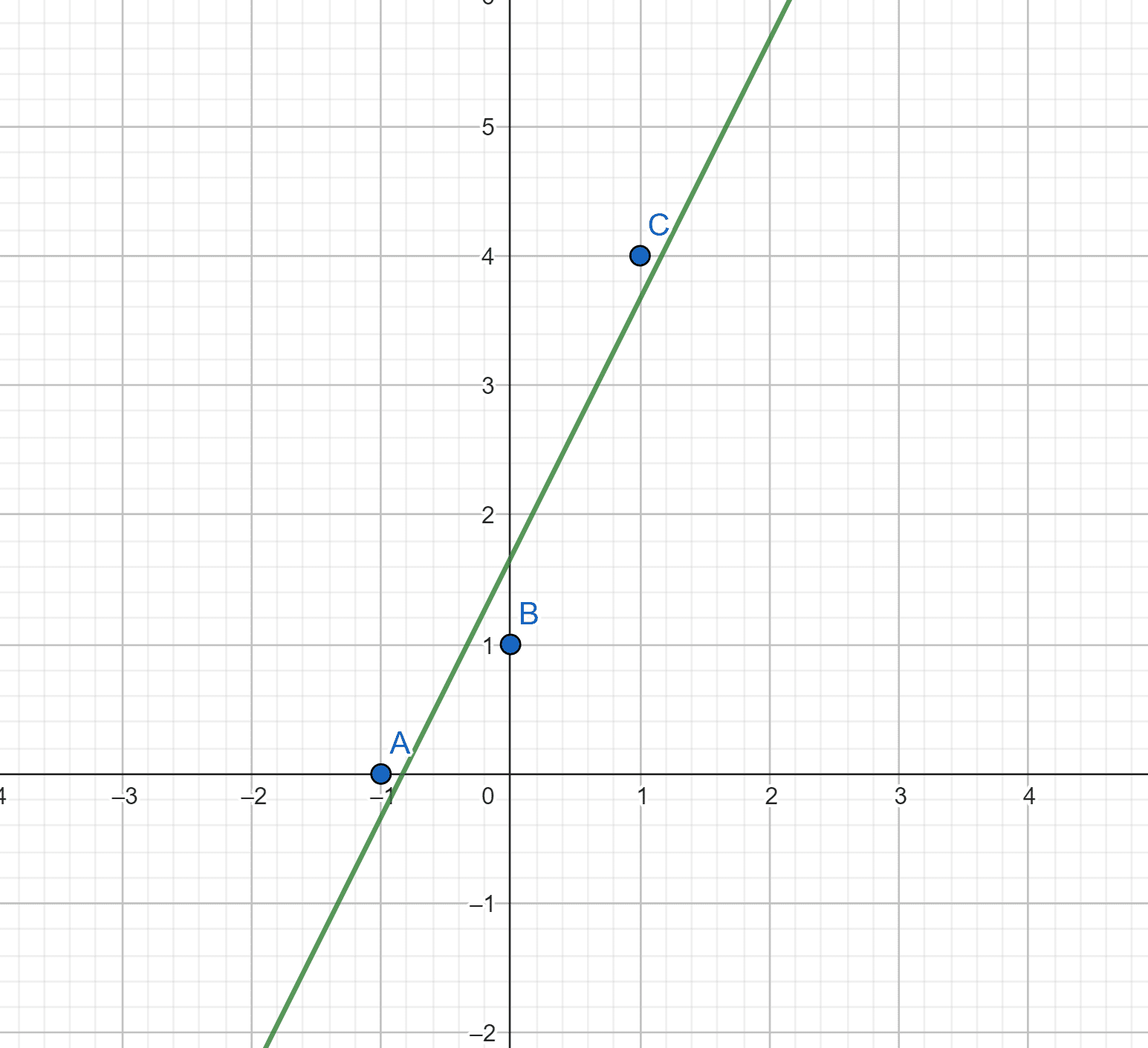
On prend trois points \( (-1,0), (0,1), (1,4)\). On cherche \(U=\begin{pmatrix} b \\ a\end{pmatrix}\).
On a \( A=\begin{pmatrix} 1&-1 \\ 1&0 \\ 1 & 1\end{pmatrix}\) et \( Y=\begin{pmatrix} 0\\ 1 \\4\end{pmatrix}\).
De même \({}^tAA=\begin{pmatrix} 3&0 \\ 0&2 \end{pmatrix}\).
D’où \(\begin{align} {}^tAAU={}^tAY &\Leftrightarrow \begin{pmatrix} 3&0 \\ 0&2 \end{pmatrix}\begin{pmatrix} b \\ a\end{pmatrix} = \begin{pmatrix} 5 \\ 4\end{pmatrix} \\& \Leftrightarrow \begin{pmatrix} b \\ a\end{pmatrix} = \begin{pmatrix} 1/3&0 \\ 0&1/2 \end{pmatrix}\begin{pmatrix} 5 \\ 4\end{pmatrix} \\& \Leftrightarrow U= \begin{pmatrix} 5/3 \\ 2\end{pmatrix}\end{align}\).
La droite recherchée est donc \(f:x \mapsto 2x+5/3\).
En effet, en traçant la courbe et les points, on voit bien que \(f\) se faufile bien au mieux entre les points. Finalement, ce n’est pas si compliqué !
La régression linéaire avec un polynôme
La régression linéaire avec un polynôme suit le même principe. Cependant, au lieu de chercher une droite, il faut trouver un polynôme. On cherche alors les \( (a_0,… a_n)\) tels que \(f:x \mapsto a_0 +a_1 x + a_2 x^2 + … + a_n x^n \).
Le vecteur \(Y\) contient toujours les ordonnées des points, \(U= \begin{pmatrix} a_0\\ a_1 \\ \vdots \\
a_n\end{pmatrix}\) et \(A=\begin{pmatrix} 1 & x_1 & \ldots
& x_1^n \\ 1 & x_2 & \ldots &
x_2^n \\ \vdots & \vdots & & \vdots \\ 1
& x_n & \ldots & x_n^n \end{pmatrix}\), si les \((x_1,…, x_n)\) sont deux à deux distincts, alors \(A\) est une matrice de Vandermonde et vérifie des propriétés bien particulières, que tu peux retrouver ici.
Pour autant, \(U\) doit toujours vérifier le système d’équations normales, c’est-à-dire, \(U\) doit vérifier \({}^tAAU={}^tAY\).
Exemple
On dispose de quatre points \( (-1,0), (0,1), (1,4), (2,6) \) et on cherche \(f:x \mapsto a_0 +a_1 x + a_2 x^2 \).
On a \(U= \begin{pmatrix} a_0\\ a_1 \\a_2 \end{pmatrix}\), \(A=\begin{pmatrix} 1 & -1 & 1\\ 1 & 0 & 0 \\1 & 1 & 1\\ 1 & 2 & 4 \end{pmatrix}\) et \(Y= \begin{pmatrix} 0\\ 1 \\4 \\6 \end{pmatrix}\).
\({}^tAA=\begin{pmatrix} 4 & 2 & 6\\ 2 & 6 & 8 \\6 & 8 & 18 \end{pmatrix}\) est bien inversible car son rang vaut \(3\).
Donc, \(U=({}^tAA)^{-1}{}^tAY= \begin{pmatrix} 1.45 \\ 1.85 \\ 0.25 \end{pmatrix}\).
Finalement, \(f:x \mapsto 1.45 +1.85x + 0.25 x^2 \).
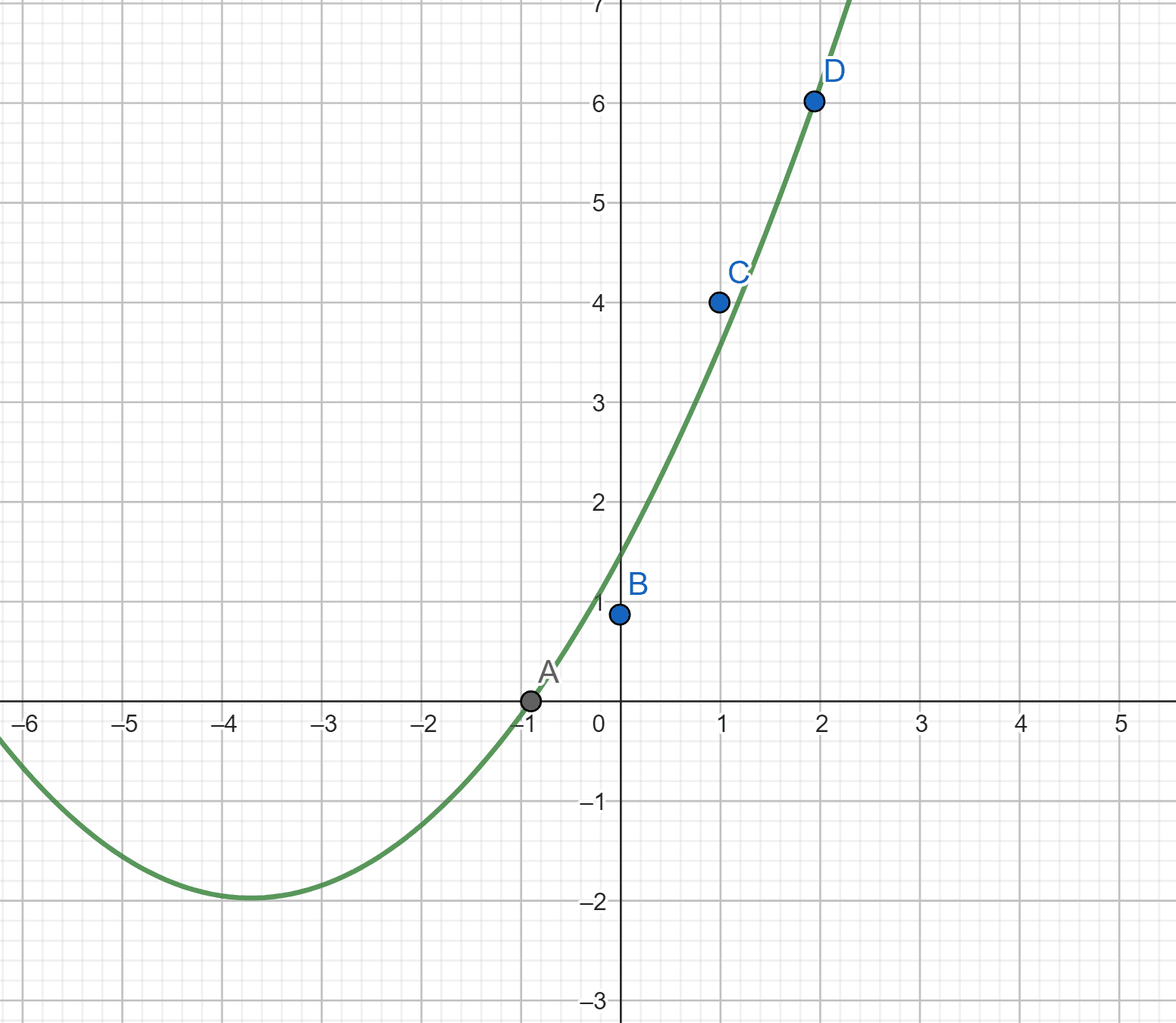
Pour les polynômes de degrés supérieurs, la méthode reste la même, il suffit d’adapter les tailles des matrices.
La régression linéaire multiple
Il s’agit d’une généralisation du modèle de régression linéaire simple. Appliquée aux probabilités et aux statistiques, la régression linéaire multiple a pour objectif d’expliciter une variable \(Y\) en fonction de plusieurs variables aléatoires \(X_1,…,X_n\).
En disposant d’un échantillon de ces variables aléatoires \((y_i, x_{i,1},…,x_{i,n})\), on cherche \((a_0,…,a_n)\) tels que \(y_i=a_0+a_1x_{i,1}+…+a_nx_{i,n}\).
Pour cela, on utilise la même méthode que pour la régression linéaire simple en posant les mêmes vecteurs \(X, Y\) et \(U\) et en posant \(A=\begin{pmatrix} 1 & x_{1,1} & \ldots
& x_{1,n} \\ 1 & x_{2,1} & \ldots &
x_{2,p} \\ \vdots &\vdots & & \vdots \\ 1
& x_{n,1} & \ldots & x_{n,p} \end{pmatrix}\)
Remarque
Cette méthode peut paraître longue et fastidieuse, mais c’est toujours la même, il est donc utile de la connaître. Une fois maîtrisée, elle ne pose aucun problème, tant que tu ne te trompes pas dans les systèmes intermédiaires.
La régression linéaire multiple est très rare aux concours. Il peut être intéressant d’en avoir entendu parler, mais ne panique pas, elle n’est pas essentielle pour réussir les mathématiques au concours. L’important est déjà d’avoir compris la méthode de régression linéaire simple.
