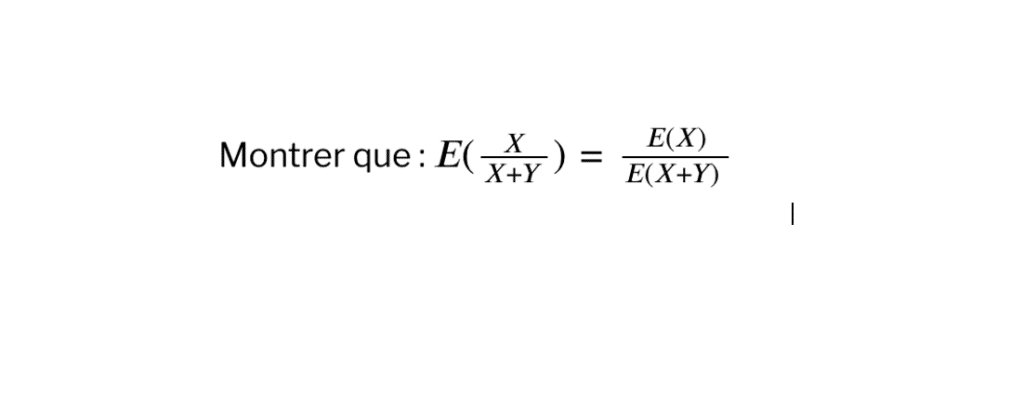On se retrouve pour la résolution d’un exercice d’oral classique type ESCP, qui conviendra aux mathématiques approfondies comme aux mathématiques appliquées. Pour commencer cette série, on s’attaquera à un thème central du programme de mathématiques ECG : les probabilités. Thème roi des sujets de concours (écrits comme oraux), ce court exercice te permettra de manier quelques propriétés fondamentales de l’espérance de variables aléatoires.
Résolution de l’exercice
Soit X et Y deux variables aléatoires indépendantes, positives, de même loi et admettant toutes deux une espérance.
Montrer que : \(E(\frac{X}{X+Y})=\frac{E(X)}{E(X+Y)}\)
On sait que X et Y admettent une espérance, donc X+Y admet une espérance et \(E(X+Y)=E(X)+E(Y)\), d’après la linéarité de l’espérance.
Aussi, comme X et Y sont positives, on sait que \(0\leq \frac{X}{X+Y}\leq 1\), donc \(\frac{X}{X+Y}\) est borné et admet une espérance.
X et Y suivent même loi, donc admettent la même espérance. Ainsi, \(E(X+Y)=E(X)+E(X)\).
D’où, \(E(X+Y)=2E(X)\).
Alors, on a ainsi : \(\frac{E(X)}{E(X+Y)}=\frac{1}{2}\).
Montrons désormais que : \(E(\frac{X}{X+Y})=\frac{1}{2}\).
On sait que X et Y sont de même loi, donc \(\frac{X}{X+Y}\) et \(\frac{Y}{X+Y}\) sont de même loi.
Or, \(\frac{X}{X+Y}+\frac{Y}{X+Y}=1\).
Ainsi, \(E(\frac{X}{X+Y})+E(\frac{Y}{X+Y})=1\) d’après la linéarité de l’espérance.
X et Y suivant même loi, on peut ainsi écrire : \(E(\frac{X}{X+Y})+E(\frac{X}{X+Y})=1\).
Donc, \(2\, E(\frac{X}{X+Y})=1\).
Ainsi, on a bien : \(E(\frac{X}{X+Y})=\frac{1}{2}\).
Finalement, \(E(\frac{X}{X+Y})=\frac{E(X)}{E(X+Y)}\).
N’hésite pas à consulter toutes nos ressources de mathématiques !