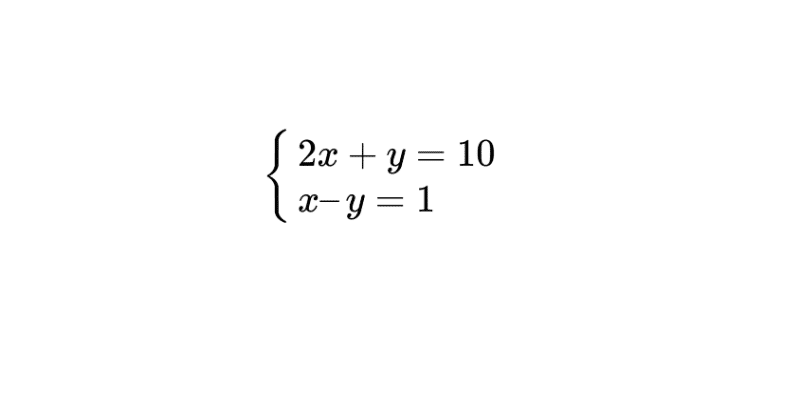Un système d’équations linéaires est un ensemble de deux ou plusieurs équations comportant plusieurs inconnues. L’objectif est de trouver les valeurs de ces inconnues qui satisfont simultanément toutes les équations du système. Ces systèmes peuvent être résolus par différentes méthodes, chacune ayant ses avantages et ses inconvénients en fonction du contexte et du type de système. Major-Prépa est là pour t’aider à y voir plus clair.
Première méthode : la substitution
La méthode de substitution consiste à isoler une inconnue dans l’une des équations, puis à substituer cette expression dans les autres équations.
Cette méthode est particulièrement efficace pour les systèmes simples ou lorsqu’une des équations peut facilement être résolue pour une inconnue.
Exemple
Considérons le système suivant :
\[
\begin{cases}
2x + y = 10 \\
x – y = 1
\end{cases}
\]
Étape 1 : Résolvons la deuxième équation pour \( x \)
\[
x = y + 1
\]
Étape 2 : Substituons \( x = y + 1 \) dans la première équation
\[
2(y + 1) + y = 10
\]
Étape 3 : Résolvons pour \( y \)
\[
2y + 2 + y = 10 \Rightarrow 3y = 8 \Rightarrow y = \frac{8}{3}
\]
Étape 4 : Remplaçons \( y \) dans \( x = y + 1 \)
\[
x = \frac{8}{3} + 1 = \frac{11}{3}
\]
Ainsi, la solution est \[ \fbox{\( \displaystyle x = \frac{11}{3} \) et \( y = \frac{8}{3} \)}\]
Deuxième méthode : la combinaison linéaire
Cette méthode consiste à additionner ou à soustraire les équations du système de manière à éliminer une des inconnues.
Cela permet de se ramener à une équation simple.
Exemple
Considérons le système suivant :
\[
\begin{cases}
3x + 2y = 11 \\
2x – 2y = 2
\end{cases}
\]
Étape 1 : Additionnons les deux équations pour éliminer \( y \)
\[
(3x + 2y) + (2x – 2y) = 11 + 2
\]
\[
5x = 13 \Rightarrow x = \frac{13}{5}
\]
Étape 2 : Remplaçons \( x \) dans la première équation
\[
3\left(\frac{13}{5}\right) + 2y = 11
\]
\[
\frac{39}{5} + 2y = 11 \Rightarrow 2y = 11 – \frac{39}{5} = \frac{16}{5} \Rightarrow y = \frac{8}{5}
\]
Ainsi, la solution est \[ \fbox{\( \displaystyle x = \frac{13}{5} \) et \( y = \frac{8}{5} \)}\]
Troisième méthode : l’inversion de matrice
Les systèmes d’équations linéaires peuvent également être résolus à l’aide des matrices.
Si la matrice des coefficients \( A \) est inversible, la solution du système \( AX = B \) (où \( X \) est le vecteur des inconnues et \( B \) le vecteur des constantes) est donnée par \( X = A^{-1}B \).
Exemple
Utilisons le même système :
\[
A = \begin{pmatrix} 1 & 1 \\ 2 & -3 \end{pmatrix} \quad \text{et} \quad B = \begin{pmatrix} 5 \\ 4 \end{pmatrix}
\]
L’inverse de \( A \) est :
\[
A^{-1} = \frac{1}{\text{det}(A)} \begin{pmatrix} -3 & -1 \\ -2 & 1 \end{pmatrix} = \frac{1}{-5} \begin{pmatrix} -3 & -1 \\ -2 & 1 \end{pmatrix} = \begin{pmatrix} \frac{3}{5} & \frac{1}{5} \\ \frac{2}{5} & \frac{-1}{5} \end{pmatrix}
\]
Donc, la solution est :
\[
X = A^{-1}B = \begin{pmatrix} \frac{3}{5} & \frac{1}{5} \\ \frac{2}{5} & \frac{-1}{5} \end{pmatrix} \begin{pmatrix} 5 \\ 4 \end{pmatrix} = \begin{pmatrix} \frac{15 + 4}{5} \\ \frac{10 – 4}{5} \end{pmatrix}
\]
\[ \fbox{\( \displaystyle X =\begin{pmatrix} \frac{19}{5} \\ \frac{6}{5} \end{pmatrix} \)} \]
Quatrième méthode : la méthode de Gauss
La méthode de Gauss consiste à transformer le système en un système triangulaire supérieur en utilisant des opérations simples sur les lignes.
Une fois la forme triangulaire atteinte, on peut alors résoudre les équations.
Exemple
Considérons le système suivant :
\[
\begin{cases}
x + y + z = 6 \\
2x + 3y + z = 10 \\
x + 2y + 3z = 13
\end{cases}
\]
Étape 1 : Éliminons \( x \) des deuxième et troisième équations en soustrayant la première équation multipliée par 2 et par 1
\[
\begin{cases}
x + y + z = 6 \\
(2x + 3y + z) – 2(x + y + z) = 10 – 12 \\
(x + 2y + 3z) – (x + y + z) = 13 – 6
\end{cases}
\]
Ce qui donne :
\[
\begin{cases}
x + y + z = 6 \\
y – z = -2 \\
y + 2z = 7
\end{cases}
\]
Étape 2 : Résolvons le système triangulaire en commençant par \( y \) et \( z \)
De la deuxième équation, \( y = z – 2 \).
Substituons dans la troisième équation :
\[
(z – 2) + 2z = 7 \Rightarrow 3z = 9 \Rightarrow z = 3
\]
Puis, \( y = 3 – 2 = 1 \).
Enfin, substituons dans la première équation pour trouver \( x \) :
\[
x + 1 + 3 = 6 \Rightarrow x = 2
\]
Ainsi, la solution est \[ \fbox{\( x = 2 \), \( y = 1 \) et \( z = 3 \)} \]
Cinquième méthode : l’utilisation d’un graphique
La méthode graphique est utilisée pour résoudre des systèmes d’équations linéaires avec deux variables en traçant les droites correspondant aux équations sur un plan cartésien et en trouvant leurs points d’intersection.
Cette technique est simple, mais manque de précison. Il vaut mieux l’utiliser pour vérifier un résultat obtenu à l’aide d’une des méthodes précédentes.
Exemple
Considérons le système suivant :
\[
\begin{cases}
x + y = 5 \\
2x – y = 1
\end{cases}
\]
Étape 1 : Réécrivons les équations sous la forme y = f(x)
On obtient :
\[
\begin{cases}
y = 5 – x \\
y = 2x – 1
\end{cases}
\]
Étape 2 : Traçons les droites
On trouve :
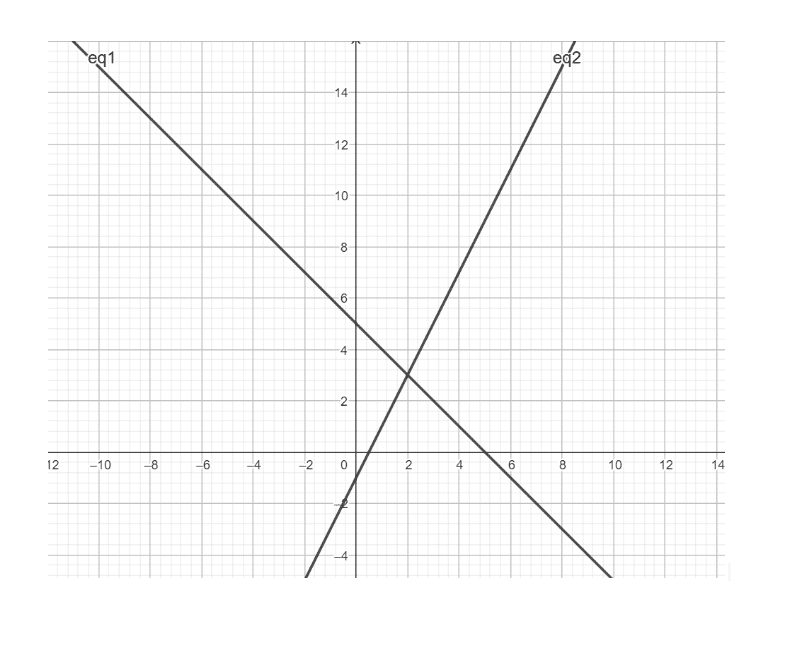
Ainsi, la solution du système est \[ \fbox{\( x = 2 \) et \( y = 3 \)} \]
Exercice
Maintenant que tu connais différentes méthodes classiques pour résoudre un système d’équations, tu peux t’entraîner sur cet exercice.
Questions
1. Résous ce système en utilisant tour à tour les quatre premières méthodes présentées plus haut dans l’article.
\[
\begin{cases}
3x – y + 2z = 7 \\
2x + y – z = 4 \\
x + 3y + z = 10
\end{cases}
\]
2. Résous les systèmes d’équations linéaires suivants en utilisant la méthode qui te semble la plus performante.
\(\begin{cases}
3x + y = 7 \\
2x + y = 5
\end{cases}\)
\(\begin{cases}
x + 2y = 3 \\
2x – y = 1
\end{cases}\)
Solutions
Corrigé de la question 1
a) Résolution par substitution
Pour appliquer la méthode de substitution, nous allons isoler une des variables dans une des équations et la substituer dans les autres.
Étape 1 : Isolons \( z \) dans la première équation
\[
2z = 7 – 3x + y \Rightarrow z = \frac{7 – 3x + y}{2}
\]
Étape 2 : Substituons cette expression pour \( z \) dans les deux autres équations
Pour la deuxième équation :
\[
2x + y – \frac{7 – 3x + y}{2} = 4
\]
Multiplions par 2 pour éliminer le dénominateur :
\[
4x + 2y – (7 – 3x + y) = 8 \Rightarrow 7x + y = 15
\]
Pour la troisième équation :
\[
x + 3y + \frac{7 – 3x + y}{2} = 10
\]
Multiplions par 2 pour éliminer le dénominateur :
\[
2x + 6y + 7 – 3x + y = 20 \Rightarrow -x + 7y = 13
\]
Étape 3 : Résolvons le système des deux équations en \( x \) et \( y \)
\[
\begin{cases}
7x + y = 15 \\
-x + 7y = 13
\end{cases}
\]
Isolons \( y \) dans la première équation :
\[
y = 15 – 7x
\]
Substituons dans la deuxième équation :
\[
-x + 7(15 – 7x) = 13 \Rightarrow -x + 105 – 49x = 13 \Rightarrow -50x = -92 \Rightarrow x = \frac{46}{25}
\]
Substituons dans \( y = 15 – 7x \) :
\[
y = 15 – 7 \times \frac{46}{25} = \frac{43}{25}
\]
Enfin, substituons dans \( z = \frac{7 – 3x + y}{2} \) pour trouver \( z \) :
\[
z = \frac{7 – 3 \times \frac{46}{25} + \frac{43}{25}}{2} = \frac{\frac{48}{25}}{2} = \frac{24}{25}
\]
La solution est donc \[ \fbox{\( \displaystyle
x = \frac{46}{25}, y = \frac{43}{25}, z = \frac{24}{25}
\)}\]
b) Résolution par combinaison linéaire
Étape 1 : Éliminons \( y \) en combinant les équations
Additionnons la deuxième équation à la première pour éliminer \( y \) :
\[
(3x – y + 2z) + (2x + y – z) = 7 + 4 \Rightarrow 5x + z = 11
\]
Maintenant, soustrayons la deuxième équation de la troisième :
\[
(x + 3y + z) – (2x + y – z) = 10 – 4 \Rightarrow -x + 2y + 2z = 6
\]
Nous avons maintenant un système en \( x \) et \( z \) :
\[
\begin{cases}
5x + z = 11 \\
-x + 2y + 2z = 6
\end{cases}
\]
Étape 2 : Isolons \( z \) dans la première équation
\[
z = 11 – 5x
\]
Substituons dans la deuxième équation :
\[
-x + 2y + 2(11 – 5x) = 6 \Rightarrow -11x + 2y = -16 \Rightarrow 2y = 11x – 16
\]
Isolons \( y \) :
\[
y = \frac{11x – 16}{2}
\]
Substituons dans la troisième équation :
\[
x + 3 \times \frac{11x – 16}{2} + 11 – 5x = 10
\]
Simplifions pour obtenir :
\[
11x + 7y = 43
\]
La solution complète est :
\[ \fbox{\( \displaystyle
x = \frac{46}{25}, \; y = \frac{43}{25}, \; z = \frac{24}{25}
\)}\]
c) Résolution par inversion des matrices
Nous représentons le système sous forme matricielle \( AX = B \) :
\[
A = \begin{pmatrix} 3 & -1 & 2 \\ 2 & 1 & -1 \\ 1 & 3 & 1 \end{pmatrix}, \quad X = \begin{pmatrix} x \\ y \\ z \end{pmatrix}, \quad B = \begin{pmatrix} 7 \\ 4 \\ 10 \end{pmatrix}
\]
Calculons l’inverse de la matrice \( A \), puis trouvons \( X = A^{-1}B \).
Inverse :
\[
A^{-1}B = \begin{pmatrix} 1 & 2 & 1 \end{pmatrix} = \frac{1}{\det(A)} \left(\sum(A)\right)
\]
En calculant \( X = A^{-1}B \), nous retrouvons la solution
\[ \fbox{\( \displaystyle
x = \frac{46}{25}, y = \frac{43}{25}, z = \frac{24}{25}
\)}\]
d) Résolution par la méthode de Gauss
Étape 1 : Utilisons des opérations élémentaires pour transformer le système en une forme triangulaire
\[
\begin{cases}
x + 2y + z = 7 \\
x + 3y + z = 10
\end{cases}
\]
Étape 2 : Résolvons pour \( x, y, z \)
On trouve donc \[ \fbox{\( \displaystyle
x = \frac{46}{25}, y = \frac{43}{25}, z = \frac{24}{25}
\)}\]
Corrigé de la question 2
a) Premier système
La méthode de soustraction directe est évidente ici, car les équations ont des termes similaires qui s’annulent facilement.
Soustrayons la deuxième équation de la première :
\[
(3x + y) – (2x + y) = 7 – 5
\]
\[
x = 2
\]
Substituons \( x = 2 \) dans la deuxième équation pour trouver \( y \) :
\[
2(2) + y = 5 \Rightarrow y = 1
\]
Ainsi, la solution est \[\fbox{(x, y) = (2, 1)}\]
b) Deuxième système
Avec deux équations simples, la substitution est la méthode la plus directe.
Isolons \( x \) dans la première équation :
\[
x = 3 – 2y
\]
Substituons dans la deuxième équation :
\[
2(3 – 2y) – y = 1 \Rightarrow 6 – 4y – y = 1 \Rightarrow -5y = -5 \Rightarrow y = 1
\]
Remplaçons \( y = 1 \) dans l’expression de \( x \) :
\[
x = 3 – 2(1) = 1
\]
Ainsi, la solution est \(\fbox{(x, y) = (1, 1)}\)
N’hésite pas à faire et à refaire des exercices de résolutions simples pour ensuite te tester sur des problèmes plus compliqués.
Tu peux consulter nos articles sur les équations différentielles :
- Six astuces sur les équations différentielles
- Liens entre équations différentielles et systèmes différentiels
Tu peux également approfondir ta maîtrise de cette notion grâce à ces articles :
- Résolution de l’équation différentielle logistique (hors programme ECG)
- Les équations différentielles à coefficients non constants (hors programme ECG)
Tu peux retrouver ici le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder ici à toutes nos autres ressources mathématiques !