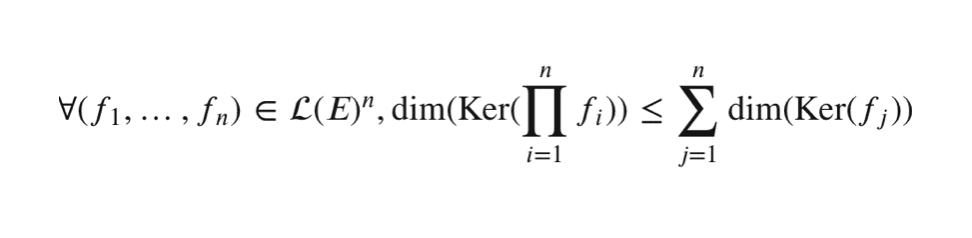Salut à toi, jeune 2A ! Tu es à la recherche de résultats hors programme par simple curiosité ou pour briller le jour des concours ? Alors, tu as ouvert le bon article. Aujourd’hui, nous allons démontrer un (deux ?!) résultat(s) hors programme pouvant s’avérer bien utile, tant à l’écrit qu’à l’oral. C’est parti !
Énoncé
Nous allons commencer par rappeler que le programme d’ECG se restreint désormais à \(\mathbb{R}\). C’est pourquoi nous adopterons le symbole \(\mathbb{R}\).
Soit \( n \in \mathbb{N}^*\). Soit \(E\) un \(\mathbb{K}\)-espace vectoriel de dimension \( n\).
(\(f \) diagonalisable) \(\Leftrightarrow\) ( il existe un polynôme \(P \in \mathbb{K}[X]\), non nul, scindé et à racines simples, qui annule \(f\)).
Démonstration
\( \fbox{\(\Rightarrow\)}\) Supposons que \(f\) soit diagonalisable et prouvons l’existence d’un tel polynôme
Notons \(\lambda_1,…,\lambda_p\) les \(p\) valeurs propres distinctes de \(f\) avec \(p\in[\![1,n]\!]\). Et notons \( E_{\lambda_i}(f)\) les sous-espaces propres de \(f\) rattachés aux \(\lambda_i\) avec \(i\in[\![1,n]\!]\).
On note aussi \(P(f)=\displaystyle \prod_{k=1}^{p} (f-\lambda_k id)\). Et nous souhaitons montrer que : \(P(f)=\displaystyle \prod_{k=1}^{p} (f-\lambda_k id)=0_{\mathcal{L}(E)}\).
Comme \(f\) est diagonalisable, la CNS de diagonalisabilité nous permet d’écrire : \( E=\displaystyle \bigoplus_{i=1}^{p} E_{\lambda_i}(f)\).
Il vient que :
\( \forall x \in E, \exists! (x_1,…,x_p)\in \displaystyle \prod_{k=1}^{p}E_{\lambda_k}(f): x=\displaystyle \sum_{i=1}^{p}x_i\). Soit un tel \( x\) ainsi décomposé.
\( P(f)(x) = \displaystyle \prod_{k=1}^{p} (f-\lambda_k id)( \displaystyle \sum_{i=1}^{p}x_i)\) \( = \displaystyle \sum_{i=1}^{p} ( \displaystyle \prod_{k=1 k\ne i}^{p} (f-\lambda_k id) \circ (f-\lambda_i id)(x_i)) = 0_{\mathcal{L}(E)}\).
On peut en effet passer de la première à la deuxième égalité en relevant le fait que les \( (f-\lambda_i id)_{i \in [\![1,n]\!]}\) commutent.
Ceci étant vrai pour tout \( x \in E \), on peut conclure : \( P(f) = 0_{\mathcal{L}(E)}\).
Nous venons de prouver l’existence d’un polynôme \(P \in \mathbb{K}[X] \) non nul, scindé et à racines simples annulateur de \( f\).
\( \fbox{\(\Leftarrow\)}\) Supposons \(P \in \mathbb{K}[X] \) non nul, scindé et à racines simples tel que \( P(f) = 0_{\mathcal{L}(E)}\)
On note \(P(x)=\displaystyle \prod_{k=1}^{d} (x-\alpha_k)\), avec \( d\in \mathbb{N} \)*. On veut montrer que \( f\) est diagonalisable, ce qui par la CNS de diagonalisabilité revient à montrer que \( \dim(E) = \displaystyle \sum_{\lambda \in Sp(f)}\dim(E_{\lambda})(f) \).
On a : \(P(f)=\displaystyle \prod_{k=1}^{d} (f-\lambda_k id)=0_{\mathcal{L}(E)}\)
Soit \(i\in[\![1,d]\!]\).
- Si \( \alpha_i \in Sp(f) \), alors on note \( \lambda_i = \alpha_i \)
- Si \( \alpha_i \notin Sp(f) \), alors \( (f-\alpha_i id)^{-1} \) existe et donc on réalise l’opération suivante : \(\displaystyle \prod_{k=1}^{d} (f-\lambda_k id) \circ (f-\alpha_i id)^{-1} = 0_{\mathcal{L}(E)} \circ (f-\alpha_i id)^{-1} = 0_{\mathcal{L}(E)} \)
Quitte à réindexer nos \( \lambda_i \), nous obtenons : \( \displaystyle \prod_{k=1}^{p} (f-\lambda_k id)=0_{\mathcal{L}(E)}\) ( \( p \in [\![1,n]\!] \)) avec \( \lambda_1,…, \lambda_p \in Sp(f) \).
Déjà \( \displaystyle \bigoplus_{i=1}^{p} E_{\lambda_i}(f) \subset E \Rightarrow \displaystyle \sum _{j=1}^p \dim(E_{\lambda_i}(f)) \le n \).
Puis, comme \( \forall x \in E, \displaystyle \prod_{k=1}^{p} (f-\lambda_k id)(x)=0\), en notant \(g=\displaystyle \prod_{k=1}^{p} (f-\lambda_k id) \), on a \( \text{Ker}(g) = E \). Or, on peut montrer que : \(\dim (\text{Ker}(\displaystyle \prod_{k=1}^{p} (f-\lambda_k id)) \le \displaystyle \sum_{i=1}^p \dim(\text{Ker}(f-\lambda_i id)) (*) \).
D’où : \( n =\dim(E) \le \displaystyle \sum_{i=1}^p \dim(\text{Ker}(f-\lambda_i id) \) et donc \( \dim(E) = \displaystyle \sum_{\lambda \in Sp(f)}\dim(E_{\lambda})(f) \).
Par ce que nous avions annoncé, \( f\) est bien diagonalisable, ce qui achève la preuve.
Passons à la démonstration de (*)
Commençons par prouver que : \( \forall (u,v) \in \mathcal{L}(E)^2, \dim(\text{Ker}(u\circ v)) \le \dim(\text{Ker}(u))+ \dim(\text{Ker}(v)) \)}
Soient \( u\) et \( v\) deux endomorphismes de \(E\). Montrons que : \( \dim (\text{Ker}(u \circ v)) \le dim(\text{Ker}(u)) + dim(\text{Ker}(v)) \).
Notons \( f= u_{|\text{Im}(v)} \).
Le théorème du rang nous permet d’écrire : \( \text{rg}(v) = \text{rg}(f) + \dim(\text{Ker}(f)) (1) \).
- \( \text{Im}(f)\) = {\( y \in \text{Im}(f)) : \exists x \in \text{Im}(v), y= f(x)\)} =
{\(y \in \text{Im}(u)) : \exists x \in \text{Im}(v), \exists a \in E, v(a) = x, y= u\circ v (a) \)} = \(\text{Im}(u\circ v) \) - \( \text{Ker}(f)\) = {\( x \in E : f(x)=0\)} \( \subset\) {\(x\in E : u(x)=0\)} =\( \text{Ker}(u)\)
En remplaçant dans \( (1)\) : \( \dim(\text{Im}(v)) – \dim(\text{Ker}(f)) = \dim(\text{Im}(u\circ v)) \\ \)
Puis : \( \dim(E) – \dim( \text{Ker}(v)) – \dim( \text{Ker}(f)) = \dim(E) – \dim( \text{Ker}(u\circ v)) \)
Ou encore : \( \dim(\text{Ker}(u\circ v) = \dim(\text{Ker}(f) + \dim(\text{Ker}(v) \))
or, \( \text{Ker}(f) \subset \text{Ker}(u) \Rightarrow \dim( \text{Ker}(f)) \le \dim( \text{Ker}(u)) \)
On a alors montré que : \( \fbox{ \( \dim(\text{Ker}(u\circ v)) \le \dim(\text{Ker}(u))+ \dim(\text{Ker}(v)) \)} \)
On peut dès lors généraliser en démontrant par récurrence sur \(n \in \mathbb{N}^*\) la proposition qui suit
\( \mathcal{P}(n)\) : \( “\forall (f_1,…,f_n) \in \mathcal{L}(E)^n , \dim(\text{Ker}(\displaystyle \prod_{i=1}^n f_i)) \le \displaystyle \sum_{j=1}^n \dim(\text{Ker}(f_j)) ” \ \)
Initialisation : Soit \( f \in \mathcal{L}(E) \). Il est clair que \( \dim(\text{ker}(f) \le \dim(\text{ker}(f) \)).
Hérédité : Soit \( n \in \mathbb{N} \)* tel que la proposition \( \mathcal{P}(n)\) soit vraie. Soit \( (f_1,…,f_{n+1}) \in \mathcal{L}(E)^{n+1}\).
Comme \( \displaystyle \prod_{i=1}^n f_i \in \mathcal{L}(E) \) et \( f_{n+1} \in \mathcal{L}(E) \), nous pouvons appliquer le résultat démontré ci-dessus en prenant : \( u=\displaystyle \prod_{i=1}^n f_i \) et \( v=f_{n+1} \).
C’est-à-dire : \( \dim(\text{Ker}( \displaystyle \prod_{i=1}^n f_i) \circ f_{n+1}) \le \dim(\text{Ker}( \displaystyle \prod_{i=1}^n f_i)) + \dim(\text{Ker}(f_{n+1}) \)).
Puis, par l’hypothèse de récurrence : \( \dim(\text{Ker}( \displaystyle \prod_{i=1}^{n+1} f_i)) \le \sum_{j=1}^{n+1} \dim(\text{Ker}(f_j)) \). Ce qui achève l’hérédité et notre récurrence.
Voilà, cet article portant sur un (voire deux) exercice(s) très classique(s) hors programme touche à sa fin, j’espère qu’il t’aura été utile. À bientôt !
N’hésite pas à consulter toutes nos ressources de mathématiques !