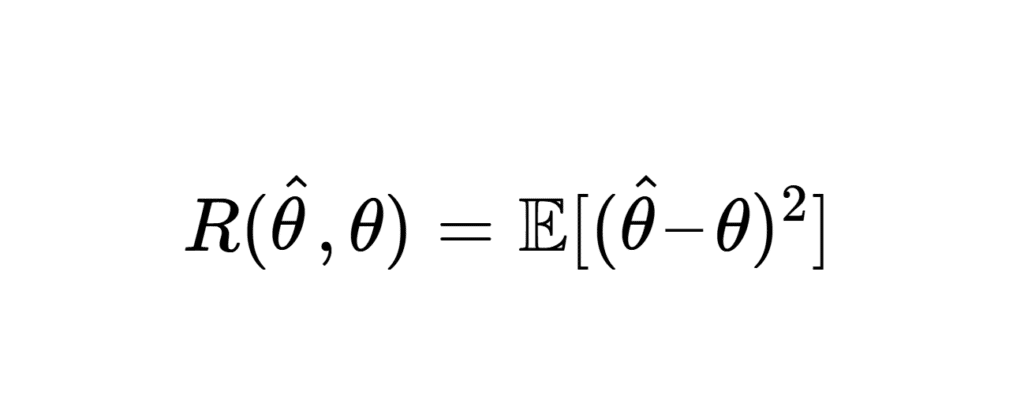Le risque quadratique est une notion centrale en théorie de l’estimation statistique. Cette notion était au programme avant la réforme des prépas EC et ne l’est plus désormais. Mais elle tombe encore souvent aux concours, notamment dans les sujets de Parisiennes. Il est donc toujours bon d’être à l’aise avec cette notion pour gagner en fluidité le jour J.
Introduction à la notion
Ton professeur a sûrement dû l’évoquer, un estimateur cherche à estimer un paramètre inconnu (que nous noterons ici \(\theta \in \mathbb{R}\)). L’objectif est de l’estimer à partir d’un échantillon \(\mathbf{X} = (X_1, X_2, \dots, X_n)\). Seulement, rien n’assure que cette estimation du paramètre soit parfaite.
Pour étudier cette perfectibilité de l’estimateur, il est bon de connaître « l’écart » entre l’estimateur et le paramètre estimé, afin de connaître la « précision de cet estimateur ». Et c’est précisément la notion de risque quadratique qui nous permet de faire cela.
Définition
Soit \(\theta \in \mathbb{R}\) un paramètre inconnu que l’on cherche à estimer à partir de données \(\mathbf{X} = (X_1, X_2, \dots, X_n)\). Prenons un estimateur \(\hat{\theta}\) qui admet un moment d’ordre 2.
Pour définir le risque quadratique, nous avons donc besoin d’un estimateur d’un paramètre inconnu que l’on cherche à estimer, ainsi qu’un échantillon donné. À partir de là, le risque quadratique de \(\hat{\theta}\) est défini comme :
\[ R(\hat{\theta}, \theta) = \mathbb{E}[(\hat{\theta} – \theta)^2] \]
où l’espérance est prise par rapport à la loi de \(\mathbf{X}\)
Le risque quadratique combine deux termes fondamentaux :
\[ R(\hat{\theta}, \theta) = \mathrm{Var}(\hat{\theta}) + \text{Biais}^2(\hat{\theta}, \theta), \] avec :
\[ \text{Biais}(\hat{\theta}, \theta) = \mathbb{E}[\hat{\theta}] – \theta \]
Propriétés
Non-négativité
\(R(\hat{\theta}, \theta) \geq 0\).
Cette propriété découle de la définition comme une espérance d’une quantité positive \((\hat{\theta} – \theta)^2\). Comme tu le sais déjà, la propriété de positivité de l’espérance assure que cette quantité est positive, c’est-à-dire que le risque quadratique est toujours positif.
Décomposition biais-variance
\[ R(\hat{\theta}, \theta) = \mathrm{Var}(\hat{\theta}) + (\mathbb{E}[\hat{\theta}] – \theta)^2. \]
Cela met en lumière le compromis entre le biais et la variance dans la conception des estimateurs. La démonstration est plutôt facile, il suffit de repartir de la définition du risque quadratique, de développer l’identité remarquable et d’utiliser la propriété de linéarité de l’espérance. Ensuite, tu peux repartir de \(\mathrm{Var}(\hat{\theta}) + (\mathbb{E}[\hat{\theta}] – \theta)^2 \) et décomposer ceci de la même manière (spoiler : tu trouveras les deux mêmes expressions).
Linéarité
Posons un autre estimateur \(\hat{\theta} \), transformation linéaire d’un autre estimateur \(\hat{\theta}_1 \). Nous pouvons alors chercher si le risque quadratique est linéaire. \(\hat{\theta} = a\hat{\theta}_1 + b\), alors :
\[ R(a\hat{\theta}_1 + b, \theta) = a^2 R(\hat{\theta}_1, \theta) + (b – \theta)^2. \]
Il apparaît donc que le risque quadratique n’est pas linéaire, mais que l’on peut toutefois exprimer relativement facilement la quantité \( R(a\hat{\theta}_1 + b, \theta) \)
Risque minimum
Comme nous l’avons déjà vu dans l’introduction de cet article, ce qui est intéressant avec les estimateurs, c’est d’avoir un risque minimum pour bien approcher le paramètre étudier. L’objectif est donc de trouver un estimateur dont le risque quadratique est minimal.
L’estimateur \(\hat{\theta}\) qui minimise le risque quadratique est souvent appelé estimateur de Bayes, ou encore estimateur à biais nul lorsque \(\mathbb{E}[\hat{\theta}] = \theta\).
Convergence de l’estimateur et risque quadratique
\[
\left( \lim \limits_{n \to +\infty} \mathbb{E}(\hat{\theta}_n) = \theta \quad \text{et} \quad \lim \limits_{n \to +\infty} \mathrm{Var}(\hat{\theta}_n) = 0 \right)
\iff \lim \limits_{n \to +\infty} \mathrm{R}(\hat{\theta}_n) = 0 => \hat{\theta}_n \overset{p}{\to} \theta
\]
Démontrons rapidement cette propriété
Par définition, l’erreur quadratique moyenne \(\hat{\theta}\) est donnée par : \( \mathrm{R}(\hat{\theta}) = \mathbb{E}\left[(\hat{\theta} – \theta)^2\right] = \mathrm{Var}(\hat{\theta}) + \left( \mathbb{E}[\hat{\theta}] – \theta \right)^2. \)
Ensuite, pour que \(\lim \limits_{n \to +\infty} \mathrm{R}(\hat{\theta}) = 0\), les deux termes \(\mathrm{Var}(\hat{\theta})\) et \(\left( \mathbb{E}[\hat{\theta}] – \theta \right)^2\) doivent tendre vers \(0\) lorsque \(n \to \infty\).
Cela implique : \( \lim \limits_{n \to +\infty} \mathrm{Var}(\hat{\theta}) = 0 \quad \text{et} \quad \lim \limits_{n \to +\infty} \mathbb{E}[\hat{\theta}] = \theta. \)
Par définition, un estimateur \(\hat{\theta}\) converge en probabilité vers \(\theta\) (noté \(\hat{\theta} \overset{p}{\to} \theta\)) si, pour tout \(\epsilon > 0\), on a :
\( \lim \limits_{n \to +\infty} \mathbb{P}(|\hat{\theta} – \theta| > \epsilon) = 0. \)
En utilisant la définition de la variance et du biais, on peut écrire : \(\displaystyle \mathbb{P}(|\hat{\theta} – \theta| > \epsilon) \leq \frac{\mathrm{R}(\hat{\theta})}{\epsilon^2}, \) par l’inégalité de Bienaymé-Tchebychev.
Si \(\lim \limits_{n \to +\infty} \mathrm{R}(\hat{\theta}) = 0\), alors \(\mathbb{P}(|\hat{\theta} – \theta| > \epsilon) \to 0\), ce qui implique \(\hat{\theta} \overset{p}{\to} \theta\).
De plus, la condition \(\lim \limits_{n \to +\infty} \mathrm{R}(\hat{\theta}) = 0\) est équivalente à : \( \lim \limits_{n \to +\infty} \mathbb{E}[\hat{\theta}] = \theta \quad \text{et} \quad \lim \limits_{n \to +\infty} \mathrm{Var}(\hat{\theta}) = 0, \) ce qui achève la démonstration.
Comparaison d’estimateurs
Le risque quadratique permet la comparaison d’estimateurs à partir de leur risque quadratique. Il apparaît clairement par la définition d’un estimateur que l’on préférera celui dont le risque quadratique est le plus faible.
Ce moyen de comparaison est toutefois trop pauvre, le meilleur estimateur en \(theta\) est toujours \(theta\) (trivial, mais cela ne sert à rien de dire cela : on ne prend pas un estimateur égal à la quantité que l’on cherche à approcher).
Un exemple classique
Estimateur de la moyenne
Soit \(\mathbf{X} = (X_1, X_2, \dots, X_n)\) un échantillon i.i.d. de taille \(n\) d’une variable aléatoire \(X \sim \mathcal{N}(\mu, \sigma^2)\). L’estimateur \(\displaystyle \hat{\mu} = \frac{1}{n} \sum_{i=1}^n X_i\) est un estimateur sans biais de \(\mu\).
On trouve par un calcul assez rapide en utilisant la linéarité de l’espérance et les propriétés de la variance sur une suite de variables aléatoires indépendantes que : \(\mathbb{E}[\hat{\mu}] – \mu = 0\) et \(\displaystyle \mathrm{Var}(\hat{\mu}) = \frac{\sigma^2}{n}\)
Le risque quadratique est donc : \[ R(\hat{\mu}, \mu) = \mathrm{Var}(\hat{\mu}) = \displaystyle \frac{\sigma^2}{n}. \]
Et Python dans tout ça
Voici un code Python permettant d’illustrer la notion de risque quadratique comme erreur d’estimation à partir d’une suite d’estimateurs cherchant à estimer le paramètre constant égal à 3.
Et voici ce que renvoie ce code, illustrant de fait que les réalisations des variables aléatoires se dispersent autour de la valeur à estimer. Autrement dit, l’estimateur n’est pas égal à la valeur qu’il cherche à estimer : 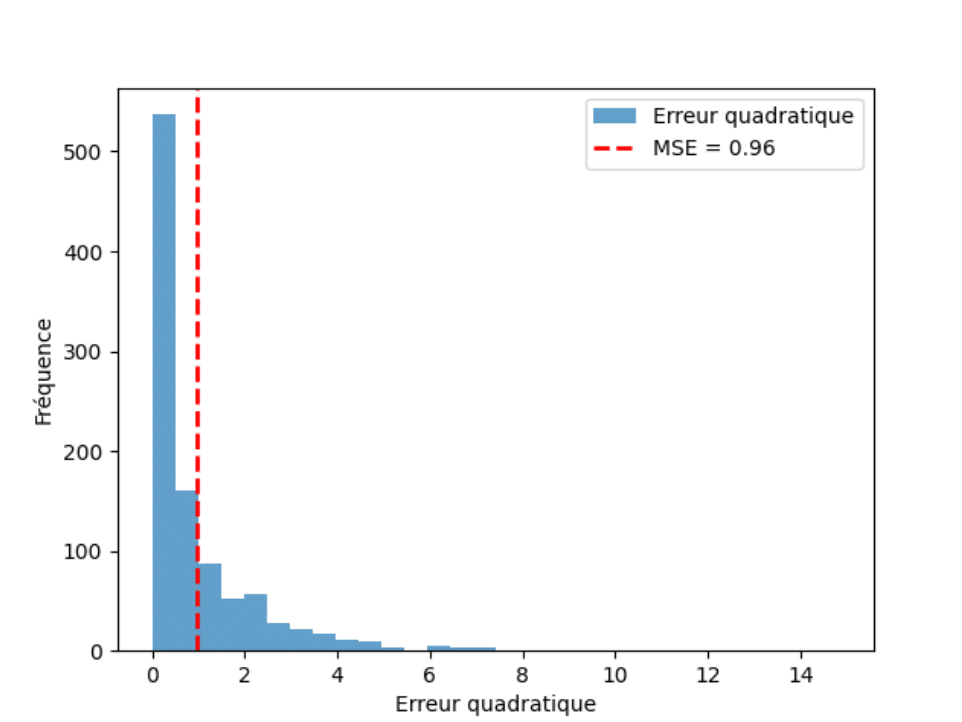
Conclusion
La notion de risque quadratique est centrale dans le cours sur les estimateurs. Elle est au fondement de ces derniers, car elle permet justement d’apprécier la « qualité » de l’estimateur.
Si cette notion n’est plus explicitement au programme, elle continue de tomber dans les sujets de Maths I et de Maths II. L’objectif n’est pas forcément de connaître par cœur ces propriétés, mais de pouvoir avoir une certaine aisance avec ces dernières. Cela te donnera déjà un sérieux avantage le jour des concours.
Il n’y a désormais plus qu’à espérer que cette notion tombe le jour J aux concours !
Tu peux retrouver le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder à toutes nos autres ressources mathématiques !