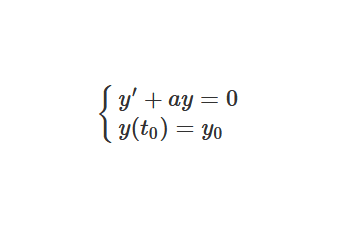Le nouveau programme d’ECG maths appliquées, qui vient remplacer les maths vues en ECE auparavant, offre la possibilité d’étudier les équations différentielles. Ces dernières prennent pour inconnues des fonctions et n’ont donc pas du tout les mêmes propriétés que des équations classiques. Je te propose ici six astuces visant à t’aider dans la résolution de ces équations. Je vais ici de proposer quelques « schémas classiques » concernant des équations différentielles reconnaissables.
Cet article s’adresse uniquement aux maths appliquées, mais peut constituer des notions hors programme pour les maths approfondies.
Les équations différentielles au second membre nul
Certaines équations différentielles (ou certains morceaux d’équations différentielles) peuvent être très facilement résolues lorsque l’on connaît certaines caractéristiques des fonctions dérivées.
Premièrement
Soit \( I \) un intervalle de \( \mathbb{R} \).
Soit \( f \) une fonction de la variable réelle à valeurs réelles dérivable sur \( I \).
Alors, on a l’équivalence :
\( \begin{align*}
\text{(i)} \quad &\forall x \in I, f'(x) = 0. \\
\text{(ii)} \quad &f \text{ est constante sur } I \quad (\text{autrement dit : } \exists C \in \mathbb{R}, \forall x \in I, f(x) = C).
\end{align*} \)
Deuxièmement
Soit \( f \) une fonction de la variable réelle à valeurs réelles dérivable deux fois sur \( I \).
Alors, on a l’équivalence :
\( \begin{align*}
\text{(i)} \quad &\forall x \in I, f^{\prime \prime}(x) = 0. \\
\text{(ii)} \quad &f \text{ est affine sur } I \quad (\text{autrement dit : } \exists (a, b) \in \mathbb{R}^2, \forall x \in I, f(x) = ax + b).
\end{align*} \)
Plus généralement
Soit \( n \in \mathbb{N}^* \).
Soit \( f \) une fonction de la variable réelle à valeurs réelles dérivable \( n \) fois sur \( I \).
Alors, on a l’équivalence :
\( \begin{align*}
\text{(i)} \quad &\forall x \in I, f^{(n)}(x) = 0. \\
\text{(ii)} \quad &f \text{ est de la forme suivante : } \ \exists (a_0, a_1, \ldots, a_{n-1}) \in \mathbb{R}^n, \forall x \in I, f(x) = \sum_{k=0}^{n-1} a_k \times x^{k}.
\end{align*} \)
Ainsi, quand tu as une équation différentielle dans laquelle apparaît une fonction égale à 0, tu peux te référer à ce formulaire pour aller plus vite dans la résolution. Je te laisse faire les démonstrations de ces équivalences pour t’entraîner.
Les équations différentielles au second membre constant
On s’intéresse ici au fait de trouver une solution particulière à une équation différentielle ayant un second membre constant. Celles-ci peuvent être trouvées sans calcul.
Au premier degré
Soit \( I \) un intervalle de \( \mathbb{R} \).
On notera pour la suite \( \mathcal{A}(I, \mathbb{R}) \) l’ensemble des applications de \(I\) dans \(R\).
On prend deux réels \( a \) et \( b \) (Attention : b est un réel !) tels que :
\[ (E) : y’ + ay = b, \text{d’inconnue} \ y \in \mathcal{A}(I, \mathbb{R}) \]
On suppose que \( a \ne 0 \).
Alors, la fonction \( H : \begin{cases} I \to \mathbb{R} \\t \mapsto \frac{b}{a} \end{cases} \) est une solution de \( (E) \).
Au second degré
Soit \( I \) un intervalle de \( \mathbb{R} \).
On prend trois réels \( a \), \( b \) et \( c \) tels que :
\[ (E) : y^{\prime \prime} + ay’ + by = c, \quad \text{d’inconnue } y \in \mathcal{A}(I, \mathbb{R}). \]
On suppose que \( b \ne 0 \).
Alors, la fonction \( H : \begin{cases} I \to \mathbb{R} \\ t \mapsto \frac{c}{b} \end{cases} \) est une solution de \( (E) \).
Les équations différentielles au second membre polynomial
En règle générale, tu peux aisément te dire que lorsque le second membre de ton équation différentielle est polynomial, tu te dois de chercher une solution particulière polynomiale. Tout va se faire au niveau de l’identification des coefficients, qui te donnera la solution exacte.
Ainsi, tu peux « commencer large », en prenant un polynôme de quelques degrés supérieurs à ton second membre. Ceci sera plus long, mais c’est un gage de sûreté, puisque tu peux dès lors être quasi sûr(e) de trouver une solution particulière viable, quitte à trouver quelques coefficients nuls dans ton identification.
Il existe en plus de cela, un cas particulier où je peux te donner directement une solution particulière.
Cas particulier des ED d’ordre deux à second membre polynomial
Soit \( I \) un intervalle.
Soit \( (a, b) \in \mathbb{R}^2 \).
Soit \( P \) une fonction polynomiale.
On prend :
\[(E) : \ y^{\prime \prime} + ay'(t) + by(t) = P(t), \text{d’inconnue } \ y \in \mathcal{A}(I, \mathbb{R}).\]
Trois cas de figure se présentent alors :
\( \begin{align*}
& \text{Cas n°1 : Si } b \neq 0. \\
& \text{Alors, } (E) \text{ possède une solution polynomiale de degré } \deg(P). \\
\\
& \text{Cas n°2 : Si } b = 0 \text{ et } a \neq 0. \\
& \text{Alors, } (E) \text{ possède une solution polynomiale de degré } \deg(P) + 1. \\
\\
& \text{Cas n°3 : Si } b = 0 \text{ et } a = 0. \\
& \text{Alors, } (E) \text{ possède une solution polynomiale de degré } \deg(P) + 2.
\end{align*} \)
Un exemple
**Cas n° 2 : \( b = 0 \) et \( a \neq 0 \)**
Considérons l’équation différentielle suivante :
\[y^{\prime \prime} + 2y’ = t^3 – 1.\]
Dans ce cas, \( b = 0 \), \( a = 2 \) et \( \deg(P) = 3 \) (puisque \( P(t) = t^3 – 1 \)), donc l’équation possède une solution polynomiale de degré \( \deg(P) + 1 = 4 \).
N’oublie pas que pour résoudre ces équations différentielles, il faudrait également faire ton identification pour la solution particulière, résoudre l’équation homogène, puis concaténer les solutions.
Les équations différentielles au second membre
de la forme \( P(t) e^{\alpha t} \)
On rentre ici dans les théorèmes moins évidents (mais qui restent démontrables facilement), qui s’appliquent en l’occurrence ici lorsque le second membre est un produit d’un polynôme par une exponentielle. On peut dès lors trouver la forme d’une solution particulière d’une telle équation.
Au premier degré
Soit \( I \) un intervalle de \( \mathbb{R} \)
Soit \( \alpha \in \mathbb{R} \)
Soit \( a \in \mathbb{R} \)
Soit \( P \) une fonction polynomiale.
On considère l’équation \( \text{(E) :} \ y’ + ay = P(t)e^{\alpha t}, \text{d’inconnue} \ y \in \mathcal{A}(I, \mathbb{R}) \).
Donc :
\( \begin{align*}
\text{1) Si } \ & \alpha \ne -a. \\
& \text{Alors, il existe un polynôme } Q \text{ de degré } \deg(P) \text{ et la fonction } \ t \mapsto Q(t)e^{\alpha t} \text{ est une solution de } (E). \\
\text{2) Si } \ & \alpha = -a. \\
& \text{Alors, il existe un polynôme } Q \text{ de degré } \deg(P) \text{ et la fonction } \ t \mapsto tQ(t)e^{\alpha t} \text{ est une solution de } (E).
\end{align*} \)
Au second degré
On reprend les mêmes notations, avec cette fois-ci \( (a,b) \in \mathbb{R^2}\).
On considère l’équation \( \text{(E)} : \ y^{\prime \prime} + ay’ + by = P(t)e^{\alpha t}, \text{d’inconnue} \ y \in \mathcal{A}(I, \mathbb{R}) \).
On note \((Ec)\) l’équation caractéristique associée à \((E)\).
Alors :
\begin{align*}
\text{1. Si } \ & \alpha \text{ n’est pas solution de } (Ec). \\
& \text{Ici, il existe un polynôme } Q \text{ de degré } \deg(P) \text{ et la fonction } t \mapsto Q(t)e^{\alpha t} \text{ est une solution de } (E). \\
\text{2. Si } \ & \alpha \text{ est solution de } (Ec) \text{ et } (Ec) \text{ possède deux racines distinctes}. \\
& \text{Ici, il existe un polynôme } Q \text{ de degré } \deg(P+1) \text{ et la fonction } t \mapsto Q(t)e^{\alpha t} \text{ est une solution de } (E). \\
\text{3. Si } \ & \alpha \text{ est double solution de } (Ec) \text{ et } (Ec) \text{ possède une racine double}. \\
& \text{Ici, il existe un polynôme } Q \text{ de degré } \deg(P+2) \text{ et la fonction } t \mapsto Q(t)e^{\alpha t} \text{ est une solution de } (E). \\
\end{align*}
Le principe de superposition
Ces cas particuliers peuvent également te servir à résoudre une équation différentielle « en deux fois », avec le principe de superposition. Tu verras que tout ce que je t’ai dit précédemment pourra efficacement se combiner avec le principe de superposition et te permettra d’être beaucoup plus efficace dans tes résolutions. Ce principe est le suivant :
Si le second membre s’écrit sous la forme \( b(x) = b_1(x) + b_2(x) \) : on cherche une solution \( y_1 \) à l’équation \( y'(x) + a(x)y(x) = b_1(x) \) et une solution \( y_2 \) à l’équation \( y'(x) + a(x)y(x) = b_2(x) \)
Alors \( y_1 + y_2 \) est une solution à \( y'(x) + a(x)y(x) = b(x) \).
Le principe de superposition te permet d’aller plus vite sur les équations différentielles qui te sont proposées et est parfois indispensable à la résolution de certaines équations différentielles.
Un exemple
Je te propose de résoudre l’ED \( \text{(E) :} \ y’ – 3y = 7 +8x \times e^{5x}, \ \text{d’inconnue} \ y \ \in A(I, \mathbb{R}) \).
Tu vois qu’il n’est pas aisé de résoudre cette équation de manière « classique ».
On résout d’abord l’ED homogène associée, qui donne une fonction du type \( H : \begin{cases} I \to \mathbb{R} \\ t \mapsto Ke^{3t}, K \in \mathbb{R} \end{cases} \).
On résout ensuite \( \text{(E1) :} \ y’ – 3y = 7 \), qui donne une solution du type \( H1 : \begin{cases} I \to \mathbb{R} \\ t \mapsto -\frac{7}{3} \end{cases} \).
Finalement, on se sert du paragraphe sur les seconds membres du type \(P(t)e^{(\alpha t)} \) pour résoudre l’équation \( \text{(E1) :} y’ – 3y = 8x \times e^{5x} \), en trouvant une solution particulière du type \( H2 : \begin{cases} I \to \mathbb{R} \\ t \mapsto (4x – 2) \times e^{5x} \end{cases} \).
On arrive au final à la solution de l’équation \((E)\) qui est : \( F : \begin{cases} I \to \mathbb{R} \\ t \mapsto Ke^{3t} + (4x – 2) \times e^{5x} -\frac{7}{3}, K \in \mathbb{R} \end{cases} \).
Tu vois donc maintenant comment conjuguer les paragraphes précédents pour arriver à résoudre énormément d’équations différentielles très efficacement. Je te laisse faire les calculs pour t’entraîner si tu le souhaites !
La formule de Cauchy-Lipschitz
On reprend les notations des paragraphes précédents, et on y ajoute \( t_0 \in \mathbb{R} \). Alors :
Soit \((P)\) le problème de Cauchy :
\[ \begin{cases}
y’ + ay = 0, \\
y(t_0) = y_0,
\end{cases}, \text{d’inconnue} \ y \ \in A(I, \mathbb{R}) \]
Alors, \((P)\) possède une unique solution. C’est le principe des problèmes de Cauchy.
Mais je peux ajouter que plus précisément, l’application \( G : \begin{cases} I \to \mathbb{R} \\ t \mapsto y_0e^{-a(t-t_0)} \end{cases} \) est l’unique solution du problème de Cauchy \((P)\).
Ce résultat peut être utile soit pour énoncer directement la solution (s’il s’agit d’une étape intermédiaire dans un exercice lourd), soit pour vérifier ton résultat.
Pour l’ordre deux, il n’existe pas de telle solution générale. Néanmoins, un problème de Cauchy à l’ordre 2 garantit l’existence et l’unicité d’une solution à ce problème.
Exemple
On pose le problème de Cauchy suivant :
\[ \begin{cases}
y’ – 8y = 0, \\
y(3) = 11,
\end{cases}, \text{d’inconnue} \ y \ \in A(I, \mathbb{R}) \]
Tu peux prévoir sans calcul que la seule fonction répondant au problème sera :
\[ f : \begin{cases} I \to \mathbb{R} \\ t \mapsto 11e^{8(t-3)} \end{cases} \]
Conclusion
Te voilà maintenant armé(e) pour aller résoudre des équations différentielles bien plus rapidement et efficacement. Ces différents résultats te permettront de savoir à l’avance ce que tu dois trouver. Ce qui est l’assurance de réussir avant même de débuter ton calcul !
Tu peux retrouver nos autres ressources mathématiques ici.