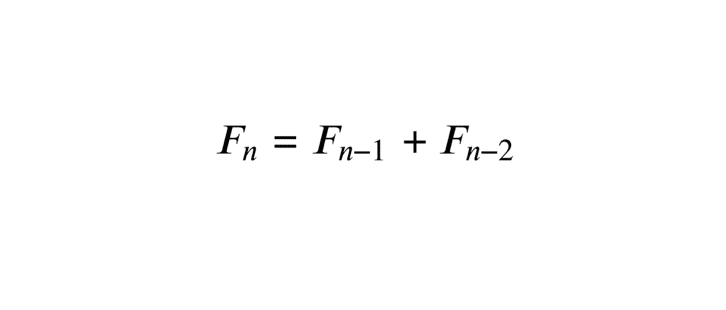La suite de Fibonacci est une série mathématique célèbre (que l’on doit au mathématicien Leonardo Fibonacci) qui commence par les nombres 0 et 1, chaque terme suivant étant la somme des deux termes précédents. Cette suite est particulièrement fascinante en raison de son apparition dans divers contextes, notamment la nature, où elle décrit des motifs tels que la spirale des coquillages et des galaxies. Une explication simple de la suite de Fibonacci implique souvent l’exemple des lapins se reproduisant. De plus, la suite est étroitement liée au nombre d’or, une constante mathématique essentielle pour comprendre les proportions harmonieuses dans l’art et la nature. Cette introduction vise à explorer la méthode de calcul de la suite de Fibonacci et à en démontrer l’utilité et la beauté mathématique. La suite de Fibonacci est une notion hors programme ECG qui est très en vogue ces derniers temps et pourrait faire l’objet d’un sujet de maths aussi bien de province que de parisiennes…
La suite de Fibonacci expliquée en Française
En mathématiques, la suite de Fibonacci est une suite de nombres entiers dans laquelle chaque nombre est la somme des deux nombres qui le précèdent. Elle commence par les nombres 0 et 1, puis se poursuit avec 1 (somme de 0 et 1), 2 (somme de 1 et 1), 3 (somme de 1 et 2), 5 (somme de 2 et 3), 8 (somme de 3 et 5), etc. Les termes de cette suite, c’est-à-dire les nombres apparaissant dans cette suite, sont appelés nombres de Fibonacci.
Définition Formelle de la suite de Fibonacci
La suite de Fibonacci \((F_n)_{n \in \mathbb{N}}\) est définie par : \( F_0 = 0, \) \( F_1 = 1, \) et la relation de récurrence
\[ F_n = F_{n-1} + F_{n-2} \text{ pour } n \geq 2. \]
Les cinq premiers termes de la suite de Fibonacci sont :
1. \( F_0 = 0 \)
2. \( F_1 = 1 \)
3. \( F_2 = 1 \)
4. \( F_3 = 2 \)
5. \( F_4 = 3 \)
La suite de Fibonacci est une suite récurrente linéaire d’ordre 2. Cela signifie que chaque terme est une combinaison linéaire des deux termes précédents, avec des coefficients constants. Cela nous permet d’exprimer \(F_n\) en fonction de \(n\) comme nous le verrons ci-dessous.
A savoir que la suite de Fibonacci se généralise très facilement : les \(k\)-suites de Fibonacci.
La Suite de Fibonacci et le Nombre d’Or
Le Nombre d’Or
Le nombre d’or, souvent noté \(\varphi\), est une constante mathématique irrationnelle qui satisfait l’équation quadratique suivante :
\[ \varphi^2 – \varphi – 1 = 0. \]Les solutions de cette équation sont :
\[ \varphi = \frac{1 + \sqrt{5}}{2} \approx 1.6180339887, \]
et
\[ \varphi’ = \frac{1 – \sqrt{5}}{2} \approx -0.6180339887. \]
Quelques propriétés du nombre d’or incluent :
1. \(\varphi – 1 = \frac{1}{\varphi}\),
2. \(\varphi^2 = \varphi + 1\),
Limite de la suite de Fibonacci et nombre d’or
Il existe un lien remarquable entre la suite de Fibonacci et le nombre d’or. Lorsque \(n\) tend vers l’infini, le rapport de deux termes successifs de la suite de Fibonacci tend vers le nombre d’or :
\[ \lim_{n \to \infty} \frac{F_{n+1}}{F_n} = \varphi. \]
Cette relation met en évidence le lien profond entre la suite de Fibonacci et le nombre d’or, en démontrant que la structure de la suite est intrinsèquement liée à cette constante mathématique fascinante. Cette limite peut se démontrer grâce la formule de Binet.
La Formule de Binet et ses liens avec la suite de Fibonacci
La formule de Binet est une expression explicite pour le \(n\)-ième terme de la suite de Fibonacci. Elle permet de calculer directement un terme de la suite sans avoir besoin de connaître les termes précédents. La formule de Binet est donnée par :
\[ F_n = \frac{\varphi^n – (1 – \varphi)^n}{\sqrt{5}}, \]
où \(\varphi\) est le nombre d’or, soit \(\displaystyle \varphi = \frac{1 + \sqrt{5}}{2}\), et \((1 – \varphi)\) est son conjugué, soit \(\displaystyle \frac{1 – \sqrt{5}}{2}\).
Cette formule découle de la résolution de l’équation caractéristique de la relation de récurrence de la suite de Fibonacci. En effet, puisque \(F_n\) satisfait l’équation de récurrence \(F_n = F_{n-1} + F_{n-2},\) on peut utiliser les racines de l’équation caractéristique associée, \(x^2 – x – 1 = 0\), pour obtenir une solution de la forme :
\[ F_n = A \varphi^n + B (1 – \varphi)^n, \]
où \(A\) et \(B\) sont des constantes déterminées par les conditions initiales de la suite.
En utilisant les valeurs initiales \(F_0 = 0\) et \(F_1 = 1\), on trouve que \(\displaystyle A = \frac{1}{\sqrt{5}}\) et \(\displaystyle B = -\frac{1}{\sqrt{5}}\). Ainsi, la formule de Binet devient :
\[ F_n = \frac{\varphi^n – (1 – \varphi)^n}{\sqrt{5}}. \]
Cette formule est particulièrement utile car elle permet de calculer rapidement des termes élevés de la suite de Fibonacci sans avoir à effectuer tous les calculs intermédiaires, mettant en lumière l’élégance et l’efficacité des méthodes analytiques en mathématiques.
Calcul de la suite de Fibonacci en Python
Pour calculer le \(n\)-ième terme de la suite de Fibonacci en utilisant une boucle “for” en Python, nous pouvons écrire un programme simple qui itère à partir des termes initiaux \(F_0\) et \(F_1\). Voici un exemple de code Python :
Lien avec entre la suite de Fibonacci et la Suite de Lucas
La suite de Lucas est une autre suite définie de manière similaire à la suite de Fibonacci, mais avec des conditions initiales différentes. Elle commence par les nombres 2 et 1, et chaque terme suivant est également la somme des deux termes précédents. Formellement, la suite de Lucas \((L_n)_{n \in \mathbb{N}}\) est définie par : \( L_0 = 2, \) \( L_1 = 1, \)
\[ L_n = L_{n-1} + L_{n-2} \text{ pour } n \geq 2. \]
Les deux suites partagent de nombreuses propriétés et sont souvent étudiées ensemble en raison de leurs similitudes structurelles et de leur lien avec le nombre d’or.
Propriété matricielle de la suite de Fibonacci : les matrices de Fibonacci
L’expression matricielle de la suite de Fibonacci offre une méthode élégante pour représenter et calculer les termes de la suite en utilisant les matrices. À partir de la relation de récurrence \( F_n = F_{n-1} + F_{n-2} \), nous pouvons écrire les matrices de Fibonacci :
\[ \begin{pmatrix}
F_{n+1} \\
F_n
\end{pmatrix}
=
\begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix}
\begin{pmatrix}
F_n \\
F_{n-1}
\end{pmatrix}. \]
En itérant cette relation, nous obtenons une forme matricielle générale :
\[ \begin{pmatrix}
F_n \\
F_{n-1}
\end{pmatrix}
=
\begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix}^n
\begin{pmatrix}
F_1 \\
F_0
\end{pmatrix}. \]
Cela permet d’écrire les termes de la suite de Fibonacci en termes de puissances de matrices. Plus précisément, nous avons :
\[ \begin{pmatrix}
F_{n+1} \\
F_n
\end{pmatrix}
=
\begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix}^n
\begin{pmatrix}
1 \\
0
\end{pmatrix}. \]
Cette formulation matricielle est utile car elle permet d’utiliser des techniques algébriques et numériques pour calculer rapidement les termes de la suite de Fibonacci. Elle met en lumière la structure linéaire de la suite et offre une perspective différente et puissante pour son étude et son calcul.
A noter qu’on retrouve également une notion autour des polynômes de Fibonacci.
Aller plus loin sur la suite de Fibonacci
La suite de Fibonacci est à l’origine de nombreuses recherches et nombreux problèmes mathématiques. Pour y voir plus clair, voici une cartographie de l’ensemble des recherches tournant autour de la suite de Fibonacci (et du nombre d’or) :
| Tableau de correspondances suites/nombres (en lien avec Fibonacci/nombres métalliques) | |
| Suite | Nombre |
| Suite de Fibonacci | Nombre d’or |
| Suite de Pell | Nombre d’argent |
| Généralisation de Fibonacci : les suites k-bonacci | Nombres métalliques : généralisation du nombre d’or |
| Suite de Lucas | Nombre de Lucas |
| Suite de Padovan | Nombre plastique |
| Suite de Perrin | Nombres pseudo-premiers de Perrin |
| Suite de Jacobsthal | Nombres oblongs de Jacobsthal |
| Polynôme/suite de Narayana | Nombre de Narayana |
| Nombre de Gildas | |
| Nombre de Keith | |
| Super nombre d’or | |
Un autre type de généralisation de la suite de Fibonacci est également à découvrir ! Il s’agit de la suite de Fibonacci aléatoire. Elle pourrait clairement faire l’objet d’un sujet de maths parisienne dans les années à venir…
A lire également : le triangle de Pascal (et ses liens avec la suite de Fibonacci).
Conclusion
La suite de Fibonacci révèle une richesse mathématique impressionnante, avec des liens profonds avec le nombre d’or, une constante irrationnelle célèbre pour ses propriétés esthétiques et naturelles. Grâce à la formule de Binet, nous pouvons calculer efficacement les termes de la suite, démontrant l’élégance des méthodes analytiques en mathématiques. L’expression matricielle nous a offert une autre perspective puissante pour comprendre et manipuler cette suite.
L’omniprésence de la suite de Fibonacci dans la nature, des spirales des coquillages aux galaxies, met en lumière l’importance de ces concepts mathématiques. En maîtrisant ces méthodes et relations, nous pouvons mieux apprécier la beauté et l’utilité des mathématiques dans le monde qui nous entoure.
Ainsi, bien que cette notion soit hors programme, la compréhension approfondie de cette dernière te permettra d’améliorer des compétences en analyse et en algèbre linéaire te préparant donc pour les épreuves écrites et orales. Pour t’entraîner sur cette notion, tu peux réaliser les sujets suivants :
- Ecricome 2018 (mathématiques approfondies),
- Maths 1 HEC 2009 (mathématiques appliquées),
- la première Question Sans Préparation des Oraux HEC 2023.
Tu peux retrouver le méga répertoire qui contient toutes les annales de concours et leur corrigé ! Tu peux également accéder à toutes nos autres ressources mathématiques !