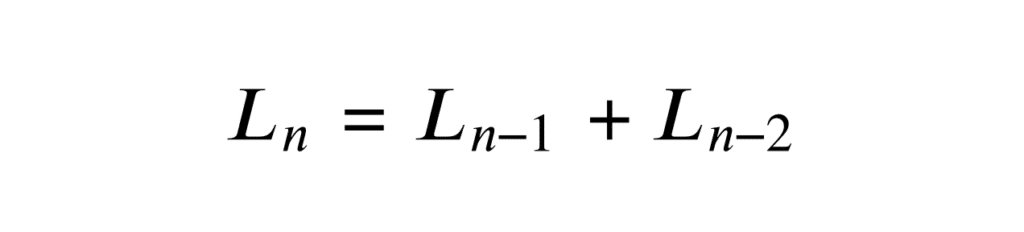La suite de Lucas, du nom du mathématicien français Édouard Lucas qui l’a étudiée à la fin du XIXe siècle, est une séquence de nombres entiers souvent abordée dans des exercices ou des sujets de concours. Bien qu’elle partage des propriétés similaires avec la célèbre suite de Fibonacci, la suite de Lucas présente des caractéristiques uniques qui en font un sujet d’étude fascinant et riche en applications mathématiques. Cette notion est hors programme, cependant une compréhension approfondie de cette dernière te permettra de maîtriser différentes notions importantes et de te préparer au mieux pour les épreuves parisiennes ainsi que pour les oraux de mathématiques !
Définition de la suite par récurrence
La suite de Lucas \((L_n)_{n \in \mathbb{N}}\) est définie de façon récursive comme suit :
\[ \forall n \ge 2, \; L_{n} = L_{n-1} + L_{n-2}\]
avec les conditions initiales \(L_{0} = 2\) et \(L_{1} = 1\).
Cette définition implique que chaque terme de la suite est la somme des deux termes qui le précèdent, commençant par 2 et 1.
Rappel : la suite de Fibonacci diffère légèrement de cette suite, car chacun de ses termes est la somme des deux qui le précèdent, mais les deux premières valeurs sont 0 et 1.
Les premiers termes de la suite
Pour mieux comprendre la suite de Lucas, examinons ses premiers termes :
\[L_{0} = 2, L_{1} = 1, L_{2} = 3, L_{3} = 4, L_{4} = 7, L_{5} = 11, L_{6} = 18 \ldots\]
Comme nous pouvons le voir, chaque terme augmente en se basant sur la somme de ses deux prédécesseurs, formant une progression intéressante qui trouve de nombreuses applications dans des domaines tels que la théorie des nombres, l’analyse algorithmique, et au-delà.
Propriétés de la suite de Lucas
La suite de Lucas possède plusieurs propriétés remarquables qui la rendent utile pour une multitude d’applications mathématiques. En voici quelques-unes.
Relation avec la suite de Fibonacci
Une des propriétés les plus intéressantes de la suite de Lucas est sa relation étroite avec la suite de Fibonacci \((F_n)_{n \in \mathbb{N}}\), définie par \(F_{n} = F_{n-1} + F_{n-2}\) avec \(F_{0} = 0\) et \(F_{1} = 1\).
Pour tout nombre entier \(n \ge 2\), la suite de Lucas et la suite de Fibonacci sont liées par la formule :
\[L_{n} = F_{n-1} + F_{n+1}\]
Cette relation souligne le lien profond entre ces deux séquences et permet d’explorer des propriétés mathématiques avancées à travers leur interaction.
Relation entre les nombres de Lucas, Fibonacci et le nombre d’or
La formule de Binet pour les nombres de Fibonacci et celle analogue pour les nombres de Lucas révèlent une relation avec le nombre d’or \( \phi \).
On trouve que \( \phi^n \) peut être exprimé via les nombres de Lucas et de Fibonacci par \( \displaystyle \phi^n = \frac{L_n + F_n\sqrt{5}}{2} \). Cette formule illustre l’interconnexion profonde entre ces éléments mathématiques fondamentaux.
Formule explicite
Bien que la suite de Lucas soit définie récursivement, il existe une formule explicite pour trouver n’importe quel terme de la suite sans calculer tous les termes précédents. Cette formule, connue sous le nom de formule de Binet pour la suite de Lucas, est similaire à celle de la suite de Fibonacci :
\[L_{n} = \phi^n + \beta^n \; \text{ou encore} \; L_{n} = \phi^n +(-\phi)^{-n} \]
où \(\displaystyle \phi = \frac{1 + \sqrt{5}}{2}\) et \( \displaystyle \beta = \frac{1 – \sqrt{5}}{2}\) sont les racines de l’équation \(x^2 – x – 1 = 0\).
Liens entre les nombres de Lucas et les nombres de Fibonacci
Chaque terme de la suite de Lucas est étroitement lié à ceux de la suite de Fibonacci par la relation \( L_n = F_{n-1} + F_{n+1} \), ce qui illustre la complémentarité de ces deux suites célèbres. Cela met en lumière des relations algébriques entre les suites de Lucas et de Fibonacci, soulignant leur interaction et les motifs récurrents qui caractérisent ces séquences numériques intrigantes.
- En étudiant la valeur de la suite de Lucas dont l’indice est la somme de deux indices quelconques, \( L_{m+n} \), nous découvrons une interdépendance avec la suite de Fibonacci exprimée par \( L_{m+n} = L_{m+1}F_{n} + L_{m}F_{n-1} \).
- L’identité remarquable \( L_n^2 = 5F_n^2 + 4(-1)^n \) nous montre que les carrés des termes de Lucas peuvent être exprimés en fonction des carrés des termes de la suite de Fibonacci.
- La suite \( \frac{L_n}{F_n} \) converge vers \( \sqrt{5} \), révélant une harmonie mathématique et une constante remarquable au cœur de ces relations.
- Des formules impliquant des produits croisés, comme \( F_{2n} = L_nF_n \) et \( F_{3n} = (L_{2n} + (-1)^n)F_n \), soulignent l’interconnexion multiplicative entre les suites.
- De plus, les combinaisons linéaires des suites de Lucas et de Fibonacci, telles que \( F_{n+k} + (-1)^kF_{n-k} = L_kF_n \) et \( L_{n+k} – (-1)^kL_{n-k} = 5F_kF_n \), offrent des perspectives sur la symétrie et les propriétés récursives des suites.
Divisibilité dans la suite de Lucas
La divisibilité des nombres de Lucas offre un champ d’étude aussi riche que fascinant. Pour explorer cette propriété, on peut considérer la suite des restes d’un nombre de Lucas \( L_n \) lorsqu’on le divise par un entier \( a \). Cette suite suit la même relation de récurrence que la suite de Lucas, c’est-à-dire \( r_n = r_{n-1} + r_{n-2}. \)
On démontre également que les nombres de Lucas ne sont pas divisibles par un nombre de Fibonacci \( F_n \) plus grand ou égal à \( 5 \), un fait qui souligne les intrigantes propriétés de divisibilité qui se manifestent au sein de ces suites numériques classiques.
Conclusion
La suite de Lucas, avec ses propriétés uniques et ses multiples applications, est un sujet captivant d’étude en mathématiques. Sa relation étroite avec la suite de Fibonacci enrichit encore plus son étude, offrant aux étudiants un objet d’étude propice aux sujets de concours. Pour les étudiants en classes préparatoires préparant les épreuves parisiennes et les oraux de mathématiques, comprendre la suite de Lucas n’est pas seulement un exercice théorique, mais aussi une opportunité d’appliquer des résultats essentiels du programme dans des applications pratiques.
Pour maîtriser cette notion, tu peux faire le sujet Ecricome 2018 (mathématiques approfondies) qui aborde la suite de Fibonacci et qui est donc intimement lié à la suite de Lucas.
Tu peux retrouver ici toutes nos autres ressources mathématiques !