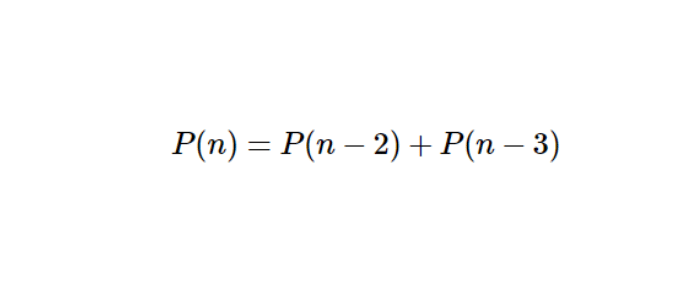La suite de Padovan est une suite d’entiers positifs dont les propriétés sont similaires à celles de la suite de Fibonacci. Cette notion est hors programme, mais elle peut tomber dans les épreuves de mathématiques parisiennes ou encore à Ecricome, dans une forme plus simple et guidée. Cet article t’aidera à mieux comprendre cette suite méconnue.
Introduction
La suite de Padovan a été nommée d’après le mathématicien italien Richard Padovan. Bien qu’il n’ait pas « inventé » cette suite, il l’a popularisée dans ses travaux sur les relations entre les mathématiques et l’architecture.
Richard Padovan a notamment exploré des liens entre cette suite et des structures esthétiques ou géométriques.
Définition de la suite de Padovan
La suite de Padovan \( P(n) \) est définie de manière récursive \( \forall n \in \mathbb{N} \) et \(n \geq 3\) par :
\[
P(n) = P(n-2) + P(n-3)
\]
Avec les conditions initiales :
\[
P(0) = 1, \quad P(1) = 1, \quad P(2) = 1
\]
Cela signifie que chaque terme de la suite est la somme des deux termes qui se trouvent deux et trois positions avant lui. Contrairement à la suite de Fibonacci, où chaque terme est la somme des deux précédents immédiats, la suite de Padovan met l’accent sur les écarts. Elle a donc une croissance plus lente.
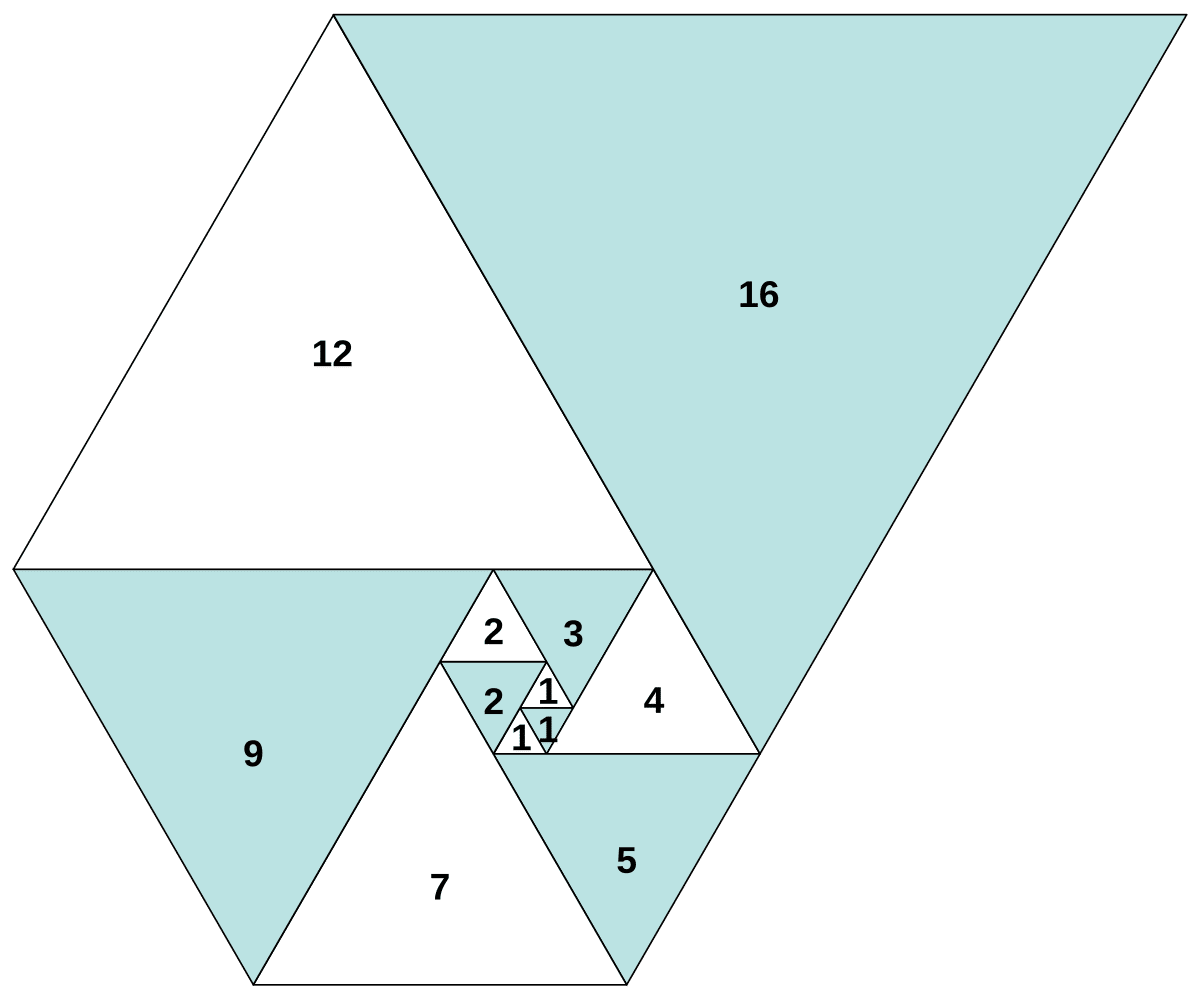
Les premiers termes de la suite de Padovan sont : \( 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, 151, \dots \)
Par exemple :
\( P(3) = P(1) + P(0) = 1 + 1 = 2 \)
\( P(4) = P(2) + P(1) = 1 + 1 = 2 \)
\( P(5) = P(3) + P(2) = 2 + 1 = 3 \)
Propriétés de la suite de Padovan
Croissance exponentielle
Bien que la suite de Padovan ait une croissance plus lente que la suite de Fibonacci, elle présente tout de même un taux de croissance exponentiel. Le rapport entre deux termes consécutifs de la suite converge vers une constante appelée « rapport plastique », notée \( \rho \).
On a : \[ \rho = 1.3247 \]
Le rapport plastique est la solution de l’équation :
\[
x^3 = x + 1
\]
Pour en savoir plus sur le nombre plastique, tu peux consulter cet article.
Lien avec la géométrie
Comme la suite de Fibonacci, la suite de Padovan a des applications en géométrie, notamment dans l’étude de proportions esthétiques et de motifs géométriques. Le rapport plastique associé à la suite de Padovan est ainsi parfois utilisé dans le design et l’architecture pour ses propriétés esthétiques similaires au nombre d’or.
On peut représenter la suite de Padovan comme ceci :
Utilisation de la matrice compagnon
La suite de Padovan peut être calculée de manière analogue à la suite de Fibonacci en utilisant une puissance de matrice.
On utilise une matrice spécifique, appelée « matrice compagnon », qui permet de représenter la règle de récurrence de la suite de Padovan. Cette matrice pour la suite de Padovan est :
\[
A = \begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 1 & 0 \end{pmatrix}
\]
Cette matrice encode le fait que chaque terme de la suite est la somme de deux termes précédents : \( P_n = P_{n-2} + P_{n-3} \).
On commence avec un vecteur initial représentant les trois premiers termes de la suite de Padovan :
\[
V_0 = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}
\]
Ce vecteur correspond aux valeurs de départ \( P_0 = 1 \), \( P_1 = 1 \) et \( P_2 = 1 \).
En multipliant cette matrice compagnon \( A \) par elle-même plusieurs fois (ce qui revient à élever la matrice à la puissance \( n \)), puis en multipliant par le vecteur initial, on obtient les termes suivants de la suite. Ainsi, en élevant \( A \) à la puissance \( n \) et en multipliant par \( V_0 \), on obtient un vecteur :
\[
A^n \times V_0 = \begin{pmatrix} P_n \\ P_{n+1} \\ P_{n+2} \end{pmatrix}
\]
qui contient les termes \( P_n \), \( P_{n+1} \) et \( P_{n+2} \) de la suite de Padovan.
Formule de Binet et suite de Padovan
La formule de Binet est une expression explicite permettant de calculer le \(n\)-ième terme d’une suite définie par une relation de récurrence, sans avoir besoin de connaître tous les termes précédents. Elle est célèbre pour son utilisation dans la suite de Fibonacci, mais des approches similaires existent pour d’autres suites récurrentes, comme la suite de Padovan.
Comme pour la suite de Fibonacci, on peut trouver donc une expression explicite du terme général de la suite de Padovan grâce à des racines caractéristiques. Cette formule est cependant plus complexe que celle de Fibonacci.
Les racines caractéristiques pour la suite de Padovan, trouvées en résolvant l’équation caractéristique du polynôme associé, sont données par :
\[
x^3 = x + 1
\]
ce qui donne les trois racines nécessaires à la formule.
La formule de Binet pour le terme général \(P_n\) de la suite de Padovan peut s’exprimer de manière simplifiée sous la forme :
\[
P_n = a \alpha^n + b \beta^n + c \gamma^n
\]
où : \(\alpha\), \(\beta\) et \(\gamma\) sont les racines de l’équation caractéristique \(x^3 = x + 1\), et : \(a\), \(b\), et \(c\) sont des constantes déterminées par les conditions initiales de la suite.
Cette formule est principalement théorique, car elle n’est pas aussi simple à appliquer directement pour des calculs.
Exemple avec le calcul de \(P_7\)
Pour illustrer comment on utilise cette formule, voici une approximation de \(P_7\) :
Soit \( \alpha \approx 1.3247 \), une des racines réelles de l’équation.
Si l’on utilise cette valeur seule (comme approximation), on obtient une estimation pour \(P_7\) en calculant directement \( \alpha^7 \).
Bien que cette méthode ne donne pas une réponse entière parfaite, elle aide à comprendre comment la suite se comporte de façon asymptotique. En pratique, \(P_7 = 5\), comme on l’a vu dans la liste des premiers termes, mais ce calcul approximatif montre comment la suite de Padovan croît.
Pour aller plus loin sur Padovan
La suite de Padovan étant très liée à celle de Fibonacci, tu peux t’entraîner sur ces exercices :
- Ecricome 2018 (mathématiques approfondies)
- Maths 1 HEC 2009 (mathématiques appliquées)
- La première Question Sans Préparation des Oraux HEC 2023
Tu peux retrouver ici le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder ici à toutes nos autres ressources mathématiques.