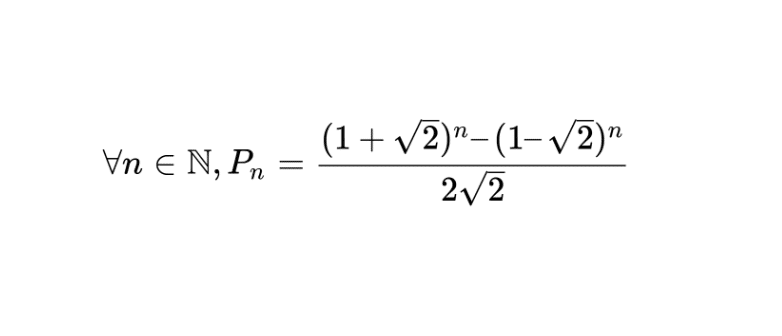La suite de Pell est une suite célèbre liée aux suites de Lucas et de Fibonacci. Derrière la simplicité de sa définition par récurrence se cachent des nombres intéressants, comme le célèbre nombre d’argent, que nous étudierons dans cet article. Il sera également question de quelques-unes de ses autres jolies propriétés que nous étudierons aussi. Enfin, nous mentionnerons la suite de Pell-Lucas qui est très proche de la suite de Pell.
Introduction à la suite de Pell
Tu connais sûrement déjà la très célèbre suite de Fibonacci. Cette dernière est définie de manière récurrente : chaque terme est la somme des deux termes qui le précèdent, avec les deux premiers termes fixés à 0 et 1. Formellement, on écrit :
\[F_0 = 0, \quad F_1 = 1\]
\[F_n = F_{n-1} + F_{n-2}, \quad \text{pour } n \geq 2.\]
Comme tu le verras lors de la définition proposée, la suite de Pell est extrêmement proche de la suite de Fibonacci, de sorte que ces dernières possèdent un grand nombre de propriétés en commun (suite de Fibonacci liée au nombre d’or, suite de Pell liée au nombre d’argent, par exemple).
Portée de la notion
Comme nous l’avons déjà dit, la suite de Pell est très proche des suites de Pell-Lucas et de Fibonacci, puisqu’elle partage avec ces dernières des propriétés très intéressantes. Comme nous n’aborderons que la suite de Pell dans cet article, je ne peux que t’inviter à jeter un coup d’œil aux articles sur la suite de Lucas et la suite de Fibonacci pour voir les subtilités liées à ces deux suites de renom !
Précisons également que, si la suite de Pell est en soi hors programme, son étude peut être partiellement réalisée avec les outils du programme. Pour ce qui ne peut pas être fait avec les outils du programme, il existe déjà plusieurs articles chez Major-Prépa à leur sujet.
Définition
Si cet article porte essentiellement sur la suite de Pell, nous étudierons également une suite extrêmement proche (tu comprendras directement pourquoi en voyant leur définition) du nom de « suite de Pell-Lucas ». Voici donc la définition de ces deux suites.
Suite de Pell
La suite de Pell \(P_n\) est définie par récurrence linéaire double : \[ P_n = \begin{cases} 0 & \text{pour } n = 0, \\ 1 & \text{pour } n = 1, \\ 2P_{n-1} + P_{n-2} & \text{pour } n \geq 2, \end{cases} \]
Suite de Pell-Lucas
De manière analogue, on pourra définir la suite de Pell-Lucas \(Q_n\) par la relation de récurrence double suivante :
\[ Q_n = \begin{cases} 2 & \text{pour } n = 0, \\ 2 & \text{pour } n = 1, \\ 2Q_{n-1} + Q_{n-2} & \text{pour } n \geq 2. \end{cases} \]
Pour rappel, la suite de Fibonacci est définie comme la somme de ses deux termes précédents. Ici, la croissance de la suite est d’autant plus grande que le terme précédent est multiplié par \(2\) dans la définition de la suite de Pell. Je te laisse donc comparer les premiers termes de la suite de Pell avec ceux de la suite de Fibonacci \(F_n\).
\(
\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline
F_0 & F_1 & F_2 & F_3 & F_4 & F_5 & F_6 & F_7 & F_8 & F_9 & F_{10} & F_{11} & F_{12} & F_{13} & F_{14} & F_n \\ \hline
0 & 1 & 1 & 2 & 3 & 5 & 8 & 13 & 21 & 34 & 55 & 89 & 144 & 233 & 377 & F_{n-1} + F_{n-2} \\ \hline
\end{array}
\)
\(
\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline
P_0 & P_1 & P_2 & P_3 & P_4 & P_5 & P_6 & P_7 & P_8 & P_9 & P_{10} & P_{11} & P_{12} & P_{13} & P_{14} & P_n \\ \hline
0 & 1 & 2 & 5 & 12 & 29 & 70 & 169 & 408 & 985 & 2378 & 5741 & 13860 & 33461 & 80782 & 2P_{n-1} + P_{n-2} \\ \hline
\end{array}
\)
Propriétés
Terme général
Il est également possible de déterminer le terme général de la suite de Pell à l’aide de la formule de Binet (qui est hors programme). Pour mémoire, cette formule permet également de déterminer le terme général de la suite de Fibonacci, mais également celui de la suite de Pell et de la suite de Pell-Lucas. En utilisant cette dernière, on trouve que :
\[\forall n \in \mathbb{N}, P_n = \frac{(1 + \sqrt{2})^n – (1 – \sqrt{2})^n}{2\sqrt{2}}\]
De manière analogue, on trouve le terme général de la suite de Pell-Lucas :
\[\forall n \in \mathbb{N}, Q_n = (1 + \sqrt{2})^n + (1 – \sqrt{2})^n \]
Il s’ensuit donc tout naturellement que l’on a : \(\forall n \in \mathbb{N}, 2\sqrt{2}P_n = Q_n\)
Formule alternative du terme général
Il est également possible de définir la suite \(P_n\) de manière différente. Cette formule reste toutefois très proche de celle donnée précédemment :
\[ P_n = \left\lfloor \frac{(1 + \sqrt{2})^n}{2\sqrt{2}} \right\rceil \quad \text{pour tout } n, \text{ où } \lfloor \cdot \rceil \text{ désigne l’entier le plus proche.} \]
Encore une fois, ce qui est possible pour la suite de Pell l’est aussi pour la suite de Pell-Lucas, on a donc en l’espèce :
\( Q_n = \lceil (1 + \sqrt{2})^n \rceil \forall n \geq 2 \) où \( \lceil \cdot \rceil\) désigne la partie entière supérieure.
Polynôme de Fibonacci et de Lucas
Les suites de Pell et de Pell-Lucas sont également liées à deux familles de polynômes : polynômes de Fibonacci et polynômes de Lucas. Voici leur définition avant d’établir le lien entre ces polynômes et les suites de Pell et Pell-Lucas.
C’est par une relation de récurrence linéaire que l’on peut définir les polynômes de Fibonacci :
\[F_n(x) =\begin{cases}0, & \text{si } n = 0 ; \\1, & \text{si } n = 1 ; \\xF_{n-1}(x) + F_{n-2}(x), & \text{si } n \geq 2.\end{cases}\]
\( F_n \) est un polynôme de degré \( n-1 \).
De manière analogue, la même relation de récurrence permet de définir la suite de Lucas, mais avec des valeurs initiales différentes et variables :
\[L_n(x) =\begin{cases}2, & \text{si } n = 0 ; \\x, & \text{si } n = 1 ; \\xL_{n-1}(x) + L_{n-2}(x), & \text{si } n \geq 2.\end{cases}\]
\( L_n \) est un polynôme de degré \( n \).
Ainsi, on déduit directement de la définition des polynômes et des suites de Pell et Pell-Lucas que l’on a les propriétés suivantes :
\[P_n = F_n(2) \quad \text{et} \quad Q_n = L_n(2)\]
Ce qui est très intéressant avec cette propriété, c’est qu’il est souvent plus simple d’étudier des polynômes et que, de la sorte, il est possible de déduire de l’étude des polynômes des propriétés intéressantes sur la suite de Pell et celle de Pell-Lucas.
Lien avec le nombre d’argent
Pour établir le lien entre la suite de Pell et le nombre d’argent, il convient d’étudier le rapport des termes successifs de la suite \(P_n\), c’est-à-dire d’étudier \(\forall n \in \mathbb{N}, \frac{P_{n+1}}{P_n}\). On obtient alors la propriété suivante :
\[ \lim_{n \to \infty} \frac{P_{n+1}}{P_n} = \delta_s = 1 + \sqrt{2} \]
Ou, pour rappel, \( \delta_s = 1 + \sqrt{2} \approx 2.414 = 2 + \frac{1}{2 + \frac{1}{2 + \frac{1}{2 + \frac{1}{2 + \dots}}}} \)
Conclusion
En définitive, la suite de Pell est une suite fondamentale des mathématiques, notamment en ce qu’elle est liée à la suite de Fibonacci et partage plusieurs propriétés intéressantes avec celle-ci. Le rapport des termes de la suite de Pell tend également vers le nombre d’argent, ce qui fait une énième propriété pertinente de la suite de Pell.
Il n’y a désormais plus qu’à espérer que cette notion tombe le jour J aux concours !
Tu peux retrouver le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder à toutes nos autres ressources mathématiques !