La suite de Perrin est une suite d’entiers positifs relativement simple dont les propriétés sont similaires à celles de la suite de Fibonacci. Elle suit la même relation de récurrence que la suite de Padovan. Bien qu’elle ne soit pas présente dans le programme de mathématiques d’ECG, cette notion peut être utile à savoir pour préparer au mieux les épreuves parisiennes. Cet article est là pour t’aider à y voir plus clair !
Introduction
En 1899, François Olivier Raoul Perrin propose une suite récurrente, aujourd’hui appelée suite de Perrin, pour tester la primalité des nombres. Selon lui, si \(n\) est premier, alors \(P(n) \) est divisible par \( n \).
Bien que cela fonctionne pour de nombreux nombres, un contre-exemple a été trouvé en 1982 par Adams et Shanks, montrant que cette propriété ne garantit pas toujours la primalité.
Définition de l’inégalité de Perrin
La suite de Perrin \( P(n) \) est définie de manière récursive \( \forall n \in \mathbb{N} \) et \(n \geq 3\) par :
\[
P(n) = P(n-2) + P(n-3)
\]
Avec les conditions initiales :
\[
P(0) = 3, \quad P(1) = 0, \quad P(2) = 2
\]
Les premiers termes de la suite de Perrin sont : \( 3, 0, 2, 3, 2, 5, 5, 7, 10, 12, 17, 22, 29, 39, 51, 68, 90 \dots \)
Par exemple :
\( P(3) = P(1) + P(0) = 0 + 3 = 3 \)
\( P(4) = P(2) + P(1) = 2 + 0 = 2 \)
\( P(5) = P(3) + P(2) = 3 + 2 = 5 \)
Propriétés sur l’inégalité de Perrin
Lien avec la géométrie et relation d’ordre 5
La suite de Perrin suit aussi une autre relation, appelée relation de récurrence d’ordre 5 :
\[
P_n = P_{n-1} + P_{n-5}
\]
Cette relation signifie qu’à partir de \( n = 5 \), chaque terme est la somme du terme précédent (\(P_{n-1}\)) et du terme cinq positions avant (\(P_{n-5}\)).
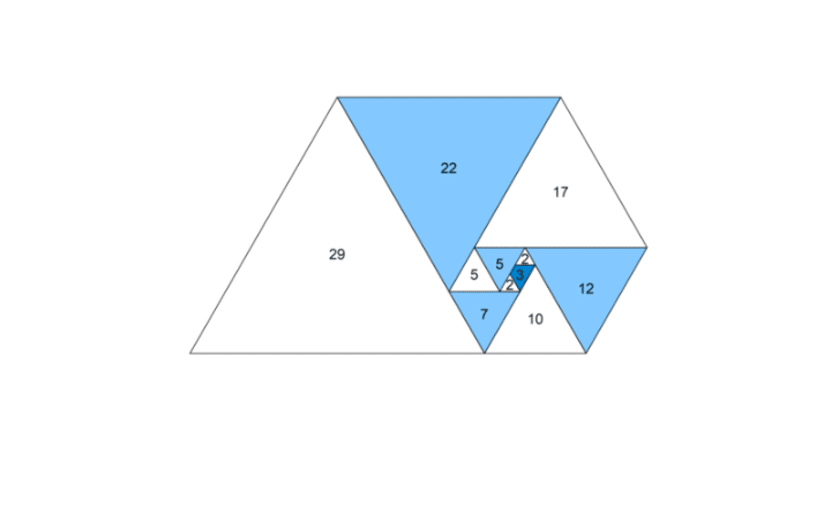
Pour visualiser cette suite, on peut créer une construction en spirale avec des triangles équilatéraux en suivant ce procédé.
On commence par un triangle équilatéral de côté \( P_2 = 2 \).
On place ensuite un triangle équilatéral de côté \( P_3 = 3 \), mais on le tronque d’un petit triangle de côté 1.
Puis on place un triangle de côté \( P_4 = 2 \).
En suivant la suite de Perrin, chaque nouveau triangle ajoute une section à la spirale, en respectant la longueur définie par les termes de la suite.
On obtient alors cette spirale :
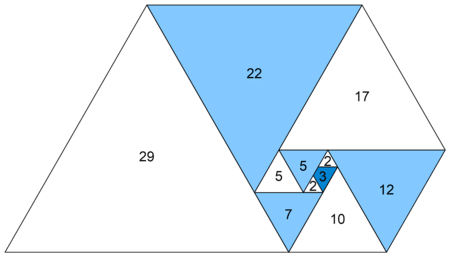
On observe que cette représentation graphique est très similaire à celle de la suite de Padovan. Dans les deux cas, la spirale formée montre la croissance et le motif récurrent des suites, mais les longueurs de chaque segment suivent des règles spécifiques à chaque suite.
Utilisation de la matrice compagnon
La suite de Perrin peut être calculée de manière analogue à la suite de Fibonacci en utilisant une puissance de matrice.
On utilise une matrice spécifique, appelée matrice compagnon, qui permet de représenter la règle de récurrence de la suite de Perrin.
Le polynôme caractéristique associé à la suite de Perrin est : \( x^(3) – x – 1 = 0 \)
La matrice compagnon associée à ce polynôme est : \(
A = \begin{pmatrix} 0 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix} \)
Cette matrice encode le fait que chaque terme de la suite est la somme de deux termes précédents : \( P_n = P_{n-2} + P_{n-3} \).
On commence avec un vecteur initial représentant les trois premiers termes de la suite de Perrin :
\[
V_0 = \begin{pmatrix} 3 \\ 0 \\ 2 \end{pmatrix}
\]
Ce vecteur correspond aux valeurs de départ \( P_0 = 3 \), \( P_1 = 0 \) et \( P_2 = 2 \).
En multipliant cette matrice compagnon \( A \) par elle-même plusieurs fois (ce qui revient à élever la matrice à la puissance \( n \)), puis en multipliant par le vecteur initial, on obtient les termes suivants de la suite. Ainsi, en élevant \( A \) à la puissance \( n \) et en multipliant par \( V_0 \), on obtient un vecteur :
\[
A^n \times V_0 = \begin{pmatrix} P_n \\ P_{n+1} \\ P_{n+2} \end{pmatrix}
\]
qui contient les termes \( P_n \), \( P_{n+1} \) et \( P_{n+2} \) de la suite de Perrin.
La formule de Binet et la suite de Perrin
La formule de Binet est une formule qui permet de calculer directement le \( n \)-ième terme d’une suite récurrente, comme la suite de Perrin, sans avoir à calculer tous les termes précédents.
Les racines caractéristiques pour la suite de Padovan, trouvées en résolvant l’équation caractéristique du polynôme associé, sont données par :
\[
x^3 = x + 1
\]
ce qui donne les trois racines nécessaires à la formule.
La formule de Binet pour le terme général \(P_n\) de la suite de Perrin peut s’exprimer de manière simplifiée sous la forme :
\[
P_n = a \alpha^n + b \beta^n + c \gamma^n
\]
où : \(\alpha\), \(\beta\) et \(\gamma\) sont les racines de l’équation caractéristique \(x^3 = x + 1\),
et : \(a\), \(b\) et \(c\) sont des constantes déterminées par les conditions initiales de la suite.
En pratique, cette formule est compliquée à appliquer manuellement.
Divisibilité
Si \(n\) est un nombre premier, alors \(n\) divise \( P(n) \). Cette propriété a été démontrée par Lucas en 1876 (pour plus de détails, tu peux consulter cet article).
En revanche, on ne sait pas si \(n\) divisant \( P(n) \), le nombre \(n\) est premier. Si c’est le cas, le nombre est appelé pseudo-premier de Perrin.
Algorithme Python de la suite de Perrin
On peut simuler la suite de Perrin de plusieurs manières avec Python. En voici une très simple :
Pour aller plus loin sur Perrin
La suite de Perrin étant très liée à celle de Fibonacci, tu peux t’entraîner sur ces exercices :
- Ecricome 2018 (mathématiques approfondies)
- Maths 1 HEC 2009 (mathématiques appliquées)
- La première Question Sans Préparation des Oraux HEC 2023
Tu peux retrouver ici le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder ici à toutes nos autres ressources mathématiques.