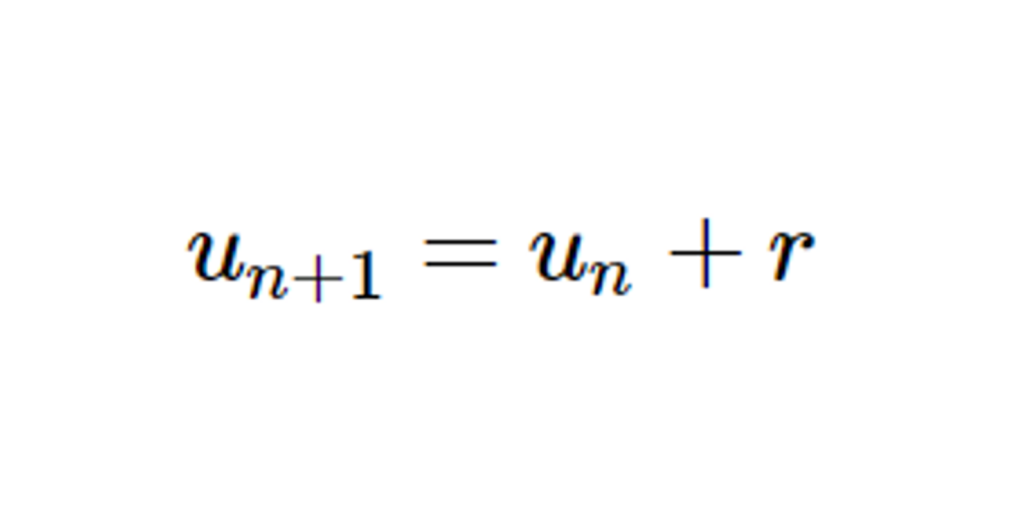Les suites arithmétiques sont les suites les plus simples. Il est donc important de les maîtriser pour ne pas perdre de points le jour du concours. Pour ce faire, tu verras dans cet article tout ce qu’il faut savoir sur ces suites. Promis, ces dernières n’auront plus aucun secret pour toi !
Qu’est-ce qu’une suite arithmétique ?
Une suite arithmétique est une suite de nombres ayant la particularité suivante : pour passer d’un terme de la suite au suivant, on ajoute ou on retire toujours le même nombre. Ce nombre en question s’appelle la raison (qu’on notera ensuite « r »).
On peut donc formaliser cette définition en français de façon plus rigoureuse. Une suite arithmétique est une suite \( (u_n)\) pour laquelle il existe un réel r, indépendant de n, tel que : \(\forall n \in\mathbb{N}, u_{n+1} = u_n + r.\)
Par exemple, si on note \( u_0 = 1, u_1 = 3, u_2= 5, u_3 = 7\), on remarque que c’est une suite arithmétique de raison 2, car on ajoute toujours 2 pour passer d’un terme au suivant.
Forme explicite d’une suite arithmétique
Maintenant qu’on a compris comment fonctionne une suite arithmétique, on a envie de l’écrire de façon explicite, c’est-à-dire sous la forme suivante : \(\forall n \in\mathbb{N}, u_{n} = truc .\)
Or, on sait, par exemple, que pour atteindre le terme \(u_3\) d’une suite arithmétique \((u_n)\), on part du premier terme qu’on note \(u_o\), auquel on ajoute trois fois la raison (si on ajoute une fois la raison, on a \(u_1\), si on ajoute deux fois la raison, on a \(u_2\), etc.). On a alors \( u_3 = u_0 + 3r\).
De façon générale, on peut donc dire que si \((u_n)\) est une suite arithmétique de raison r, alors \(\forall n \in\mathbb{N}, u_{n} = u_0 + nr.\)
(La démonstration est assez triviale : il faut faire une récurrence simple et utiliser la définition d’une suite arithmétique pour montrer l’hérédité.)
On peut même généraliser cette formule pour les suites arithmétiques \((u_n)\) qui ne commencent pas au terme \(u_0\), mais au terme \(u_p\), \(p\in\mathbb{N}.\)Cela nous donne : \(\forall n \ge p, u_{n} = u_p + (n-p)r.\)
(Encore la même démonstration…)
Comment déterminer une suite arithmétique ?
Si on a une suite \((u_n)\) et qu’on veut savoir si cette suite est arithmétique ou non, c’est très simple : il suffit de calculer pour \( n\in\mathbb{N}, u_{n+1}-u_n\). Si le résultat est une constante, alors la suite est arithmétique et la constante trouvée correspond à la raison de la suite.
Sens de variation et limite d’une suite arithmétique
Le sens de variation et la limite d’une suite arithmétique dépendent de la raison r.
- Si r > 0, alors \((u_n)\) est strictement croissante et la suite diverge vers \(+\infty.\)
- Si r < 0, alors \((u_n)\) est strictement décroissante et la suite diverge vers \(-\infty.\)
- Si r = 0, alors \((u_n)\) est constante et est égale à son premier terme.
(La monotonie se démontre très facilement en calculant \(u_{n+1}-u_n\) et la limite en \(+\infty\) se montre en faisant tendre \(n\) vers \(+\infty\) dans la forme explicite.)
Propriété bonus
Si \((u_n)\) est une suite arithmétique de premier terme \(u_0\), on peut montrer que la somme \( u_0 + u_1 + … + u_n\) est égale au nombre de termes, multiplié par la moyenne des deux extrémités, c’est-à-dire \(\displaystyle \frac{u_0 +u_n}
{2}(n+1).\)
Démonstration
\(\begin{align}u_0 + u_1 + … + u_n &= \displaystyle \sum_{k=0}^{n}u_k \\
&= \displaystyle \sum_{k=0}^{n}(u_0+kr)\\ &= (n+1)u_0 + \displaystyle \frac{n(n+1)r}{2}\\ \end{align}\)
(On utilise la forme explicite de \((u_n)\), puis la linéarité de la somme et enfin la formule de la somme des entiers naturels.)
On a également : \(\displaystyle \frac{u_0 +u_n}{2}(n+1) = \displaystyle \frac{(n+1)(2u_0 +rn)}{2} = \displaystyle \frac{n(n+1)r}{2} + (n+1)u_0\)
(On utilise la forme explicite de \((u_n)\), puis on développe et on sépare les fractions.)
On a donc \( u_0 + u_1 + … + u_n = \displaystyle \frac{u_0 +u_n}{2}(n+1).\)
Les suites arithmétiques sur Python
Sur Python, il est assez fréquent de tomber sur une question dans laquelle on te demande de coder une suite arithmétique. Or, comme tu vas le voir, il est très simple de réaliser ce programme ; il serait donc dommage de ne pas récupérer ces points !
Voici un programme qui permet de renvoyer le \(n^{ième}\) terme d’une suite arithmétique \((u_{n})\) de raison 2 et de premier terme \(u_{0} = 1\):
Pour décrire brièvement le programme, la deuxième ligne correspond au terme \(u_{0}\) de notre suite. La troisième ligne a pour objectif de nous faire passer du terme \(u_{0}\) au terme \(u_{n}\) souhaité (on remarque que range va de 1 à n+1 ; il ne faut pas oublier que Python s’arrête à la valeur du dernier terme \(\color{blue}{-1}\), c’est-à-dire n+1 \(\color{blue}{-1}\) = n. Enfin, la quatrième ligne est peut-être la plus surprenante. Il faut savoir que l’écriture de cette ligne est équivalente à celle-ci : u = u + 2. Écrite sous cette forme, on remarque aisément que la quatrième ligne applique la relation d’hérédité qui définit une suite arithmétique, c’est-à-dire \(u_{n+1} = u_{n} + r\), avec r = 2 en l’occurrence.
On remarque que l’on peut facilement généraliser ce programme pour toutes les suites arithmétiques. En effet, il suffit de modifier la deuxième et la quatrième ligne, en affectant respectivement la valeur du premier terme \(u_{0}\) d’une suite considérée, au lieu du \(\color{red}{1}\), et la raison de la suite considérée, à la place du \(\color{red}{2}\).
Conclusion
Tu as désormais tous les outils nécessaires pour pouvoir attaquer sereinement les exercices comprenant cette notion.
Tu peux retrouver ici le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder ici à toutes nos autres ressources mathématiques !