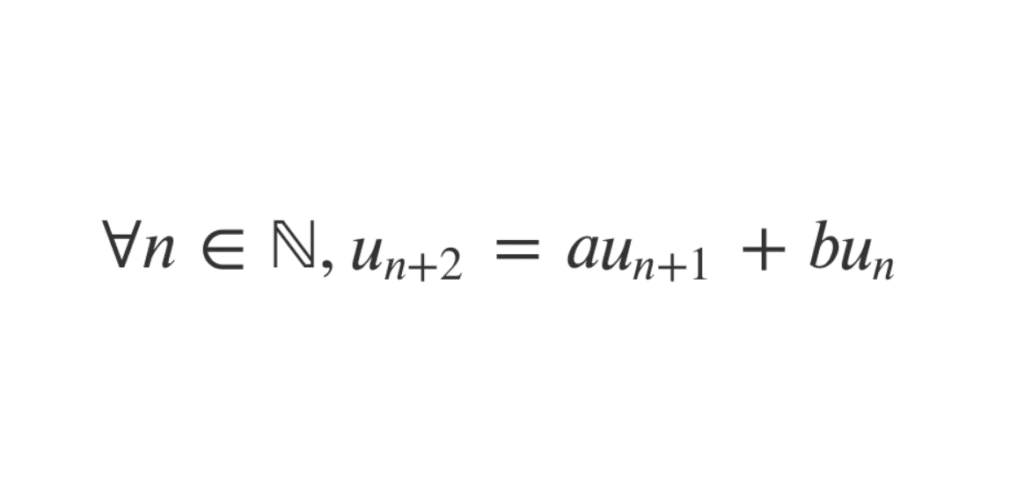Dans cet article, on va s’intéresser aux suites récurrentes linéaires d’ordre 2. Bonne lecture !
Définition des suites récurrentes linéaires d’ordre 2
On appelle suite récurrente linéaire d’ordre 2 une suite \((u_n)_{n \in \mathbb{N}}\) définie par :
\(\forall n \in \mathbb{N}, u_{n+2} = au_{n+1} + bu_{n}\).
La suite \((u_{n+2})_{n \in \mathbb{N}}\) est une combinaison linéaire de \((u_{n+1})_{n \in \mathbb{N}}\) et \((u_n)_{n \in \mathbb{N}}\).
On appelle équation caractéristique de \(u\) l’équation \(x² − ax − b = 0\).
Par exemple, la suite définie par :
\[\begin{cases} u_{0} =1 , u_{1} = 0 \\
u_{n+2} = 2u_{n+1} + u_{n} \end{cases}\]
est une suite récurrente linéaire d’ordre 2. Son équation caractéristique est l’équation :
\[x² = 2x + 1.\]
Terme général d’une suite récurrente linéaire d’ordre 2
Théorème associée aux SRL2
Soit \(u\) est une suite récurrente linéaire d’ordre 2 d’équation caractéristique \(x² – ax – b = 0\).
On suppose \(b \ne 0\). Alors, si on note \(\Delta\) le discriminant du trinôme
- Si \(\Delta > 0\) :
\( \ \ \ \ \ \ \ \) On note \(r_{1}\) et \(r_{2}\) les deux solutions de l’équation caractéristique.
\( \ \ \ \ \ \ \ \) Il existe alors \(\lambda\) et \(\mu\) deux réels tels que
\[\forall n \in \mathbb{N}, u_{n} = \lambda \ r_{1}^{n} + \mu \ r_{2}^{n}.\]
- Si \(\Delta = 0\) :
\( \ \ \ \ \ \ \ \) On note \(r\) l’unique solution de l’équation caractéristique.
\( \ \ \ \ \ \ \ \) Il existe alors \(\lambda\) et \(\mu\) deux réels tels que
\[\forall n \in \mathbb{N}, u_{n} = (\lambda + \mu * n) \ r^{n}.\]
Démonstration
On démontrera seulement le cas \(\Delta > 0\), le cas \(\Delta = 0\) étant très similaire.
Dans un premier temps, nous supposons que les valeurs de \(\lambda\) et \(\mu\) que nous cherchons existent. Nous étudions les conséquences de cette existence et cherchons à obtenir des informations sur ces nombres. Dans un second temps, nous utiliserons ces informations pour démontrer vraiment l’existence.
Si \((u_n)_{n \in \mathbb{N}}\) est une suite récurrente linéaire d’ordre 2 donnée par
\[\forall n \in \mathbb{N}, u_n = \lambda x_{1}^{n} + \mu x_{2}^{n},\]
alors on a nécessairement :
\(\begin{cases} u_{0} = \lambda + \mu \\
u_{1} = \lambda r_{1} + \mu r_{2} \end{cases} \ \ \ \ \ \Leftrightarrow \begin{cases} \lambda = u_{0} – \mu \\
u_{1} = \lambda r_{1} + \mu r_{2} \end{cases} \ \ \ \ \ \Leftrightarrow \begin{cases} \lambda = u_{0} – \mu \\
u_{1} = (u_0 – \mu) r_{1} + \mu r_{2} \end{cases}\)
\(\Leftrightarrow \begin{cases} \lambda = u_{0} – \mu \\
u_{1} = u_0 r_{1} + \mu (r_{2} – r_{1}) \end{cases} \ \ \ \ \ \Leftrightarrow \begin{cases} \lambda = u_{0} – \mu \\
\mu = \frac{u_1 – u_0 r_{1}}{r_{2} – r_{1}} \end{cases} \ \ \ \ \ \Leftrightarrow \begin{cases} \lambda = u_{0} – \frac{u_1 – u_0 r_{1}}{r_{2} – r_{1}} \\
\mu = \frac{u_1 – u_0 r_{1}}{r_{2} – r_{1}} \end{cases}\)
\(\Leftrightarrow \begin{cases} \lambda = u_{0} – \frac{u_1 – u_0 r_{2}}{r_{1} – r_{2}} \\
\mu = \frac{u_1 – u_0 r_{1}}{r_{2} – r_{1}} \end{cases}\)
Autrement dit, si jamais on montre que la suite \(u\) est de la forme \(\lambda r_1^n + \mu r_2^n\), alors les valeurs de \(\lambda\) et \(\mu\) doivent être celles que nous venons de trouver.
Synthèse
On pose donc :
\[\lambda = \frac{u_1 – u_0 r_2}{r_1 – r_2} \ \ \ \ \ \ \mu = \frac {u_1 – u_0 r_1}{r_2 – r_1}.\]
On pose, pour tout \(n\) entier naturel, \(P(n) : u_n = \lambda \ r_{1}^{n} + \mu \ r_{2}^{n}\). Démontrons, par une récurrence à deux étapes, que cette proposition est vraie pour tout \(n\).
Initialisation
On a choisi \(\lambda\) et \(\mu\) pour que \(P(0)\) et \(P(1)\) soient vraies.
Hérédité
Soit \(n \in \mathbb{N}\), on suppose \(P(n)\) et \(P(n+1)\) vraies. On a alors :
\(u_{n+2} = au_{n+1} + bu_n \qquad \qquad \qquad \qquad \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \) par définition de \(u\)
\( \quad \ \ \ \ = a(\lambda r_1^{n+1} + \mu r_2^{n+1}) + b(\lambda r_1^n + \mu r_2^n) \ \ \ \ \ \ \ \ \ \ \ \ \ \) par hypothèse de récurrence
\( \quad \ \ \ \ = \lambda (a r_1^{n+1} + b r_1^n) + \mu(ar_2^{n+1} + b r_2^n)\)
\( \quad \ \ \ \ = \lambda r_1^{n} (a r_1 + b) + \mu r_2^{n} (a r_2 + b)\)
\( \quad \ \ \ \ = \lambda r_1^{n} r_1^{2} + \mu r_2^{n} r_2^{2} \qquad \qquad \qquad \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \) car \(r_1\) et \(r_2\) sont des solutions de \(x² − ax − b = 0\)
\( \quad \ \ \ \ = \lambda r_1^{n+2} + \mu r_2^{n+2}\).
\(n\) étant arbitraire dans \(\mathbb{N}\), on a démontré
\[\forall n \in \mathbb{N}, (P(n) \ \text{et} \ P(n+1)) \Rightarrow P(n+2)\]
La proposition est donc héréditaire.
Conclusion
On a démontré par récurrence à deux étapes que
\[\forall n \in \mathbb{N}, u_n = \lambda r_1^n + \mu r_2^n.\]
Exemple d’une suite récurrente linéaire d’ordre 2
Soit \(u\) la suite définie par :
\[\begin{cases} u_{0} =0 , u_{1} = 1 \\
u_{n+2} = -u_{n+1} \ + \ 2u_{n}\end{cases}\]
L’équation caractéristique de cette suite est :
\[x² \ + x \ – \ 2.\]
On a \(\Delta = 1 \ – \ 4 * 1 * (-2) = 9 > 0\). Donc, on pose :
\[r_1 = \frac{-1 + \sqrt{9}}{2} = 1 \qquad \text{et} \qquad r_2 = \frac{-1 \ – \ \sqrt{9}}{2} = -2.\]
On a donc, d’après le théorème, qu’il existe \(\lambda\) et \(\mu\) deux réels tels que
\[\forall n \in \mathbb{N}, u_n = \lambda * 1^n + \mu * (-2)^n = \lambda + \mu * (-2)^n.\]
Pour trouver les valeurs de \(\lambda\) et \(\mu\), on se sert des deux premiers termes de \(u\). On a en effet :
\[u_0 = 0 \quad \text{donc} \quad u_0 = \lambda + \mu * (-2)^0\]
\[u_1 = 1 \quad \text{donc} \quad u_1 = \lambda + \mu * (-2)^1\]
Ce qui donne les deux équations :
\(\begin{cases} \lambda + \mu = 0 \\
\lambda \ – \ 2\mu = 1\end{cases} \qquad \Leftrightarrow \qquad \begin{cases} \lambda = -\mu \\
\lambda \ – \ 2\mu = 1\end{cases} \qquad \Leftrightarrow \qquad \begin{cases} \lambda = -\mu \\
\lambda + 2 \lambda = 1\end{cases}\)
\(\Leftrightarrow \ \begin{cases} \lambda = -\mu \\
3 \lambda = 1\end{cases}\qquad \Leftrightarrow \qquad \begin{cases} \mu = -\frac{1}{3} \\
\lambda = \frac{1}{3}\end{cases}\).
Finalement, on obtient que :
\[\forall n \in \mathbb{N}, u_n = \left(-\frac{1}{3}\right) * (-2)^n + \frac{1}{3} = \frac{1}{3} (1 \ – \ (-2)^n).\]
Retrouve toutes nos ressources mathématiques ici !