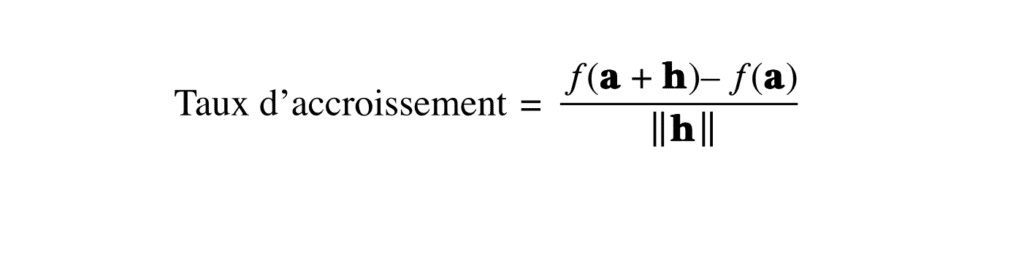Le taux d’accroissement pour des fonctions de \( n \) variables généralise le concept que nous connaissons pour une seule variable. Cette généralisation est cruciale pour analyser des fonctions dans des contextes multidimensionnels, typiques en économie et en sciences où les fonctions dépendent de plusieurs facteurs simultanément. Le taux d’accroissement est un concept fondamental en analyse mathématique, il est souvent utilisé pour mesurer la variation d’une fonction par rapport à ses variables. Dans cet article, nous explorerons l’utilisation du taux d’accroissement pour les fonctions d’une et de plusieurs variables, une compétence essentielle en analyse de par son lien étroit avec la dérivée.
Taux d’Accroissement pour une Variable
Définition et Formule
Pour une fonction \( f \) d’une seule variable \( x \), le taux d’accroissement entre deux points \( a \) et \( a+h \) (où \( h \neq 0 \)) est défini comme le rapport de la différence des valeurs de \( f \) aux points \( a \) et \( a+h \) sur \( h \). Formellement, il est exprimé par la formule :
\[
\text{Taux d’accroissement} = \frac{f(a+h) – f(a)}{h}
\]
Ce taux d’accroissement est souvent utilisé pour approximer la pente de la tangente à la courbe de la fonction au point \( a \), et s’approche de la dérivée de \( f \) au point \( a \) lorsque \( h \) tend vers zéro.
Définition du Taux d’Accroissement pour n Variables
Formulation Générale
Pour une fonction \( f: \mathbb{R}^n \rightarrow \mathbb{R} \), qui est une fonction des variables \( x_1, x_2, \ldots, x_n \), le taux d’accroissement autour d’un point \( a = (a_1, a_2, \ldots, a_n) \) dans la direction d’un vecteur \( h = (h_1, h_2, \ldots, h_n) \) est donné par:
\[
\text{Taux d’accroissement} = \frac{f(a + h) – f(a)}{\|h\|}
\]
où \( \|h\| \) est la norme du vecteur \( h \), souvent pris comme la norme euclidienne pour simplifier.
Interprétation, Gradient et Limite
Ce taux mesure la variation moyenne de la fonction \( f \) dans la direction de \( h \) par unité de longueur de \( h \). Lorsque \( h \) tend vers le vecteur nul, le taux d’accroissement tend vers le gradient de \( f \) au point \( a \), à condition que \( f \) soit différentiable au point \( a. \)
Égalité et Inégalité des Accroissements Finis
Voici les formulations symboliques de l’égalité et de l’inégalité des accroissements finis pour les fonctions d’une variable et de plusieurs variables :
Égalité des Accroissements Finis (pour une variable)
Pour une fonction \( f: [a, b] \rightarrow \mathbb{R} \) continuement différentiable sur l’intervalle fermé \([a, b]\) et différentiable sur l’intervalle ouvert \( ]a, b[ \), l’égalité des accroissements finis s’énonce comme suit :
\[
f(b) – f(a) = f'(c)(b – a)
\]
où \( c \) est un certain point dans l’intervalle \( (a, b) \).
Inégalité des Accroissements Finis (pour une variable)
Sous les mêmes conditions de continuité et différentiabilité :
\[
|f(b) – f(a)| \leq M |b – a|
\]
où \( M \) est un majorant de \( |f'(x)| \) sur \( [a, b] \).
Égalité des Accroissements Finis (pour plusieurs variables)
Pour une fonction \( f: \mathbb{R}^n \rightarrow \mathbb{R} \) différentiable, et pour deux points \( a, b \in \mathbb{R}^n \), il existe un point \( c \) sur le segment de droite joignant \( a \) et \( b \) tel que :
\[
f(b) – f(a) = \nabla f(c) \cdot (b – a)
\]
Inégalité des Accroissements Finis (pour plusieurs variables)
Sous l’hypothèse que \( f \) est différentiable sur un domaine contenant le segment joignant \( a \) et \( b \) :
\[
|f(b) – f(a)| \leq \sup_{x \in [a, b]} \|\nabla f(x)\| \cdot \|b – a\|
\]
où \( \|\cdot\| \) est la norme euclidienne.
Ces formulations montrent comment l’analyse locale, via les dérivées ou les gradients, peut être utilisée pour inférer des propriétés globales des fonctions.
Calcul du Taux d’Accroissement en Pratique
Exemple avec une Fonction de Deux Variables
Considérons une fonction économique \( f(x, y) = x^2y \). Pour trouver le taux d’accroissement au point \( (1,2) \) dans la direction \( (0.1, -0.1) \), calculez :
\[
\frac{f(1+0.1, 2-0.1) – f(1, 2)}{\sqrt{(0.1)^2 + (-0.1)^2}} = \frac{f(1.1, 1.9) – f(1, 2)}{\sqrt{0.02}}
\]
\[
= \frac{(1.1)^2 \cdot 1.9 – 1^2 \cdot 2}{\sqrt{0.02}} = \frac{2.299 – 2}{0.1414} \approx 2.115
\]
Generalisation à n Variables
Pour une fonction de \( n \) variables, la méthode reste analogue, mais avec une complexité accrue liée à la gestion de plusieurs variables. Les calculs deviennent souvent lourds sans l’aide d’outils informatiques pour les fonctions compliquées ou un grand nombre de variables.
Relation entre le Taux d’Accroissement et la Dérivée
Le taux d’accroissement pour des fonctions de \( n \) variables est intrinsèquement lié au concept de dérivée, un pilier de l’analyse en dimensions supérieures. Cette relation peut être éclaircie en considérant que le taux d’accroissement est en fait une généralisation de la dérivée à des espaces multidimensionnels.
De la Dérivée au Gradient
Pour une fonction d’une seule variable, le taux d’accroissement, comme discuté précédemment, converge vers la dérivée de la fonction à mesure que l’intervalle \( h \) se rapproche de zéro. Cette dérivée représente la pente de la tangente à la courbe de la fonction au point considéré, offrant une mesure instantanée de la vitesse de variation de la fonction.
En étendant ce concept à plusieurs variables, le taux d’accroissement, lorsque \( h \) tend vers le vecteur nul, converge vers le gradient de la fonction. Le gradient, noté \( \nabla f(a) \), est un vecteur dont chaque composante est la dérivée partielle de \( f \) par rapport à une des variables au point \( a \). Ainsi, le gradient est à la fonction multivariable ce que la dérivée est à la fonction univariable : il mesure la pente maximale de la fonction, mais dans toutes les directions de l’espace.
Signification du Gradient
Le gradient ne se contente pas de généraliser la dérivée; il fournit également une direction dans l’espace des variables où la fonction augmente le plus rapidement. De ce fait, comprendre le gradient revient à comprendre comment varier les paramètres pour maximiser ou minimiser une fonction, un enjeu central dans de nombreux domaines tels que l’optimisation économique et la recherche opérationnelle.
Cette profonde connexion entre le taux d’accroissement, la dérivée, et le gradient souligne l’importance de maîtriser ces concepts pour analyser et manipuler des fonctions qui dépendent de multiples variables, préparant ainsi les étudiants à des applications théoriques et pratiques rigoureuses.
Conclusion
Le taux d’accroissement pour des fonctions de \( n \) variables est un outil analytique puissant, permettant de comprendre comment une fonction réagit à des petits changements dans toutes les directions possibles. Cette compréhension est essentielle dans les applications où plusieurs variables interagissent souvent de manière complexe. Pratiquer le calcul de ces taux dans diverses situations renforcera ta maîtrise de l’analyse multidimensionnelle, te préparant efficacement pour les épreuves parisiennes et les oraux de mathématiques !
Pour t’entrainer sur ces notions tu peux réaliser les sujets mathématiques approfondies suivants :
Tu peux retrouver ici toutes nos autres ressources mathématiques !