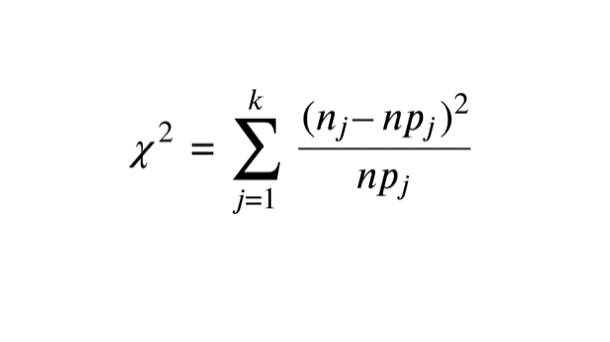Nous allons nous intéresser à une notion clé en statistiques : le test d’ajustement. Cette notion est particulièrement utile, car elle possède de nombreuses applications concrètes dans des domaines tels que la finance. Il existe de nombreux tests d’ajustement (le test de Kolmogorov-Smirnov, le test de Shapiro-Wilk, etc.) et le premier fut celui du khi-deux, développé en 1900 par l’Anglais Karl Pearson.
À quoi sert un test d’ajustement ?
Le test d’ajustement a pour but d’évaluer à quel point un modèle statistique correspond bien à des données observées.
Ainsi, ce test permet de déterminer si les différences entre les valeurs prédites par un modèle et les valeurs réelles sont simplement le résultat du hasard ou s’il existe des résultats importants à prendre en compte.
Le test d’ajustement du khi-deux
Le test d’ajustement du khi-deux est un grand classique dans le domaine des statistiques, car c’est le test d’ajustement le plus célèbre et le plus utilisé. Il compare une distribution théorique d’un caractère à une distribution observée.
Premièrement, notons \( C_1, …, C_k, k\) classes qui contiennent les valeurs observées, \(n_1, …, n_k \) l’effectif associé à chaque classe et \(p_1, …, p_k \) les probabilités théoriques de chaque classe.
Première étape : formulation des hypothèses
\(H_0\) : « Les données observées se répartissent selon le modèle théorique spécifié, c’est-à-dire les différences entre les fréquences observées et les fréquences attendues sont simplement dues au hasard »
\(H_1\) : « Les données observées ne se répartissent pas selon le modèle théorique spécifié, c’est-à-dire les différences entre les fréquences observées et les fréquences attendues ne sont pas dues au hasard »
Deuxième étape : calcul
Calcul des effectifs théoriques : \( (n_1 + … + n_k)p_i = p_i \displaystyle \sum_{j=1}^kn_j \)
Calcul de la statistique du test : \( \displaystyle \chi ^2 = \sum_{j=1}^k \frac{(n_j – np_j)^2}{np_j} \) où \(n = \displaystyle \sum_{k=0}^nn_i \)
Calcul du degré de liberté : k – 1 (c’est-à-dire le nombre de classes \(-\)1)
Troisième étape : obtention de la valeur critique
La dernière étape de ce test est de trouver la valeur critique \( \chi^2_{\alpha} \) en fonction du nombre de degrés de liberté et du niveau de signification (notée \( \alpha\)) grâce à la table du khi-deux.
Conclusion
- Si \( \chi^2 < \chi^2_{\alpha} \), on accepte l’hypothèse \(H_0\) au niveau de signification \( \alpha \).
- Sinon, on rejette l’hypothèse \(H_0\) au niveau de signification \( \alpha\).
Exemple d’application du test d’ajustement du khi-deux
Il est désormais important de mettre en application ce test d’ajustement, car la difficulté principale de cette notion est son utilisation sur un cas concret. Nous allons donc imaginer un cas fictif qui nous permettra de mettre en œuvre ce procédé, où nous utiliserons un niveau de signification de 0,05.
Dans une étude réalisée auprès d’élèves de l’ESCP, de l’ESSEC et de NEOMA, on considère l’école comme une variable importante de l’étude. Nous prélevons un échantillon de 800 élèves qui ont répondu à l’étude et nous voulons nous assurer que cet échantillon est représentatif des élèves de ces écoles.
Nous savons que parmi l’ensemble des élèves de ces trois écoles, les élèves de l’ESCP, l’ESSEC et de NEOMA représentent respectivement 27 %, 28 % et 45 %. De plus, le nombre d’élèves par école appartenant à l’échantillon des 800 élèves est respectivement de 212, 246 et 342.
Première étape : formulation des hypothèses
\(H_0\) : « L’échantillon est représentatif de la population quant à son école »
\(H_1\) : « L’échantillon n’est pas représentatif de la population quant à son école »
Deuxième étape : calcul
Les effectifs théoriques respectivement associés à l’ESCP, l’ESSEC et à NEOMA : \( 0,27 \times 800 = 216,\) \(0,28 \times 800 = 224\) et \( \; 0,45 \times 800 = 360 \)
La statistique du test vaut \( \chi^2=\displaystyle \frac{(212-216)^2}{216}+\frac{(246-224)^2}{224}+\frac{(342-360)^2}{360} = 3,13 \)
Le degré de liberté vaut ici \( 3-1 = 2 \)
Troisième étape :
déterminer \( \chi^2_{0,05}\)
En utilisant la table du khi-deux tout en prenant en considération le nombre de degrés de liberté (ici, 2) et le niveau de signification (ici, 0,05), on trouve que \( \chi^2_{0,05} = 5,99 \)
Finalement, nous pouvons observer que \( \chi^2 < \chi^2_{0,05} \) , donc nous acceptons l’hypothèse \(H_0\) (avec un niveau de signification de 0,05).
Conclusion
En résumé, le test d’ajustement du khi-deux te permet de mettre en application tes connaissances en statistiques et en probabilité pour déterminer si une distribution théorique d’un caractère correspond à une distribution observée. Ainsi, bien que cette notion soit hors programme, son étude approfondie enrichira ta préparation aux épreuves parisiennes, notamment aux maths II !
Tu peux d’ailleurs t’entraîner sur des sujets (mathématiques approfondies) de concours abordant la loi du khi-deux (Maths I 2016 et Maths II 1999) et sur des sujets abordant les statistiques (Maths II 2012 et Maths II 2014).