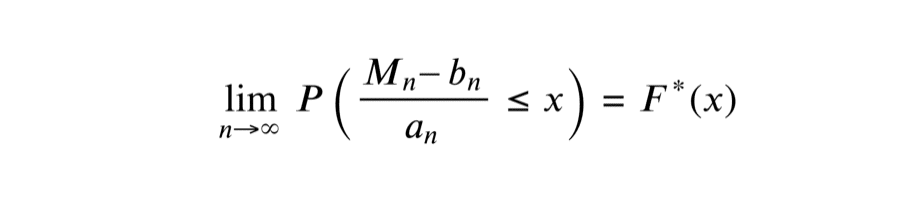Le théorème de Fisher-Tippett-Gnedenko est une pierre angulaire de la théorie des valeurs extrêmes. Il s’agit d’une branche des mathématiques qui étudie les événements rares et les valeurs maximales ou minimales d’un ensemble de données. Formulé initialement par Fisher et Tippett en 1928 et généralisé par Gnedenko en 1943, ce théorème fournit un cadre théorique pour comprendre la distribution limite des valeurs extrêmes sous certaines conditions. Cet article a pour but de présenter des notions et des propriétés hors programme, mais utiles pour les candidats qui présenteront les épreuves parisiennes (notamment Maths II) et les oraux de mathématiques.
Le théorème expliqué en français
Le théorème de Fisher-Tippett-Gnedenko énonce que si \(X_1, X_2, …, X_n\) sont des variables aléatoires indépendantes et identiquement distribuées (i.i.d.) avec une fonction de distribution \(F\), alors la distribution normalisée des maxima (ou minima) de ces variables converge en loi nécessairement vers l’une des trois distributions limites possibles :
- Distribution de Gumbel, \( \displaystyle F_{\text{Gumbel}}(x) = \exp(-\exp(-x))\), pour les distributions à queue légère.
- Distribution de Fréchet, \( \displaystyle F_{\text{Fréchet}}(x) = \exp(-x^{-\alpha})\) pour \(x > 0\), avec \(\alpha > 0\), pour les distributions à queue lourde.
- Distribution de Weibull, \( \displaystyle F_{\text{Weibull}}(x) = \exp(-(-x)^\alpha)\) pour \(x > 0\), avec \(\alpha > 0\), pour les distributions à support fini.
Ce résultat est crucial pour la modélisation des événements extrêmes, car il permet de déterminer quelle forme prend la distribution des valeurs extrêmes pour un grand nombre d’échantillons.
Applications pratiques
Le théorème trouve son application dans divers domaines tels que la météorologie, la finance et l’ingénierie civile, où il est essentiel de prédire la probabilité d’événements extrêmes.
Par exemple, dans le domaine des assurances ou de la gestion des risques naturels, connaître la distribution des événements extrêmes permet de mieux se préparer aux risques potentiels.
Formalisation du théorème
Soit \(X_1, X_2, \ldots, X_n, \) une séquence de variables aléatoires indépendantes et identiquement distribuées (i.i.d.) avec \(M_n = \max(X_1, \ldots, X_n)\) comme la valeur maximale observée. Le théorème établit que si une séquence de paires de nombres réels \((a_n, b_n)\) existe telle que \(a_n > 0\) et la limite \( \displaystyle \lim_{n \to \infty} P\left(\frac{M_n – b_n}{a_n} \leq x\right) = F^*(x) \) est une fonction de distribution non dégénérée, alors cette distribution limite \(F^*\) est l’une des trois distributions dites de valeurs extrêmes : Gumbel, Fréchet, ou Weibull. Ces trois familles de distributions sont souvent regroupées sous l’appellation de lois d’extremum généralisées.
Rappel : une fonction de distribution non dégénérée est une fonction de distribution probabiliste qui n’attribue pas toute la probabilité à un seul point (comme une distribution de Dirac). Ainsi, pour être considérée comme non dégénérée, une fonction de distribution \( F \) doit satisfaire au moins deux conditions :
- Elle doit être continue sur un intervalle de \( \mathbb{R} \).
- Elle doit avoir une variance strictement positive. Ce qui signifie que la probabilité est répartie sur plusieurs valeurs et n’est pas concentrée en un seul point.
Exemple illustratif
Supposons que nous voulons analyser les crues maximales annuelles d’un fleuve sur 50 ans.
Si \(M_n = \max(X_1, X_2, …, X_n)\) représente la crue maximale observée en une année, et si les crues suivent une distribution i.i.d., alors selon le théorème de Fisher-Tippett-Gnedenko, la distribution de \(M_n\) normalisée (par une certaine transformation linéaire \(a_nM_n + b_n\)) convergera vers l’une des trois distributions limites mentionnées ci-dessus.
Pour déterminer laquelle de ces distributions s’applique, il faut analyser les données historiques des crues.
Supposons que l’analyse montre une convergence vers la distribution de Gumbel. Alors, la probabilité d’observer une crue de niveau \(x\) ou plus est donnée par \( \displaystyle P(M_n \geq x) = 1 – \exp(-\exp(-(x – \mu)/\beta))\), où \(\mu\) et \(\beta\) sont des paramètres de localisation et d’échelle, respectivement, estimés à partir des données.
Conclusion
Le théorème de Fisher-Tippett-Gnedenko joue un rôle crucial dans notre compréhension des événements extrêmes et leur modélisation. Il ne se limite pas à une application théorique, mais s’étend à des applications pratiques significatives dans la gestion des risques et la planification à long terme.
Pour les étudiants qui préparent les épreuves parisiennes, saisir la portée de ce théorème enrichit non seulement leur bagage pour résoudre des problèmes de probabilités complexes, mais aussi leur capacité à appliquer ces connaissances dans des contextes réels et variés.
Ainsi, bien que cette notion soit hors programme, une compréhension approfondie des propriétés ci-dessus te permettra de maîtriser l’épreuve Maths II qui porte presque systématiquement sur les probabilités.
Pour t’entraîner sur ces notions de probabilités, tu peux faire ces deux sujets :
- Maths II 2010 (mathématiques appliquées)
- Maths ECRICOME 2017 (mathématiques approfondies)
Tu peux retrouver ici toutes nos autres ressources mathématiques !