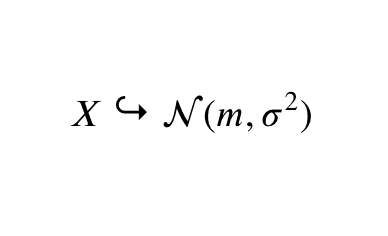Les probabilités ont une place centrale dans les programmes des prépas économiques. En effet, toutes les écoles proposent chaque année au moins un exercice mobilisant cette notion, en particulier les Parisiennes qui y consacrent une épreuve entière (la fameuse Maths II). Tu dois alors être au point sur les classiques de ce sujet et la loi normale en fait partie ! Tu vas pouvoir être certain(e) de ne rien oublier grâce à cet article.
Présentation de la loi normale
Bien qu’appelée « normale », cette loi est la plus stupéfiante. On définit la loi normale grâce à deux paramètres qui sont sa variance et son espérance. Communément, on note son espérance \(m\) et sa variance \(\sigma^2\). Ainsi, si X suit une loi normale, on note \(X \hookrightarrow\mathcal{N}(m,\sigma^2)\).
Comment savoir qu’une variable aléatoire suit une loi normale ? Cette loi se caractérise principalement par sa densité (étonnant pour une variable à densité, non ?).
Dans le cas global (où \(X \hookrightarrow\mathcal{N}(m,\sigma^2))\), une densité de X est donnée par :
\[ \displaystyle\forall x \in \mathbb{R}, f(x)=\frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{(x-m)^2}{2\sigma^2}\right)\]
Pour ta culture mathématique, il est impossible (enfin cela n’a toujours pas été fait) de trouver une primitive de \(f\). C’est pourquoi on admet dans le programme de maths que \(\displaystyle \int_{-\infty}^{+\infty} f(t) \, \mathrm{d}t=1\).
Tu connais donc la densité d’une variable suivant une loi normale. Pour la fonction de répartition, il suffit d’appliquer la définition, car pour la loi normale, il n’y a pas d’écriture explicite comme pour les autres lois usuelles.
Ainsi, on a : \(\forall x \in \mathbb{R}, F(x) = P(X\le x) =\displaystyle \int_{-\infty}^{x} f(t) \,\mathrm{d}t\).
La loi normale centrée réduite
Une variable centrée réduite est par définition une variable dont l’espérance est nulle et dont la variance vaut 1. Ainsi, si X suit une loi normale centrée réduite, elle respecte ces conditions. On note alors \(X \hookrightarrow\mathcal{N}(0,1)\).
En substituant avec les valeurs de l’espérance et la variance de X, tu obtiens sa densité qui est :
\[ \displaystyle\forall x \in \mathbb{R}, f(x)=\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{x^2}{2}\right)\]
La chose remarquable, et que tu ne devras jamais oublier lorsque tu travailles avec une telle loi, est que sa densité est paire.
Si tu as oublié comment le démontrer, voici une rapide démonstration des valeurs de l’espérance et de la variance d’une telle variable.
Démonstration de la valeur de l’espérance
Par définition, comme on sait que X admet une espérance et que X est à densité, l’espérance de X, notée E(X), vaut \(\displaystyle \int_{-\infty}^{+\infty} tf(t) \, \mathrm{d}t\). La première chose que tu dois remarquer est que la fonction intégrée est ici impaire (je te laisse lire cet article si tu doutes de la méthode pour étudier de la parité d’une fonction) par produit d’une fonction paire et d’une fonction impaire. Tu peux alors montrer que \(\displaystyle \int_{0}^{+\infty} tf(t) \, \mathrm{d}t\) converge et en déduire que l’intégrale est nulle.
Or, par croissances comparées, tu peux voir que \(\lim \limits_{t \to +\infty} t^2t\exp(-\frac{t^2}{2})\) = 0 (n’hésite pas à aller voir cet article pour être certain(e) de bien savoir étudier la convergence d’une intégrale). Or, comme tu le sais bien, \(\displaystyle \int_{1}^{+\infty} \frac{1}{t^2}\, \mathrm{d}t\) converge comme intégrale de Riemann avec \( 2 > 1\). De plus, f est une densité, donc positive sur \(\mathbb{R}\), et dans le cas d’une loi normale, \(f\) est continue sur \(\mathbb{R}\) alors, d’après le théorème de comparaison sur les fonctions continues et positives, \(\displaystyle \int_{1}^{+\infty} tf(t) \, \mathrm{d}t\) converge.
D’autre part, la fonction \(tf(t)\) est continue sur \(\mathbb{R}\), donc sur le segment \([0,1]\), ainsi l’intégrale \(\displaystyle \int_{0}^{1} tf(t) \, \mathrm{d}t\) converge comme intégrale d’une fonction continue sur un segment.
Par Chasles, tu confirmes que l’intégrale \(\displaystyle \int_{0}^{+\infty} tf(t) \, \mathrm{d}t\) comme somme d’intégrales convergentes. Comme tu as déjà évoqué l’imparité de la fonction \(t\mapsto tf(t)\), tu peux alors finalement conclure que \(\displaystyle \int_{-\infty}^{+\infty} tf(t) \, \mathrm{d}t\) vaut bien 0.
Ainsi, tu sais démontrer que E(X) = 0.
Démonstration de la valeur de la variance
Comme E(X) = 0, tu sais grâce à la formule de König-Huygens que V(X) = E(\(X^2\)). Montrons alors que \(\displaystyle \int_{-\infty}^{+\infty} t^2f(t) \, \mathrm{d}t\) converge et vaut 1. Comme précédemment, tu peux déjà remarquer que la fonction intégrée est paire par produit de fonctions paires, donc il te suffit de montrer que \(\displaystyle \int_{0}^{+\infty} t^2f(t) \, \mathrm{d}t\) converge. Tu poses alors un réel A \(> 0\) et tu réalises une intégration par parties dans l’intégrale \(\frac{1}{\sqrt{2\pi}}\displaystyle \int_{0}^{A} t^2\exp\left(-\frac{x^2}{2}\right) \, \mathrm{d}t\) (par linéarité de l’intégrale).
On pose : \[u\prime(t) = t\exp(\left(-\frac{t^2}{2}\right) \qquad u(t) = -exp(\left(-\frac{t^2}{2}\right)\]
et \[v(t) = t \qquad v\prime(t) = 1\]
Comme \(u\) et \(v\) sont des fonctions de classe \(C^1\) sur \(\mathbb{R}\), par intégration par parties et par linéarité de l’intégrale, il vient :
\(\begin{align}\frac{1}{\sqrt{2\pi}} \displaystyle \int_{0}^{A} t^2\exp\left(-\frac{t^2}{2}\right) \, \mathrm{d}t &=\frac{1}{\sqrt{2\pi}}(\big[-t\exp(\left(-\frac{t^2}{2}\right))\big]^A_0 + \displaystyle \int_{0}^{A} \exp\left(-\frac{t^2}{2}\right))\\&=-\frac{1}{\sqrt{2\pi}}A\exp\left(-\frac{A^2}{2}\right)+ 0 + \frac{1}{\sqrt{2\pi}}\displaystyle \int_{0}^{A} \exp\left(-\frac{t^2}{2}\right) \, \mathrm{d}t\end{align}\)
Tu reconnais alors la densité de X dans l’intégrale du membre de droite, et par parité de la densité de la loi normale centrée réduite, tu obtiens en faisant tendre A vers \(+\infty\) :
\[\frac{1}{\sqrt{2\pi}}\displaystyle \int_{0}^{+\infty} \exp\left(-\frac{t^2}{2}\right) \, \mathrm{d}t = \frac{1}{2}\]
Tu obtiens enfin par croissances comparées :
\[\frac{1}{\sqrt{2\pi}} \displaystyle \int_{0}^{+\infty} t^2\exp\left(-\frac{t^2}{2}\right) \, \mathrm{d}t = \frac{1}{2}\].
N’oublie pas finalement que grâce à cela, tu as prouvé l’existence de E(\(X^2\)) et donc de V(X) grâce à la parité de la fonction intégrée initialement et que celle-ci vaut :
\[V(X) = 2\frac{1}{\sqrt{2\pi}} \displaystyle \int_{0}^{+\infty} t^2\exp\left(-\frac{t^2}{2}\right) \, \mathrm{d}t = 2 • \frac{1}{2}\ = 1.\]
Propriétés principales de la fonction de répartition de la loi normale centrée réduite
Comme déjà évoqué, la densité de la loi normale est paire (ici notée \(f\)). De cette propriété en découle une autre, et celle-ci concerne sa fonction de répartition.
On note habituellement la fonction de répartition d’une telle loi \(x \mapsto \Phi(x) = P(X\le x)\). Une propriété essentielle que tu te dois de retenir en probabilité est celle-ci :
\[\fbox{\(\forall x \in \mathbb{R}, \Phi(-x) = 1 – \Phi(x)\)}\]
Pour démontrer cela, il te suffit de repartir de la définition de la fonction de répartition. (Toutes les intégrales manipulées ici sont bien convergentes, assure-toi que c’est toujours le cas avant de manipuler des intégrales.)
\(\forall x \in \mathbb{R}, \Phi(-x) = \displaystyle \int_{-\infty}^{-x} f(t) \, \mathrm{d}t\)
Tu peux alors appliquer la relation de Chasles, ce qui te donne :
\(\begin{align}\Phi(-x) = \displaystyle \int_{-\infty}^{+\infty} f(t) \, \mathrm{d}t – \displaystyle \int_{-x}^{+\infty} f(t) \, \mathrm{d}t = 1 – \displaystyle \int_{-\infty}^{x} f(t) \, \mathrm{d}t = 1 – \Phi(x) \end{align}\)
Le passage de la seconde à la troisième ligne s’explique par les propriétés de f qui est une densité paire. Ainsi, par un changement de variable classique \(u=-t\), tu obtiens le résultat approprié.
Conclusion
Ainsi, la loi normale est loin d’être normale, elle est même plutôt atypique ! On utilise bien souvent la loi normale centrée réduite, mais ne néglige pas la loi normale de manière générale, dont la densité a une expression assez complexe notamment. Tu peux observer que de nombreux sujets de concours font appel à cette loi de manière plus ou moins explicite, ce pourquoi tu dois être certain(e) de la maîtriser à 100 % !
Voici quelques sujets de ce genre :
Tu peux retrouver de façon plus globale toutes nos ressources de mathématiques ici !