Dans cet article, nous allons revoir ensemble la notion de point fixe. C’est un classique que tu peux retrouver dans (presque) tous les exercices d’analyse.
Définition d’un point fixe
Soit \(f\) une fonction définie et continue sur un intervalle stable \(I\). On appelle « point fixe » tout \(x \in I\) tel que \(f(x)=x\).
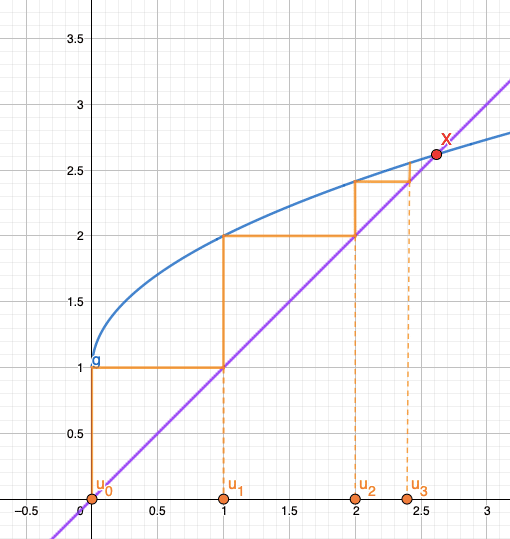
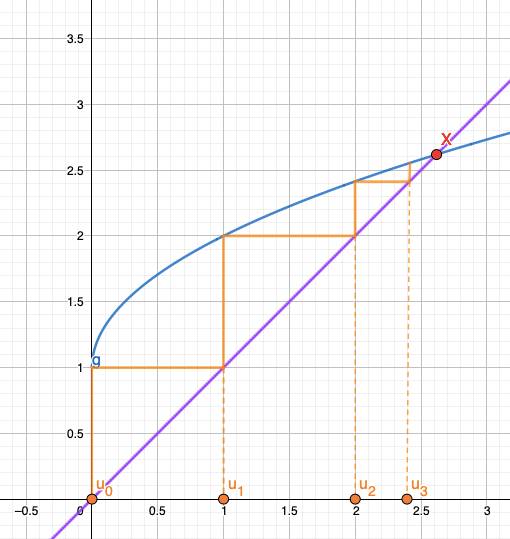
Graphiquement, il s’agit d’une intersection de la droite d’équation \(y=f(x)\) et de la droite d’équation \(y=x\).

L’étude des points fixes est la plupart du temps liée à l’étude de la suite \((u_n)_{n \in \mathbb{N}}\) définie par \(\forall n \in \mathbb{N}, u_{n+1}=f(u_n)\). Ils te permettent en effet d’obtenir des informations sur sa limite.
Il existe deux types de points fixes que nous allons étudier.
Points fixes attractifs
Les points fixes attractifs sont ceux que tu rencontres le plus souvent.
Définition
Soit \(f\) une fonction définie et continue sur un intervalle stable \(I\) et \((u_n)_{n \in \mathbb{N}}\) définie par \(\forall n \in \mathbb{N}, u_{n+1}=f(u_n)\). Soit \(x\) un point fixe de f. On dit que \(x\) est un point fixe attractif si \(\lim \limits_{n \to +\infty} u_n = x\).
Graphiquement, en construisant ta suite, tu verras apparaître cette « forme d’escargot » assez spécifique qui se resserre autour de x, ou alors une « forme d’escaliers » dont les marches deviennent plus petites à mesure qu’elles atteignent le niveau de \(f(x)\).

Montrer qu’un point fixe est une limite
La première étape est selon toute logique d’identifier les points fixes avant de t’appuyer dessus pour trouver la limite de ta suite par exemple. Pour cela, on résout l’équation \(f(x)=x\). Pour la suite, on imagine que \(\forall n in \mathbb{N}, u_n \in I\) et que \(I\) ne contient qu’un point fixe noté \(x_1\). On peut ainsi conjecturer que \((u_n)_{n \in \mathbb{N}}\) tend vers \(x_1\).
On raisonne ensuite par double implication.
Il ne faut pas oublier de montrer que si \((u_n)_{n \in \mathbb{N}}\) admet une limite, celle-ci sera nécessairement égale à \(x_1\). On s’appuie pour cela sur la propriété de continuité de la limite. En effet, si \(\lim \limits_{n \to +\infty} u_n = l\), alors \(\lim \limits_{n \to +\infty} f(u_n) = f(l)\). Donc, \(f(l)=l\). Donc, \(l\) est un point fixe.
Pour montrer l’application inverse, on s’appuie sur l’inégalité des accroissements finis. Le but est d’encadrer \(|u_n-x_1|\) pour montrer que l’expression tend vers 0. Et voilà, le tour est joué !
Points fixes répulsifs
Définition
Soit \(f\) une fonction définie et continue sur un intervalle stable \(I\) et \((u_n)_{n \in \mathbb{N}}\) définie par \(\forall n \in \mathbb{N}, u_{n+1}=f(u_n)\). Soit \(x\) un point fixe de \(f\). On dit que \(x\) est un point fixe répulsif si \(|f'(l)|>1, u_0 \ne l\) et \(\forall n \in \mathbb{N}, u_n \ne l\). Dans ce cas, \(\lim \limits_{n \to +\infty} u_n \ne x\).
Exemple :

Pour démontrer que \(\lim \limits_{n \to +\infty} u_n \ne x\), on va chercher à passer par un raisonnement par l’absurde en s’appuyant sur le théorème des accroissements finis. Je te laisse t’amuser 😉
Et c’est tout pour cet article. Tu peux maintenant jeter un coup d’œil à toutes nos autres ressources en mathématiques en cliquant juste ici.