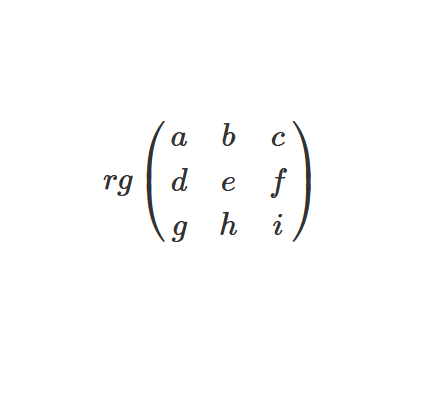Une chose est claire au regard des dernières annales (Parisiennes ou non) : calculer le rang d’une matrice est un savoir-faire essentiel. Je te propose donc ici les différentes manières de le calculer.
Calculer le rang d’une matrice
Le cas des matrices \(2 \times 2\)
Le cas des matrices \( 2\times 2\) est particulier. Il nous permet de passer par le déterminant pour trouver le rang de ces matrices. Tout repose sur quatre théorèmes.
- Théorème 1 : pour une matrice \( m \times n \), notée \( A \), le rang de la matrice, noté \(rg(A)\), est borné inférieurement et supérieurement de la sorte : \( 0 \le rg(A) \le min(m,n) \)
- Théorème 2 : on a \(rg(A)=0\) si et seulement si A est la matrice zéro \( \mathcal{O}_{m,n}
(\mathbb{R}) \) - Théorème 3 : pour une matrice \( m \times n \), notée \( A, A \) est inversible si et seulement si \(det(A) \ne 0 \)
- Théorème 4 : pour une matrice \( n \times n \), notée \( A , A \) est inversible si et seulement si \(rg(A) = n \). Attention : ceci ne concerne que les matrices carrées, et donc en particulier les matrices 2×2
Par conséquent, le rang d’une matrice \( 2\times 2\) peut être déterminé simplement en calculant son déterminant. Tu peux cliquer ici si tu veux en savoir plus sur le déterminant.
Corollaire : Une matrice de taille \( 2\times 2\), appelée \( A \), telle que \( A \ne \mathcal{O}_{2,2}
(\mathbb{R}) \), est de rang \( rg(A)=1 \) si et seulement si elle vérifie \(det(A)=0 \)
Cet enchaînement de théorème peut faire peur, mais il est en réalité très simple. Voici un schéma pour t’aider à mieux le visualiser :
Un exemple de calcul de rang d’une matrice
Prenons la matrice \(M = \begin{pmatrix} 2 & 24 \\ 4 & 48 \end{pmatrix} \)
Le rang de cette matrice est compris entre 0 et 2. Or, il est clair que cette matrice n’est pas la matrice nulle. Ainsi, son rang n’est pas 0.
De plus, on a det(\(M\)) = \( 2 \times 48 – 24 \times 4 = 96 – 96 = 0. \)
Ainsi, la matrice n’est pas inversible, et son rang n’est donc pas 2.
Conclusion : \( \fbox{\( \displaystyle rg(M) = 1 \)} \)
Le cas des matrices \(3 \times 3\)
Toutes les méthodes ci-dessous sont généralisables à n’importe quelle matrice \( M \in \mathcal{M}_{n,p} (\mathbb{R}), \text{avec} (n,p) \in \mathbb{N^2} \).
Pour des raisons de clarté, je préfère t’expliquer ici la démarche pour \( M \in \mathcal{M}_{3,3}(\mathbb{R}) \). Il suffit d’appliquer ces méthodes de la même manière à toutes les autres matrices que tu rencontreras pour déterminer le rang de ces dernières.
La méthode des systèmes
Définition 1 : le rang d’une matrice est la dimension du sous-espace vectoriel engendré par les vecteurs colonnes (ou lignes) de ladite matrice. Autrement dit, c’est le nombre maximal de vecteurs colonnes (ou lignes) linéairement indépendants.
Ainsi, pour calculer le rang, il s’agit souvent de se ramener à un système. On considère pour l’exemple la matrice \(M\) = \( \begin{pmatrix} a & b & c\\ d & e & f \\ g & h & i\end{pmatrix} \)
On a donc les colonnes suivantes : \( v_1 = \begin{pmatrix} a \\ d \\ g \end{pmatrix} , v_2 = \begin{pmatrix} b \\ e \\ h \end{pmatrix} et \; v_3 = \begin{pmatrix} c \\ f \\ i \end{pmatrix} \)
On veut effectuer un test de liberté sur cette famille de trois vecteurs. On utilise la méthode de la mise sous forme de système ici, mais d’autres méthodes sont possibles (notamment pour les matrices 1×1 ou 2×2, je te laisse cliquer ici pour voir d’autres méthodes visant à montrer la liberté ou le caractère lié d’une famille de vecteurs).
On a donc :
Soient (\( \beta, \mu, \lambda) \in \mathbb{R} \), on part de l’égalité suivante : \( \beta \times v_1 + \mu \times v_2 + \lambda\times v_3 = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} \)
À présent, si ce système implique \( \beta = 0, \ \mu = 0 \ et \ \lambda = 0 \), alors \(rg(M) = 3\), car les trois vecteurs v1, v2 et v3 sont linéairement indépendants (car la famille est libre). Au contraire, s’il existe une combinaison linéaire et que l’un des vecteurs est le même (à constante multiplicative près) que l’un des deux autres vecteurs, alors \( rg(M) = 2 \), et si deux des vecteurs sont linéairement dépendants d’un autre, alors \(rg(M) = 1. \)
Nous avons d’ailleurs vu (voir au-dessus) que dans ce cas, le rang de \(M\) ne peut pas être égal à 0.
Un exemple de calcul de rang de matrice
Prenons un exemple concret avec la matrice \(A\) = \( \begin{pmatrix} 4 & -3 & 7\\ -1 & 6 & 3 \\ 2 & 9 & 13\end{pmatrix} \)
Soient (\( \beta, \mu, \lambda) \in \mathbb{R^3} \), on a le test de liberté suivant :
\( \begin{cases} \begin{align} & 4\beta -3\mu +7\lambda = 0 \\& -\beta +6\mu +3\lambda = 0 \\& 2\beta +9\mu +13\lambda = 0 \end{align}\end{cases} \) \( \Rightarrow \begin{cases} \begin{align} & 4\beta -3\mu +7\lambda = 0 \\& \ \ \ \ +21\mu +19\lambda = 0 \\& \ \ \ \ +21\mu +19\lambda = 0 \end{align} \end{cases} \)
(on a fait \( \scriptsize{L2 <– 4L2 + L1 \ et \ L3 <– 2L3 – L1} \))
\( \\\) On remarque que L2=L3. Donc, il nous reste : \( \begin{cases} \begin{align} 4\beta -3\mu +7\lambda = 0 \\ \ \ \ \ \ 21\mu +19\lambda = 0 \end{align} \end{cases} \Rightarrow \begin{pmatrix} \beta = \frac{-17}{7}\lambda \\ \mu = \frac{-19}{21}\lambda \\ \lambda=\lambda \end{pmatrix} \)
Ainsi, il y a ici deux vecteurs colonnes linéairement indépendants, et donc d’après la définition 2, on a que : \( \fbox{\( \displaystyle rg(M) = 2 \)} \)
Ceci, encore une fois, est généralisable à n’importe quelle matrice \( M \in \mathcal{M}_{m,n} \). Le rang sera \( rg(M) = n-x \), avec \(x \ \) le nombre de vecteurs linéairement dépendants à un autre vecteur.
La méthode de l’échelonnement par trouver le rang d’une matrice de façon astucieuse
Cette méthode est en réalité semblable à celle du pivot de Gauss. Elle peut être plus rapide, mais nécessite de la rigueur dans l’application. Une matrice \(M\) est dite échelonnée si :
- chaque ligne non nulle de \(M\) commence avec strictement plus de 0 (c’est-à-dire, 1 ou plus) que la ligne précédente ;
- les lignes nulles (ne contenant que des 0) de \(M\) viennent en bas après les lignes non nulles.
Définition 2 : le rang d’une matrice \(M\) est le nombre de lignes (ou colonnes) non nulles dans sa forme échelonnée en ligne (ou colonnes).
On cherche donc à effectuer des combinaisons linéaires sur les colonnes (ou lignes) de \(M\), puisque ces opérations ne modifient pas le rang de \(M\).
Un exemple
Soit \(M\) = \( \begin{pmatrix} 1 & 3 & 2\\ 1 & 4 & 1 \\ 0 & 1 & -1\end{pmatrix} \)
Alors : \( rg(M) = rg\begin{pmatrix} 1 & 3 & 2\\ 1 & 4 & 1 \\ 0 & 1 & -1\end{pmatrix} = rg\begin{pmatrix} 1 & 3 & 2\\ 0 & 1 & -1 \\ 0 & 1 & -1\end{pmatrix} = rg\begin{pmatrix} 1 & 3 & 2\\ 0 & 1 & -1 \\ 0 & 0 & 0\end{pmatrix} = \fbox{\( \displaystyle 2 \)} \)
En passant par le noyau
Soit \((m,n) \in \mathbb{N^2} \), Soit \( \ M \in \mathcal{M}_{m,n}(\mathbb{R}) \)
Mathématiquement parlant, une matrice est une application linéaire et on peut donc appliquer le théorème du rang, qui nous donne l’égalité suivante :
\[
\begin{align}
& dim(\text{Ker}(M)) + rg(M) = n, \scriptsize{\text {avec n qui est donc le nombre de colonnes de} \ M} \\
& \Leftrightarrow rg(M) = n \ – \ dim(\text{Ker}(M))
\end{align}
\]
Ainsi, si tu as déjà calculé \( Ker(M) \) lors d’une précédente question, tu peux en déduire le rang de \(M\).
Un exemple
Soit \( (x_1, x_2, x_3) \in \mathbb{R^3} \)
Soit \(M = \left(\begin{array}{cccccc}1&2&1\\2&3&2\\1&1&1\end{array}\right) \)
On se propose de déterminer son noyau. Il suffit de résoudre l’équation matricielle :
\[ \left(\begin{array}{cccccc}1&2&1\\2&3&2\\1&1&1\end{array}\right)\left(\begin{array}{cccccc}x_1\\x_2\\x_3\end{array}\right)=\left(\begin{array}{cccccc}0\\0\\0\end{array}\right) \]
Ce qui est équivalent au système :
\[ (\mathcal S_1)\quad\left\{\begin{array}{ccccccccc}x_1&+&2x_2&+&x_3&=&0\\2x_1&+&3x_2&+&2x_3&=&0\\x_1&+&x_2&+&x_3&=&0\end{array}\right. \]
\[\Leftrightarrow (\mathcal S_2)\quad\left\{\begin{array}{ccccccccc}x_1 \ + &2x_2 \ + &x_3&=&0 \\ & x_2 & &=&0\end{array}\right. \]
\[\Leftrightarrow (\mathcal S_3)\quad\left\{\begin{array}{rcl}x_1 &=& -x_3 \\ x_2 &=& 0\end{array}\right. \]
Ainsi, \( ker(M) \ \)= \( Vect\begin{pmatrix} -1 \\ 0 \\ 1 \end{pmatrix} \)
Et puisque \( \begin{pmatrix} -1 \\ 0 \\ 1 \end{pmatrix} \ne \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} \), d’après le cours, on a que \( dim(ker(M)) = 1. \)
Ainsi, d’après l’égalité donnée par le théorème du rang, \( \fbox{\( \displaystyle rg(M) = 3 \ – 1 = 2 \)} \)
Conclusion
Tu connais maintenant toutes les méthodes pour calculer le rang d’une matrice. Cela te permettra d’aller plus vite pour répondre aux différentes questions dans tes DS.
Je te conseille d’essayer de garder en tête les questions précédentes. Cela t’aidera à détecter plus facilement laquelle de ces méthodes tu dois d’utiliser.
Tu peux retrouver ici toutes nos autres ressources mathématiques.