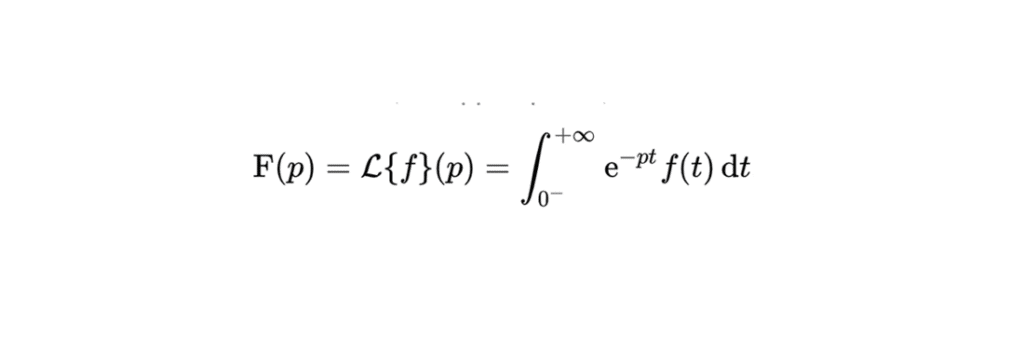La transformée de Laplace est une notion centrale d’analyse liée au calcul d’intégrales et à la résolution d’équations différentielles. Elle est d’ailleurs déjà tombée au concours. Dans cet article, il sera question de la définition de cette transformée, de ses propriétés ainsi que de quelques exemples d’application de la notion.
Introduction
La transformée de Laplace tient son nom du mathématicien français Simon Laplace. Elle désigne une transformation intégrale qui, à une fonction \(f\) intégrale définie sur les réels positifs et à valeurs dans \(\mathbb{R}\), associe une fonction \(F\) définie sur les complexes et à valeurs complexes.
Attention, puisque les complexes sont hors programme depuis la réforme des prépas ECG, nous nous intéresserons seulement aux transformées de Laplace de \(\mathbb{R}\) dans \(\mathbb{R}\).
Portée de la notion
La transformation de Laplace est très utile dans la résolution d’équations différentielles. Il suffit en effet de transposer l’équation différentielle dans le domaine de Laplace pour obtenir une équation beaucoup plus simple à manipuler. En effet, à partir de la transformée \(F\), il est possible de retrouver la fonction \(f\) d’origine, c’est-à-dire qu’il existe une expression de \(f\) en fonction de \(F\), que nous verrons dans la suite de cet article.
Certes, la notion de résolution d’équations différentielles n’est pas vraiment dans l’esprit du programme, mais est déjà apparue dans plusieurs sujets (notamment EMLYON 2015). Il n’est donc pas inutile d’être familier avec la notion de transformation de Laplace.
Définition
Soit \(f\) une fonction définie sur \(\mathbb{R}_{+}\) tel que \(\displaystyle \int_{0}^{+\infty} e^{-pt}f(t) \,\mathrm{d}t\), \(p \in \mathbb{R}\) converge, alors on définit la fonction \(F\), appelée transformée de Laplace, par :
\[\fbox{\(F(p) =\mathcal{L}(f)(p) = \displaystyle \int_{0}^{+\infty} e^{-pt}f(t) \,\mathrm{d}t\)}\]
Attention à toujours vérifier qu’une telle intégrale existe ! Il faut en effet vérifier sa convergence, puisque l’on manipule des intégrales généralisées. On définit donc la transformée \(F\) seulement pour les valeurs de \(p\) tel que l’intégrale converge.
Propriétés
Linéarité
À l’aide de la définition précédente, il est clair que la linéarité de l’intégrale assure que la transformée de Laplace est linéaire. On a donc
\[\forall (a,b) \in \mathbb{R}^2 , \mathcal{L}(af +bg) = a\mathcal{L}(f) + b\mathcal{L}(g)\]
Transformation de Laplace d’une dérivée
À l’aide d’une intégration par parties, on peut démontrer la propriété suivante :
\[\mathcal{L}(g’)(p) = p\mathcal{L}(g)(p) -\lim \limits_{t \to 0_{-} }f(t)\]
Conséquence (dérivation à l’ordre \(n\))
Plus encore, on peut généraliser la formule précédente à l’aide d’un raisonnement par récurrence. On obtient alors le résultat suivant :
\[\forall n \in \mathbb{N^{*}}, \mathcal{L}(g^{n})(p) = p^n\mathcal{L}(g)(p) – \displaystyle \sum_{k=0}^{n-1}p^{n-1-k}\lim \limits_{t \to 0_{-} }f^{k}(t)\]
Translation temporelle
Cette propriété est bien plus utile en physique, mais il est bon de la maîtriser pour les écrits d’ECG. Soit \(t_0 >0\) et \(g(t)=f(t-t_0)\) (d’où le fait que g est bien une translation dite temporelle de \(f\)). Alors, on a la propriété suivante :
\[\mathcal{L}(g)(p) = e^{-pt_0}\mathcal{L}(f)(p)\]
La démonstration de cette propriété est assez immédiate, il suffit d’utiliser les propriétés sur les exponentielles, puis la linéarité de l’intégrale.
Théorème d’inversion de la transformée de Laplace
La transformée de Laplace est injective, c’est-à-dire qu’à partir de la fonction \(F\), il est possible de retrouver (avec plus ou moins de difficulté) la fonction \(f\) à l’origine. Cependant, cette formule appelée « formule d’inversion de Bromwitch » fait intervenir les nombres complexes et n’est donc pas du tout amenée à tomber au concours.
Comme nous l’avons déjà précisé précédemment, c’est cette propriété qui permet de résoudre plus simplement des équations différentielles. Faute de pouvoir introduire la formule d’inversion de Bromwitch, il est concevable qu’un sujet fasse appel à des cas simples où les candidats pourraient directement déterminer \(f\) à partir de \(F\).
Exemples
Cas classiques
Il existe un tableau des transformations de Laplace pour les fonctions usuelles. Inutile de l’apprendre par cœur, mais voici certaines transformations de Laplace classiques.
On a par exemple :
\(\forall a \in \mathbb{R}\), \(f(x)= e^{ax} \Rightarrow F(a) =\displaystyle \frac{1}{p-a}\)
Ou encore : \(\forall a \in \mathbb{R}, f(x)= sin(at) \Rightarrow F(a) = \displaystyle\frac{a}{p^2+a^2}\)
Pour un cas encore plus complexe, on aura :
\(\forall a \in \mathbb{R} ,\forall n \in \mathbb{N}, f(x)= t^{n}e^{at} \Rightarrow F(a) =\displaystyle \frac{n!}{(z-a)^n+1}\)
Pour démontrer de tels résultats, on aura souvent recours aux intégrations par parties et, parfois, à des récurrences où une intégration par parties sera nécessaire dans l’hérédité.
Cas plus exotiques
Toutefois, le tableau qui contient les formules usuelles ne permet pas d’appréhender toutes les fonctions. Considérons par exemple \(f : x \mapsto x^2\), dont on vérifie rapidement que \(F\) est définie sur \(\mathbb{R_{+}^{*}}\).
Pour calculer \(F(p) = \displaystyle \int_{0}^{+\infty} e^{-pt}t^2 \,\mathrm{d}t\), on a ici plusieurs possibilités.
Première possibilité : intégration par parties
On réalise deux intégrations par parties en dérivant \(t^2\), puis \(t\) afin de reconnaître une intégrale exponentielle de référence. On a donc un calcul long qui prend plus d’une page de calculs, mais qui a le mérite de donner le résultat s’il est mené sans faute de calcul. Le résultat est donc le suivant :\[\forall p \in \mathbb{R_{+}^{*}} , F(p) = \frac{2}{p^3}\]
Deuxième possibilité : recours aux probabilités
Cette manière de raisonner demande bien plus de maîtrise du cours, mais est bien plus rapide et élégante. Il suffit en fait de remarquer que l’on est presque en présence du moment d’ordre deux d’une loi exponentielle de paramètre p>0 (notons-la \(X\)). On compense alors le réel \(p\) manquant en écrivant :
\(F(p) = \frac{1}{p}\displaystyle \int_{0}^{+\infty} {p}e^{-pt}t^2 \,\mathrm{d}t\)
À l’aide de la formule de König-Huygens, on a \(E(X) = V(X) + E(X)^2 = \frac{1}{p^2} + (\frac{1}{p})^2 = \frac{2}{p^2}\)
On conclut donc que \[\forall p \in \mathbb{R_{+}^{*} }, F(p) = \frac{2}{p^3}\]
Troisième possibilité : changement de variable
On peut également poser le changement de variable affine, donc bien définie, \(u = pt\), qui donne :
\(F(p) =\displaystyle \int_{0}^{+\infty}e^{-pt}t^2 \,\mathrm{d}t = \displaystyle \int_{0}^{+\infty} \frac{1}{p}e^{-u}(\frac{u}{p})^2 \,\mathrm{d}u = \frac{1}{p^3}\Gamma(3) = \frac{1}{p^3}2! =\frac{2}{p^3}\)
Ce que montre cet exemple, c’est qu’il existe souvent plusieurs manières de procéder pour déterminer la transformée de Laplace, mais il y en a souvent une qui permet de gagner du temps !
Application à la résolution d’une équation différentielle
Posons l’équation différentielle suivante à résoudre :
\((E) : \forall t \in \mathbb{R_{+}^{*}}, f^{(2)}(t) + f'(t) = t^2\) et tel que \(f'(0) = 0\). On prend alors la transformée de Laplace de l’équation suivante et on obtient, d’après les propriétés précédentes :
\((E) : t^2F(t) + tF(t) = \frac{2}{t^3}\). Rappel : \(\frac{2}{t^3}\) a été obtenue précédemment lors de l’exemple pour les cas exotiques des transformations de Laplace.
Il suffit alors d’isoler \(F(t)\) pour obtenir :
\((E) :F(t) = \frac{2}{t^3(t^2+1)}\)
On conclut alors en utilisant le théorème d’inversion de transformation de Laplace pour passer de \(F\) à \(f\). Mais cette formule est trop largement hors programme pour être exploitée ici. C’est pourquoi, si un tel sujet tombe aux concours, tu seras toujours en face du résultat d’une intégrale de référence ! Admettons par exemple que tu te retrouves avec :
\((E’) : F(a)= \frac{1}{a^2}\). Alors, tu reconnais le résultat de cours sur l’espérance d’une loi géométrique (notons-la G) de paramètre \(a\) et tu reconnais que \(\displaystyle \int_{0}^{+\infty}ae^{-at}(t-E(G))^2 \mathrm{d}t = V(G) = \frac{1}{a^2}\) (d’après le théorème de transfert). Tu conclus alors que \(f(t) = a(t-E(G))^2 = a(t-\frac{1}{a})^2\)
On comprend avec cet exemple que ce qui peut être fait avec les outils du programme ne rime pas nécessairement avec facilité. Toujours est-il que tu comprends alors complètement l’intérêt de la transformation de Laplace !
Conclusion
En définitive, la transformation de Laplace permet de manipuler une très large partie du chapitre sur les intégrales et est donc particulièrement pertinente pour un sujet d’écrit ou d’oral. Puisque tu arrives au bout de cet article, tu peux t’entraîner sur le sujet EMLYON 2004 ou encore la Maths II 2002. Tu verras que certaines questions te seront familières ! Il n’y a désormais plus qu’à espérer que cette notion tombe le jour J !
Tu peux retrouver le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder à toutes nos autres ressources mathématiques !