Le triangle de Pascal est un incontournable de l’arithmétique, mais il est également très utile en dénombrement. Plus généralement, ce triangle, d’une grande simplicité, cache un nombre incalculable de propriétés qui servent dans différents domaines des mathématiques. Dans cet article, nous verrons l’histoire de ce triangle, sa construction, quelques propriétés très intéressantes, ses liens avec d’autres notions très connues (comme la suite de Fibonacci) et sa construction sur Python.
Histoire du triangle de Pascal
Tout d’abord, il est important de préciser que Blaise Pascal n’est pas l’inventeur dudit triangle. En effet, ce dernier avait déjà été découvert, parfois plusieurs siècles auparavant, par des mathématiciens chinois, indiens, perses, etc.
Ainsi, le nom de ce triangle n’est pas universel : en Chine, il s’appelle « triangle de Yang Hui », en Perse, il est nommé « triangle de Khayyam » et même en Italie, il est appelé différemment, puisque les Italiens le nomment « triangle de Tartaglia ».
Mais alors, pourquoi est-ce que la majorité des pays d’Occident appelle ce triangle particulier « triangle de Pascal » ? Cela s’explique par les apports du mathématicien français le concernant. En 1654, Pascal écrit Traité du triangle arithmétique, un ouvrage dans lequel il présente le triangle et 19 de ses propriétés. Mais à la différence de ses prédécesseurs, il démontre les propriétés qu’il avance, et ce, en utilisant un procédé innovateur à l’époque : le raisonnement par récurrence.
Lire aussi : L’itération : méthode (détaillée) pour apprendre à conjecturer une récurrence
Construction du triangle de Pascal
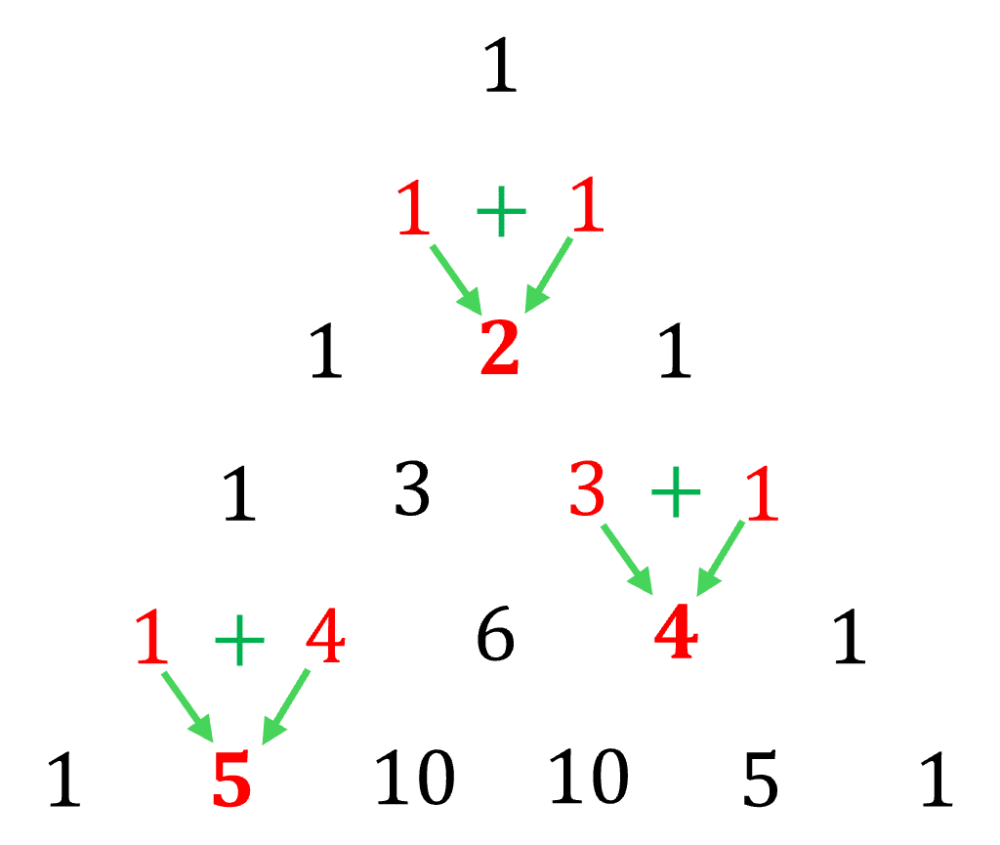
Schématiquement, le triangle de Pascal se construit assez simplement. D’abord, on place des \(1\) aux extrémités latérales du triangle. Ensuite, on additionne les deux chiffres qui se situent au-dessus du chiffre dont on cherche à calculer sa valeur, et ainsi de suite.
Par exemple, pour déterminer les valeurs de la troisième ligne (cf. schéma ci-dessous : \(1\text{ }\color{red}{2}\text{ }1\)), on procède comme suit : on connaît déjà la valeur des extrémités (qui sont des \(1\)), et pour trouver \(\color{red}{2}\), on additionne les deux chiffres du dessus, qui sont \(\color{red}{1}\) et \(\color{red}{1}\), ce qui donne bien \(\color{red}{1}\color{green}{+}\color{red}{1}\color{green}{\rightarrow}\color{red}{2}\). Ainsi, pour calculer la valeur du quatrième chiffre de la cinquième ligne (i.e. \(\color{red}{4}\)), on additionne les deux chiffres au-dessus de ce dernier, c’est-à-dire \(\color{red}{3}\) et \(\color{red}{1}\), ce qui donne bien \(\color{red}{4}\), comme on peut le voir sur le schéma ci-dessous. De même pour le dernier cas, on trouve \(\color{red}{5}\), en additionnant les chiffres qui sont au-dessus (en l’occurrence \(\color{red}{1}\) et \(\color{red}{4}\)).
Mathématiquement, le triangle se construit à l’aide de la relation de Pascal (ou la formule du triangle de Pascal) : \[\forall (n,k)\in\mathbb{N^*}^2, k\le n,{{n}\choose{k}} = {{n-1}\choose{k-1}}+{{n-1}\choose{k}}\]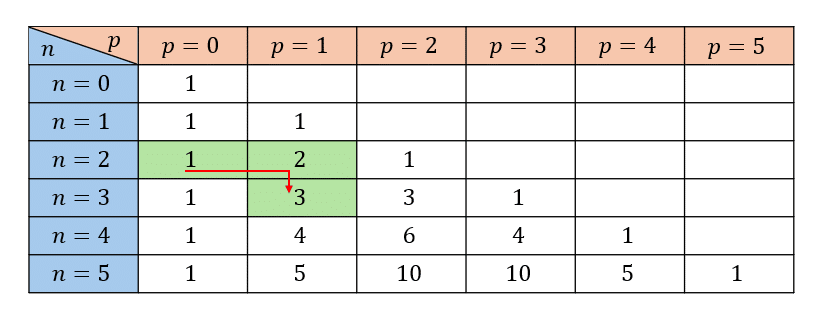
On remarque que chaque coefficient du tableau représentant le triangle de Pascal correspond à la quantité : \(\begin{align}{{n}\choose{p}}\end{align}\). Par exemple, pour le 1 sur fond vert, il correspond à \(\begin{align}{{2}\choose{0}}\end{align}\).
Finalement, ceci étant dit, on pourrait réécrire le triangle de Pascal sous la forme suivante :
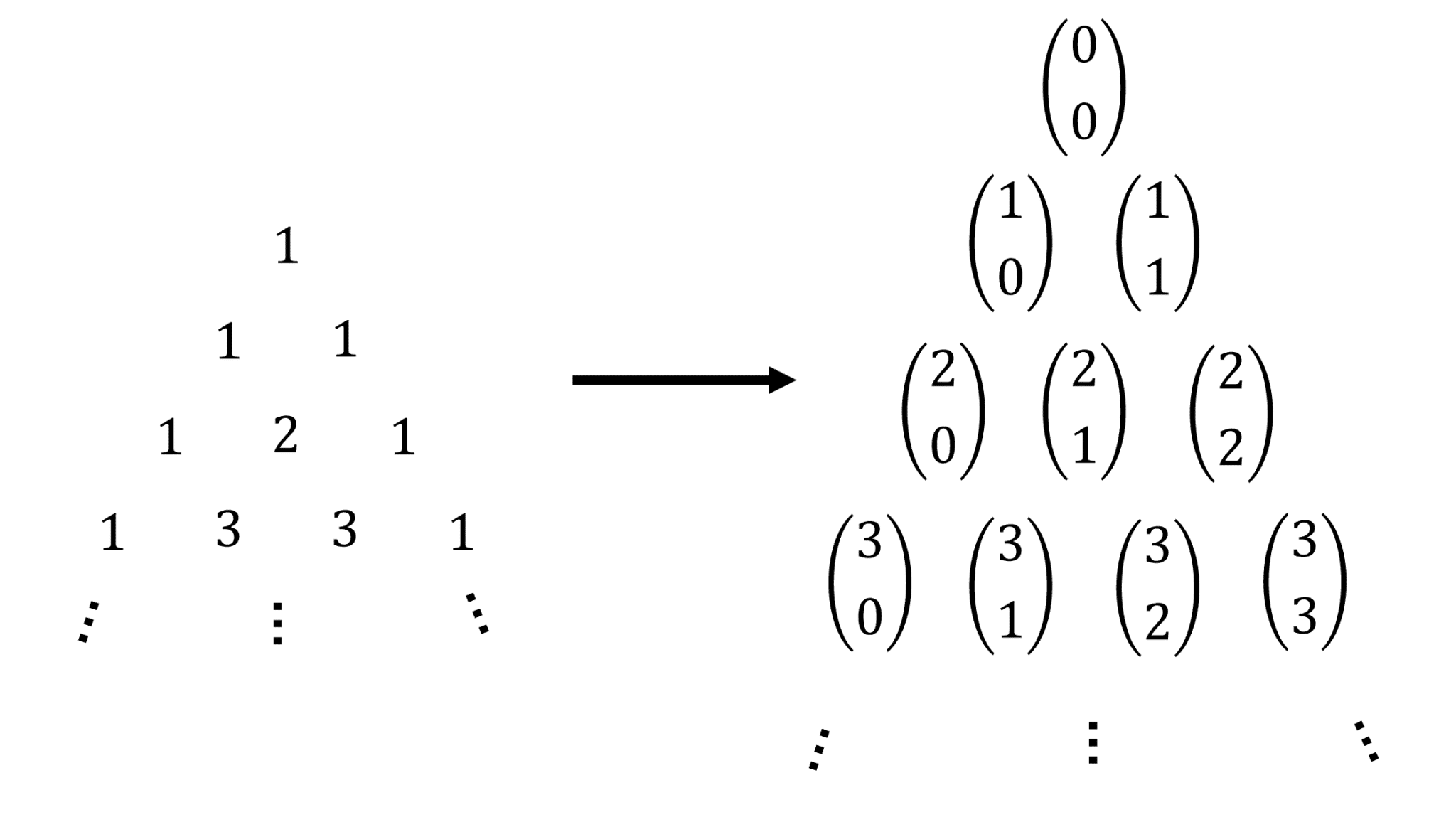
Ainsi, on remarque plus aisément que\(\begin{align} {{2}\choose{0}}+{{2}\choose{1}}={{3}\choose{1}} \end{align} \), ce qui correspond bien à la formule d’itération de Pascal.
Démonstration
Soient \(n,k\in \mathbb{N}\), tels que : \(0<k \le n\).
\(\begin{align}{{n-1}\choose{k-1}}+{{n-1}\choose{k}} &= \frac{(n-1)!}{(k-1)!(n-k)!}+\frac{(n-1)!}{k!(n-k-1)!}\\&= \frac{(n-1)!}{(k-1)!(n-k-1)!(n-k)}+\frac{(n-1)!}{k(k-1)!(n-k-1)!}\\ &= \frac{(n-1)!}{(n-k-1)!(k-1)!}\left(\frac{1}{n-k}+\frac{1}{k}\right)\\ &= \frac{(n-1)!}{(n-k-1)!(k-1)!}\frac{n}{k(n-k)}\\ &= \frac{n!}{k!(n-k)!}\\&= {{n}\choose{k}}\end{align}\)
D’où le résultat.
Maintenant que tu sais construire le triangle de Pascal, intéressons-nous à ses propriétés.
Propriétés du triangle de Pascal
Formule sommatoire avec \(2^n\)
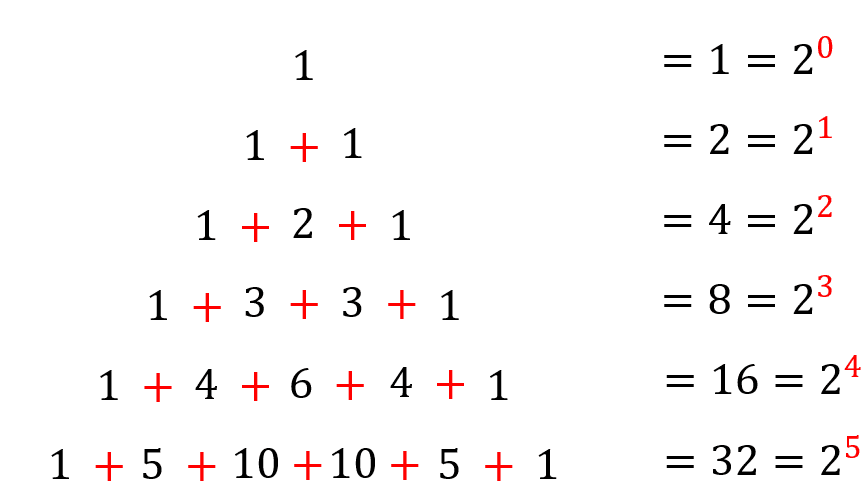
À travers le schéma ci-dessus, tu peux remarquer que lorsque l’on additionne les coefficients sur chaque ligne du triangle de Pascal, on obtient les éléments de la suite des \((2^n)_{n\in \mathbb{N}}\).
Démonstration
Compte tenu que l’on s’intéresse à chaque ligne, le numéro de la ligne est fixé. C’est pourquoi, pour la \(n^{\text{ième}}\) ligne, sa somme est décrite par la quantité : \(\sum_{p=0}^n {{n}\choose{p}}\), qui correspond, en fait, par application du binôme de Newton, a :
\(\begin{align}\sum_{p=0}^n {{n}\choose{p}} = \sum_{p=0}^n {{n}\choose{p}}1^n 1^{n-p} = 2^n\end{align}\).
D’où le résultat.
Formule sommatoire avec alternance de signe
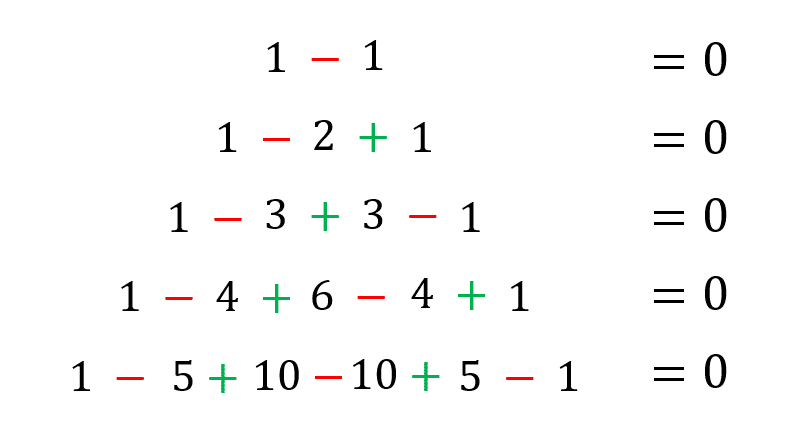
Comme le met en évidence le schéma ci-dessus, on remarque que pour \(n\ge 1\), la somme des coefficients de chaque ligne, lorsqu’on fait alterner le signe entre chaque chiffre (ou nombre), est égale à 0.
Démonstration
Si on se donne un \(n\) fixé ( \(n\ge 1\)), qui correspond à la \(n^{ième}\) ligne du triangle, on a alors alors, par la formule du binôme :
\(\begin{align}\sum_{p=0}^n {{n}\choose{p}}(-1)^p = \sum_{p=0}^n {{n}\choose{p}}(-1)^p 1^{n-p} = (1-1)^n = 0^n = 0\end{align} \)
Formule de la crosse de Hockey cachée dans le triangle de Pascal
Comme tu peux l’observer, la crosse de Hockey se forme en effectuant l’addition d’une diagonale descendante, dont la somme est égale au chiffre (ou au nombre) qui arrête la diagonale.
À titre d’exemple, prenons la deuxième diagonale descendant de la droite vers la gauche (représentée sur le schéma en rouge) : \(1\color{red}{+}2\color{red}{+}3\color{red}{+}4\color{red}{=}10\), où \(10\) est le nombre qui arrête le prolongement de la diagonale.
À noter que cette propriété reste vérifiée en prenant une diagonale qui descend de la gauche vers la droite.
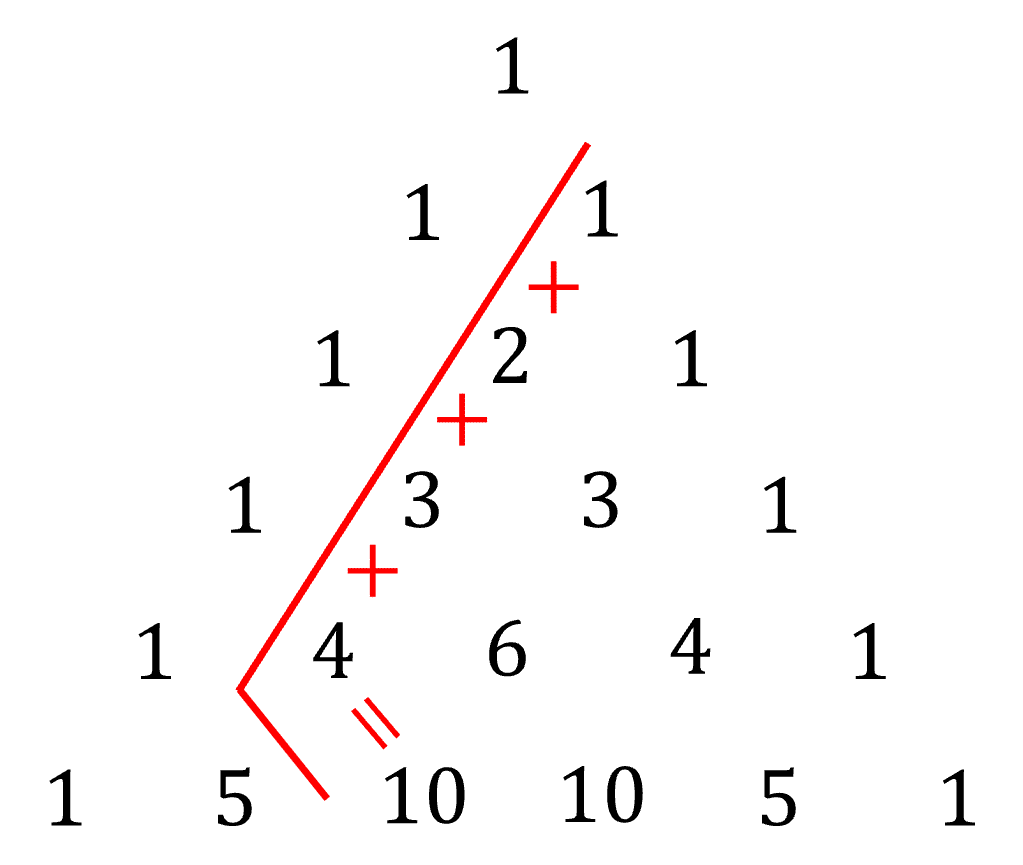
Cette situation est décrite en langage mathématique à travers la relation suivante : \[\sum_{k=p}^n{{k}\choose{p}}={{n+1}\choose{p+1}}\text{ , pour } n\ge p\ge 0\]
Démonstration
Il existe plusieurs démonstrations de cette formule (par récurrence sur \(n\), formule du binôme de Newton) dans la littérature, je vais me restreindre à celle qui suit.
Pour rappel, en utilisant la formule du triangle de Pascal, on a :
\[\begin{align} \sum_{k=p}^n{{k}\choose{p}} &= \sum_{k=p}^n\left[ {{k+1}\choose{p+1}}- {{k}\choose{p+1}}\right]\\&= {{n+1}\choose{p+1}} – {{p}\choose{p+1}}(\text{ somme télescopique})\\&={{n+1}\choose{p+1}}(\text{ car } {{p}\choose{p+1}}=0)\end{align}\]
Ce qui prouve le résultat.
Formule sommatoire des diagonales à l’intérieur du triangle de Pascal
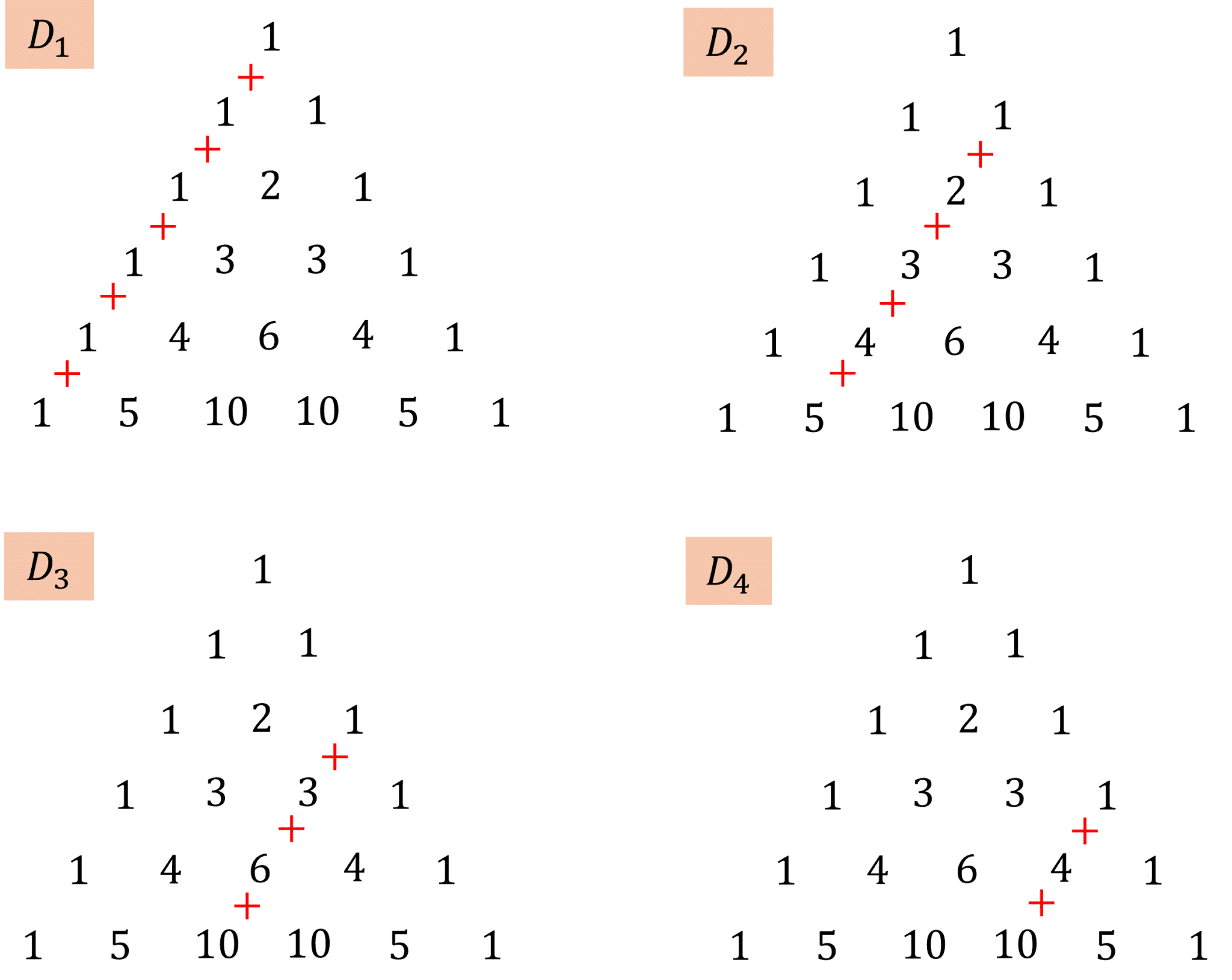
Lorsque l’on considère les quatre premières diagonales du triangle (en partant de la gauche ou de la droite ; cela revient au même du fait de la symétrie du triangle), on constate que ces dernières suivent des patterns très particuliers.
Pour la première diagonale \(D_1\), on constate que c’est une suite de 1.
En ce qui concerne la deuxième diagonale \(D_2\), on remarque qu’elle donne tous les entiers de \(\mathbb{N^*}\).
La troisième diagonale \(D_3\) est un peu plus particulière : la suite de nombres correspond aux nombres triangulaires, qui sont les nombres qui permettent de construire un triangle isocèle à l’aide de boules :
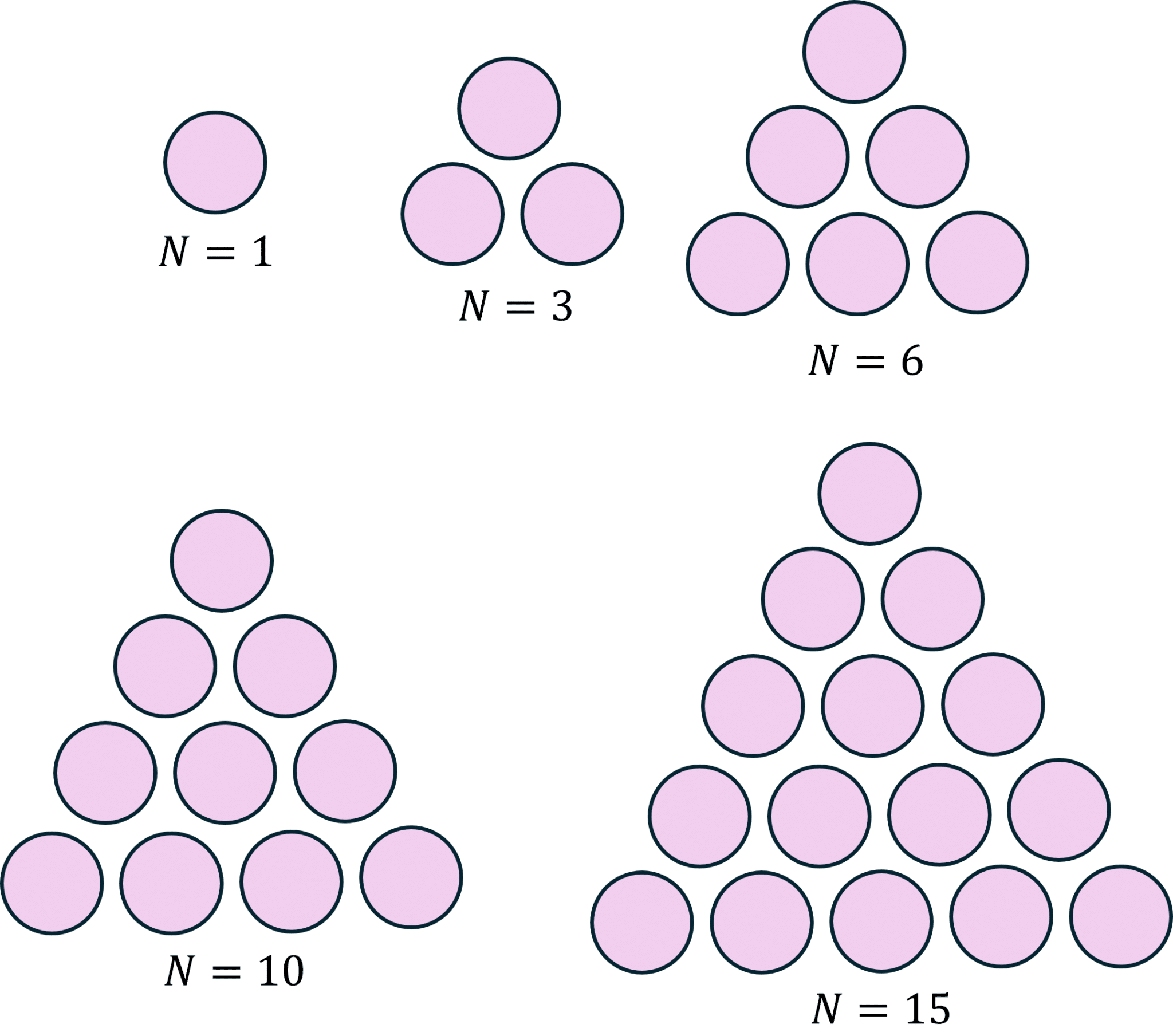
Enfin, la quatrième diagonale \(D_4\) nous donne l’ensemble des nombres tétraédriques, c’est-à-dire les nombres qui permettent de construire des tétraèdres avec des boules ; c’est comme pour \(D_3\), mais cette fois-ci avec des triangles à trois dimensions.
Formule sommatoire avec \(11^n\)
Précédemment, on a constaté qu’à chaque ligne, il se cachait un \(2^n\). Or, un autre nombre à la puissance \(n\) se cache également : \(11^n\).
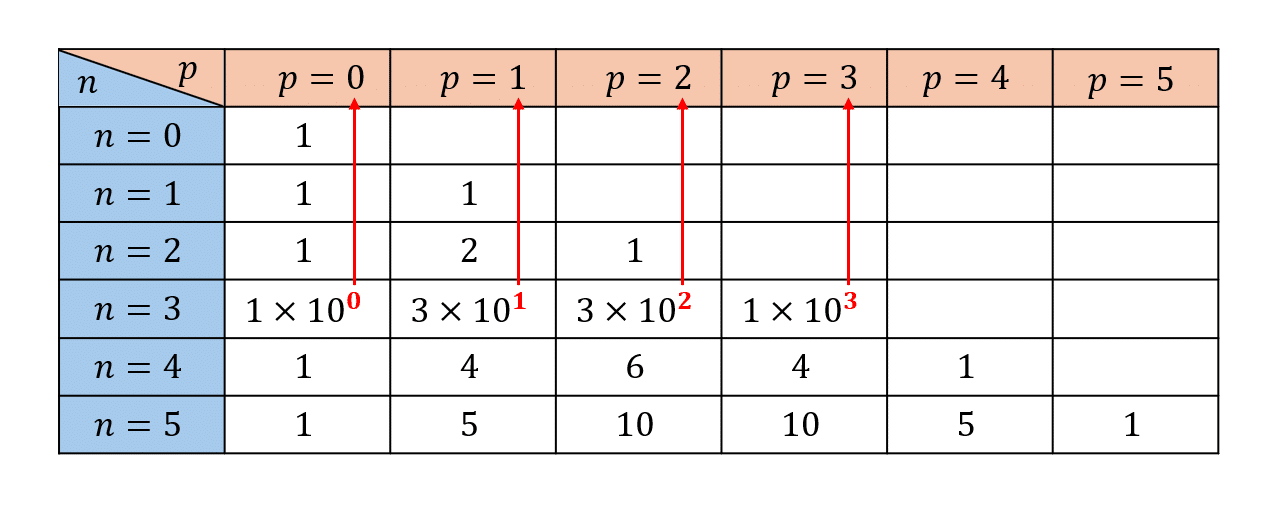
Comment le débusquer ? C’est relativement simple, il suffit de multiplier chaque coefficient d’une ligne par \(10^p\), puis de sommer tous les coefficients de la ligne. Où \(p\) est la colonne dans laquelle se situe le \(p^{ième}\) coefficient, comme on peut l’observer dans le tableau ci-dessous.
En guise d’exemple, prenons la quatrième ligne du tableau \((i.e. n=3)\), on a : \(1 \times 10^{\color{red}{0}}+3\times\ 10^{\color{red}{1}}+3\times 10^{\color{red}{2}}+1\times 10^{\color{red}{3}}=1331=11^3.\)
De façon analogue, on obtient pour \(n=2\) : \(1 \times 10^{\color{red}{0}}+2\times\ 10^{\color{red}{1}}+1\times 10^{\color{red}{2}}=121=11^2,\) etc.
Démonstration
Comme pour les démonstrations précédentes, elle repose sur le binôme de Newton. En effet, pour chaque ligne, on fait la somme des coefficients, chacun multiplié par \(10^p\). Ce qui donne en langage mathématique : \(\sum_{p=0}^n {{n}\choose{p}}10^p.\)
Par application du binôme de Newton, on a : \(\begin{align}\sum_{p=0}^n {{n}\choose{p}}10^p = \sum_{p=0}^n {{n}\choose{p}}10^p 1^{n-p}=(10+1)^n=11^n\end{align}.\)
D’où le résultat.
Formule du produit des coefficients alternés autour d’un coefficient en particulier
Derrière ce nom de propriété assez barbare se cache une propriété assez surprenante, qu’une image saura mieux expliquer que mille mots :
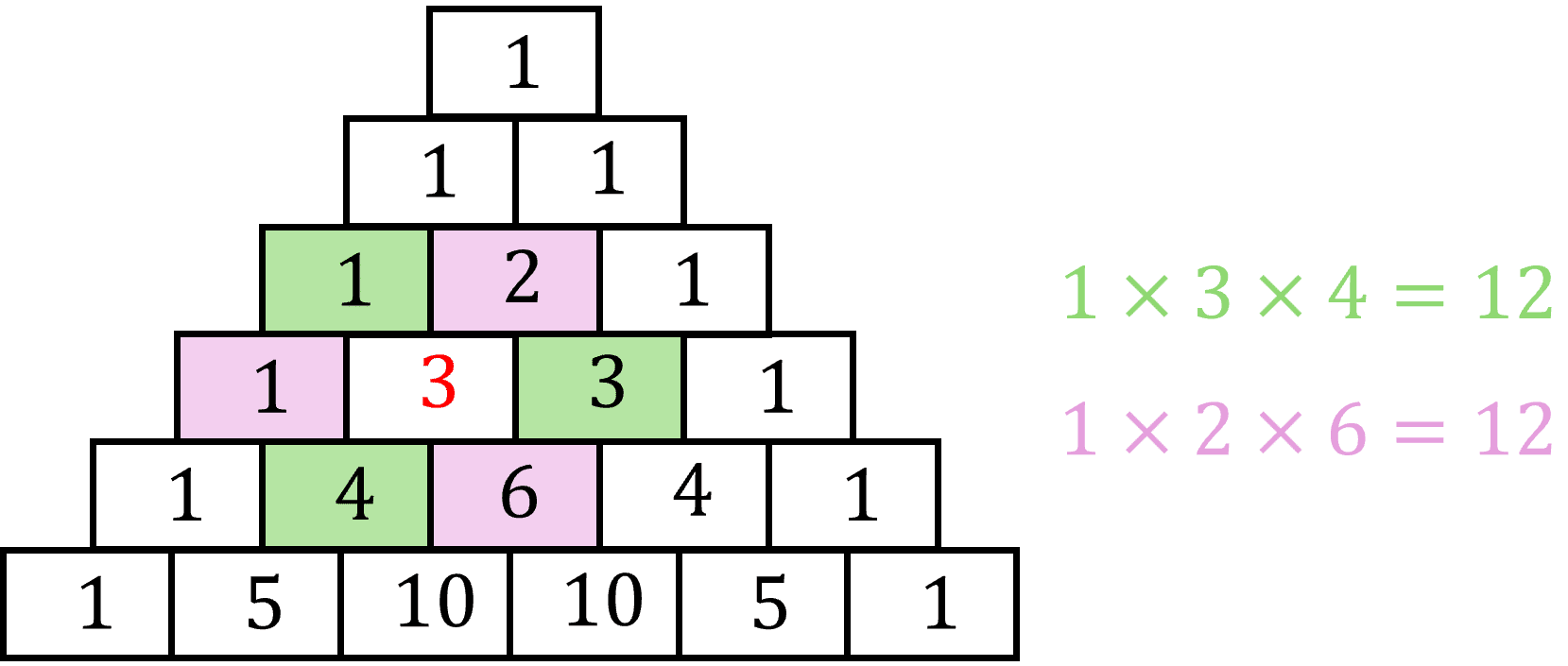
On remarque ainsi que si on considère un coefficient en particulier et qu’on multiplie, en alternant, les coefficients qui l’entourent (et ce, deux fois donc), les deux produits sont égaux.
Mathématiquement, cette propriété est donnée par la relation suivante : \(\begin{align} {{n-1}\choose{r-1}}{{n}\choose{r+1}}{{n+1}\choose{r}} = {{n-1}\choose{r}}{{n}\choose{r-1}}{{n+1}\choose{r+1}}\end{align}\)
Démonstration
Il suffit d’écrire les coefficients binomiaux sous leur forme développée et l’égalité devient évidente.
À lire également : 10 astuces sur les sommes – Niveau avancé
Liens entre le triangle de Pascal et des notions usuelles
Triangle de Pascal et Fibonacci
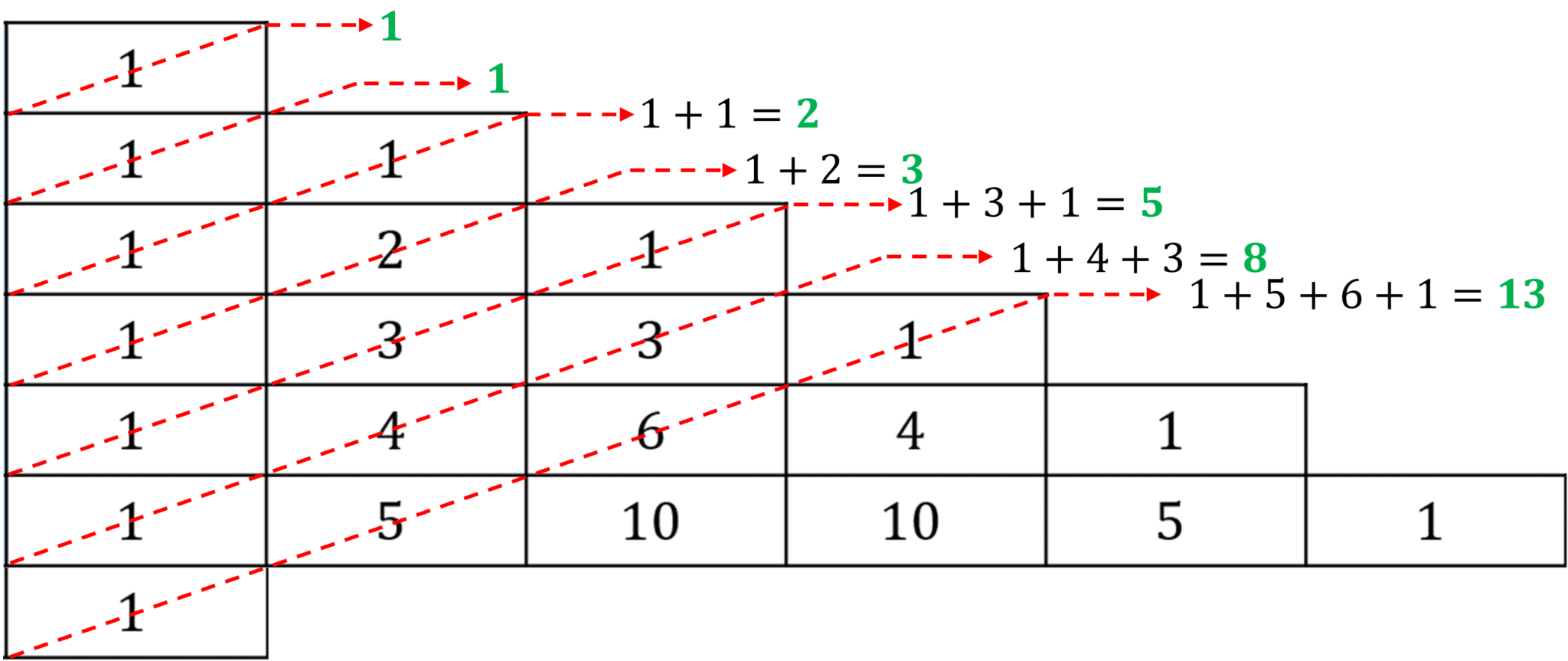
Que serait un article de mathématiques sans une référence au grand Fibonacci ? Heureusement, le triangle de Pascal nous sauve la mise, car on retrouve dans ce dernier la suite de Fibonacci ! En effet, si on considère les diagonales du triangle, lorsqu’on l’écrit sous la forme d’un escalier, on remarque qu’en additionnant les coefficients diagonaux, on obtient à chaque fois un nombre de la suite de Fibonacci, et dans l’ordre en plus !
Triangle et binôme de Newton
Comme tu l’as déjà remarqué, on a utilisé à plusieurs reprises le binôme de Newton pour démontrer des propriétés du triangle de Pascal. Cela s’explique par le fait que le triangle de Pascal et le binôme de Newton sont intrinsèquement liés.
On le constate notamment lorsqu’on veut développer un polynôme de la forme \((x+y)^n\).
Par exemple, pour \(n = 2\), on a \((x+y)^2 = \color{red}{1}.x^2 + \color{red}{2}xy + \color{red}{1}.y^2\)
Pour \(n = 3\), on a \((x+y)^3 = \color{red}{1}.x^3 + \color{red}{3}x^2y+\color{red}{3}xy^2 + \color{red}{1}.y^3\)
Ainsi, on observe que lorsqu’on développe \((x+y)^n\), on retrouve la \(n^{ième}\) ligne du triangle. Ce qui se traduit mathématiquement par la formule suivante : \(\forall n \in
\mathbb{N}, (x+y)^n = \sum_{p=0}^n{{n}\choose{p}}x^py^{n-p}\), c’est-à-dire la formule du binôme de Newton.
Triangle inversé et π
Pour cette propriété, il me faut considérer la diagonale ascendante, coloriée en beige : \(\text{Diag}=1\text{ }3\text{ }6\text{ }10\text{ }…\), puis l’inverser, ce qui donne :\[\begin{align}1\text{ }\text{ }\text{ }\text{ }\frac{1}{3}\text{ }\text{ }\text{}\text{ }\frac{1}{6}\text{ }\text{ }\text{ }\text{ }\frac{1}{10}\text{ }\text{ }\text{} \text{ }…\end{align}\]
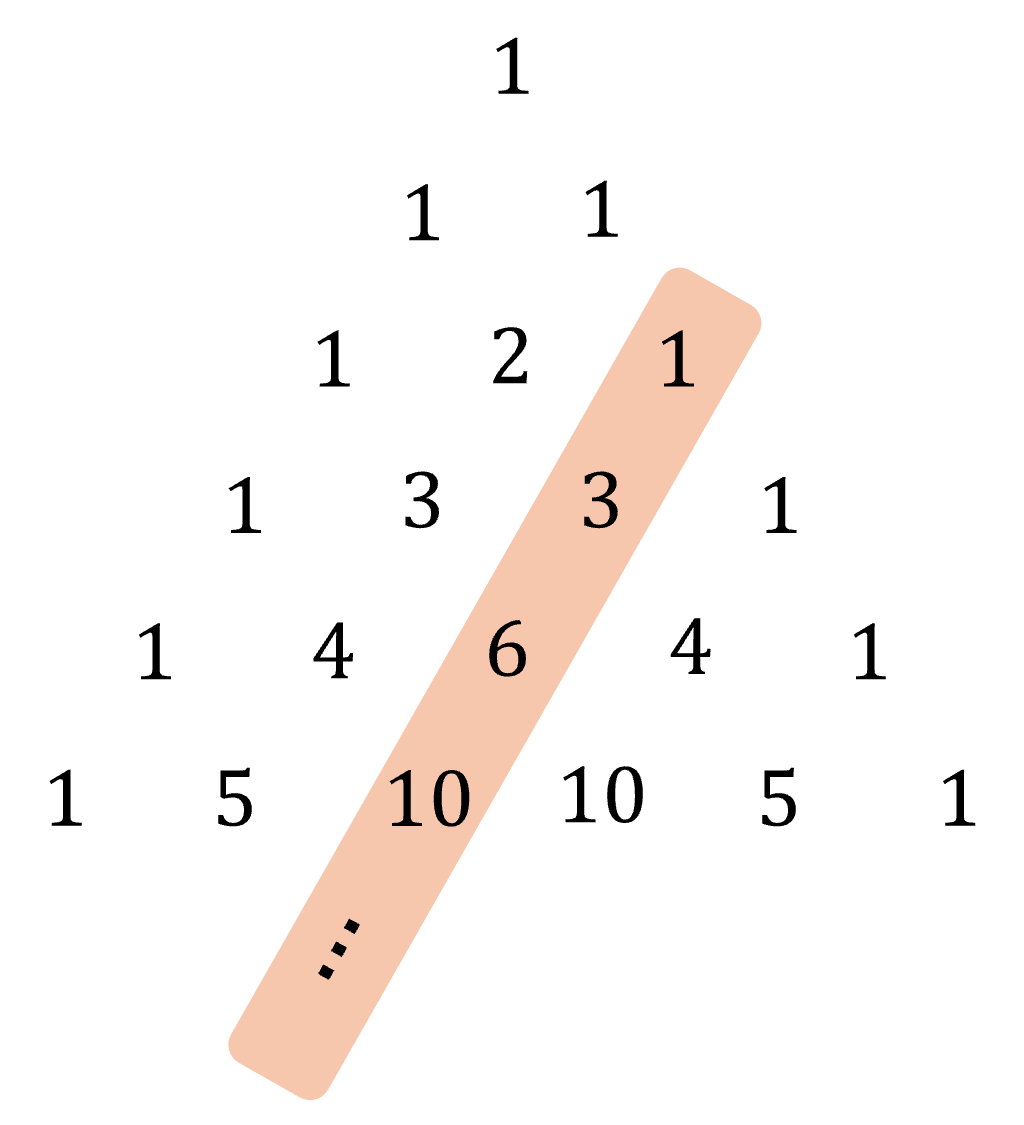
On fait désormais la somme alternée de ses coefficients (mais tous les deux signes !), ce qui permet d’exhiber la connexion entre le triangle de Pascal et \(\pi\) :
\[\begin{align}1\color{red}{+}\frac{1}{3}\color{red}{-}\frac{1}{6}\color{red}{-}\frac{1}{10}\color{red}{+}…\end{align} = \pi -2\]
Démonstration
Pour rappel, pour tout élément \(x\in]-1,1[,\arctan(x)=\sum_{n=0}^{+\infty}(-1)^n\frac{x^{2n+1}}{2n+1}\).
Ainsi en prenant \(x=1\) (ce qui est licite, compte tenu que\(\underset{n \ge 0}{\sum}\frac{(-1)^n}{2n+1}\) converge, en vertu du théorème spécial des séries alternées), on a :\[\frac{\pi}{4}=\sum_{n=0}^{+\infty}\frac{(-1)^n}{2n+1}\]
Donc :
\(\begin{align} \pi = 4\sum_{n=0}^{+\infty}\frac{(-1)^n}{2n+1}=4 \left (1-\frac{1}{3}+\frac{1}{5}-…\right ) &= 4-\frac{4}{3}+\frac{4}{5}-…\\&=2+2-\frac{4}{3}+\frac{4}{5}-… \\&=2+2\left (1-\frac{2}{3}+\frac{2}{5}-… \right ) \\&= 2+2\left ( 1-\color{green}{\frac{1}{2}-\frac{1}{2}}-\frac{1}{3}-\frac{1}{3}+\color{green}{\frac{1}{4}-\frac{1}{4}}+\frac{1}{5}+\frac{1}{5}-… \right )\text{(en vert, les termes ajoutés)}\\&=2+2\left [\left ( 1-\frac{1}{2}\right ) \color{red}{+} \left (\frac{1}{2}-\frac{1}{3}\right ) \color{red}{-}\left ( \frac{1}{3}-\frac{1}{4} \right )\color{red}{-}\left (\frac{1}{4}-\frac{1}{5}\right )\color{red}{+}…\right ] \end{align}\)
De plus, il vient par décomposition en éléments simples : \(\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}\), ce qui permet d’écrire :
\(\begin{align} \pi – 2 = 2\left [ \frac{1}{1\times 2}\color{red}{+}\frac{1}{2\times 3}\color{red}{-}\frac{1}{3\times 4} \color{red}{-}\frac{1}{4\times 5}\color{red}{+}…\right ]= 1 \color{red}{+}\frac{1}{3} \color{red}{-}\frac{1}{6}\color{red}{-}\frac{1}{10}\color{red}{+}… \end{align}\)
Ce qui clôt la démonstration : \[\fbox{\(\begin{align}1\color{red}{+}\frac{1}{3}\color{red}{-}\frac{1}{6}\color{red}{-}\frac{1}{10}\color{red}{+}…\end{align} = \pi -2\)}\]
Cette connexion entre le triangle de Pascal et le célèbre nombre \(\pi\) a été découverte par le mathématicien Jonas Castillo Toloza, en 2007.
Formule du produit et e
Nous avons vu précédemment qu’en faisant la somme des coefficients de chaque ligne, il apparaissait \(2^n\). Qu’en est-il si l’on fait le produit des coefficients de chaque ligne ? Pour cela notons ces produits \(p_n\), où \(n\) est le numéro de la \(n^{ième}\) ligne.
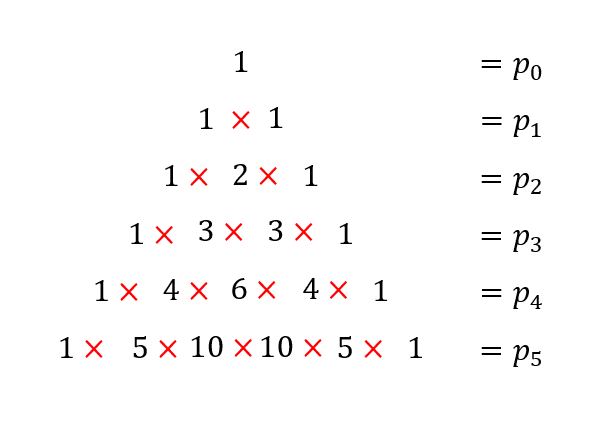
Ainsi, en multipliant le produit de la \( (n+1)^{ième}\) avec le produit de la \( (n-1)^{ième}\), et en divisant le tout par le produit de la \(n^{ième}\) ligne au carré, on obtient la quantité suivante : \(\frac{p_{n+1}\times p_{n-1}}{p_n^2}\), qui est égale à \(\left(1+\frac{1}{n}\right)^n\).
Dès lors, par passage à la limite, on obtient : \[\underset{n\rightarrow +\infty}{\lim}\frac{p_{n+1}\times p_{n-1}}{p_n^2}=\underset{n\rightarrow +\infty}{\lim}\left(1+\frac{1}{n}\right)^n=e\]
Démonstration
Soit \(n\in\mathbb{N}\).
Avant toute chose, réécrivons \(p_n\) sous une autre forme. Pour rappel, \(p_n\) correspond au produit des coefficients de la \(n^{ème}\) ligne, soit : \(\begin{align}p_n = \prod_{p=0}^{n}{{n}\choose{p}}&=\prod_{p=0}^n \frac{n!}{p!(n-p)!}\\&=(n!)^{n+1}\prod_{p=0}^n \frac{1}{p!(n-p)!}\text{ (il y a }n+1\text{ termes dans le produit)}\\&=(n!)^{n+1}\prod_{p=0}^n\left[\frac{1}{0!\color{red}{(n-0)!}}\times\frac{1}{1!\color{green}{(n-1)!}}\times…\times\frac{1}{\color{green}{(n-1)!}1!}\times\frac{1}{\color{red}{(n-0)!}0!}\right] \\&= (n!)^{n+1}\prod_{p=0}^n\left[\frac{1}{n!^2\times (n-1)!^2\times…\times 2!^2\times 1}\right]\\&= \frac{(n!)^{n+1}}{\prod_{p=0}^n (p!)^2}\end{align}\)
\(\begin{align}\text{Ainsi : }\frac{p_{n+1}\times p_{n-1}}{p_n^2}&=\frac{\frac{((n+1)!)^{n+2}}{\prod_{p=0}^{n+1} (p!)^2} \times \frac{((n-1)!)^n}{\prod_{p=0}^{n-1} (p!)^2}}{\left(\frac{(n!)^{n+1}}{\prod_{p=0}^n (p!)^2}\right)^2}\\&= \frac{(n+1)!^{n+2}(n-1)!^n}{[n!^{n+1}]^2}\frac{\prod_{p=0}^n (p!)^4}{\prod_{p=0}^{n+1}(p!)^2\times \prod_{p=0}^{n-1}(p!)^2} \\& =\frac{[(n+1)n(n-1)!]^{n+2}(n-1)!^n}{[(n(n-1)!)^{n+1}]^2} \frac{\color{blue}{n!^4} \color{green}{\prod_{p=0}^{n-1}p!^4}}{(n+1)^2 \color{blue}{n!^2} \color{blue}{n!^2} \color{green}{\prod_{p=0}^{n-1}p!^2} \color{green}{\prod_{p=0}^{n-1}p!^2} }\\&= \frac{(n+1)^{n+\color{blue}{2}}n^{n+2}\color{green}{(n-1)!^{n+2}(n-1)!^n}}{\color{blue}{(n+1)^2} n^{2n+2}\color{green}{(n-1)!^{2n+2}}}\\&= \frac{(n+1)^n}{n^n} \\&=\left (1+\frac{1}{n} \right )^n\end{align}\)
Ce qui donne, au voisinage de \(+\infty\) :
\(\left (1+\frac{1}{n}\right )^n = \exp(n\ln(1+\frac{1}{n}))=\exp(n[\frac{1}{n}+\underset{+\infty}{\mathcal{o}}(\frac{1}{n})]) = \exp(1+\mathcal{o}(1)) \underset{n \rightarrow + \infty}{\sim} e \underset{n\rightarrow + \infty}{\rightarrow} e \)
Ce qui prouve enfin que : \[\fbox{\(\underset{n\rightarrow +\infty}{\lim}\frac{p_{n+1}\times p_{n-1}}{p_n^2}=\underset{n\rightarrow +\infty}{\lim}\left(1+\frac{1}{n}\right)^n=e\)}\]
Triangle de Sierpiński
Cette fois-ci, on va modifier le triangle en appliquant une règle simple : on remplace tous les coefficients impairs par 1 et tous les coefficients pairs par 0. Par conséquent, on obtient un triangle codé en binaire.
Maintenant, si on met en évidence les coefficients pairs et impairs, on obtient :
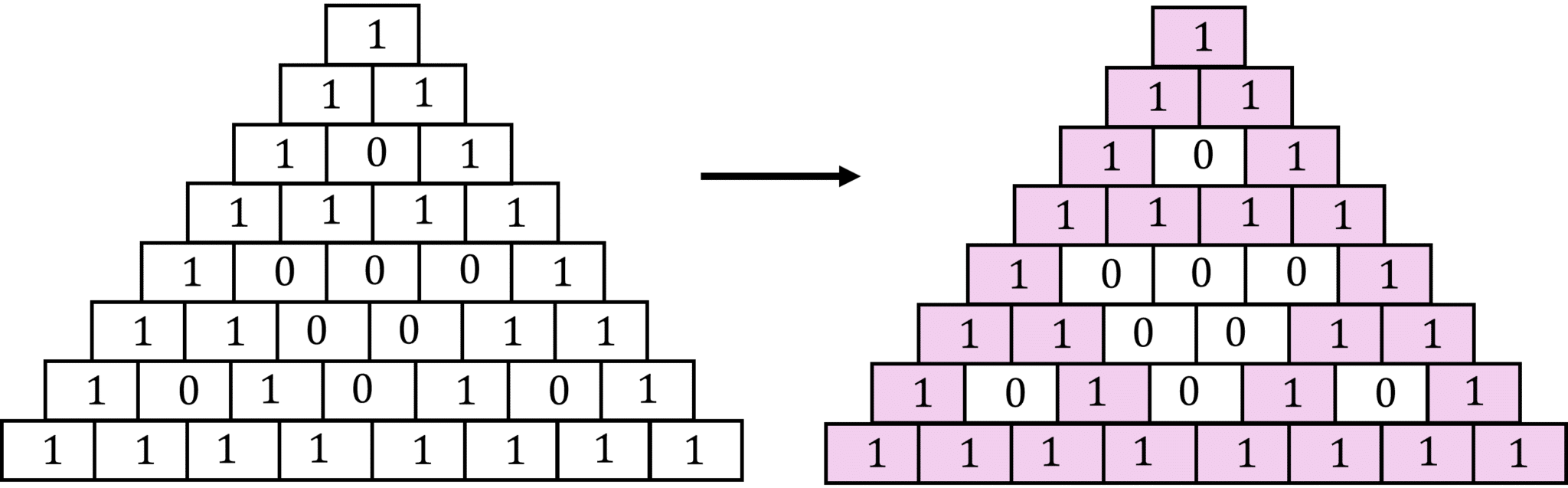
Peut-être as-tu remarqué le triangle des Illuminati, ou bien celui de la Triforce, mais mathématiquement, ce triangle porte un nom très particulier : on l’appelle le triangle de Sierpiński. Le triangle présenté est un peu trop petit, mais si on prend un triangle avec plus de coefficients, on remarque qu’il y a des patterns.
Triangle et nombres premiers
On conserve notre triangle avec des coefficients binaires et cette fois-ci, on convertit chaque ligne du binaire vers les nombres en base 10 (les nombres normaux tout simplement), ce qui donne :
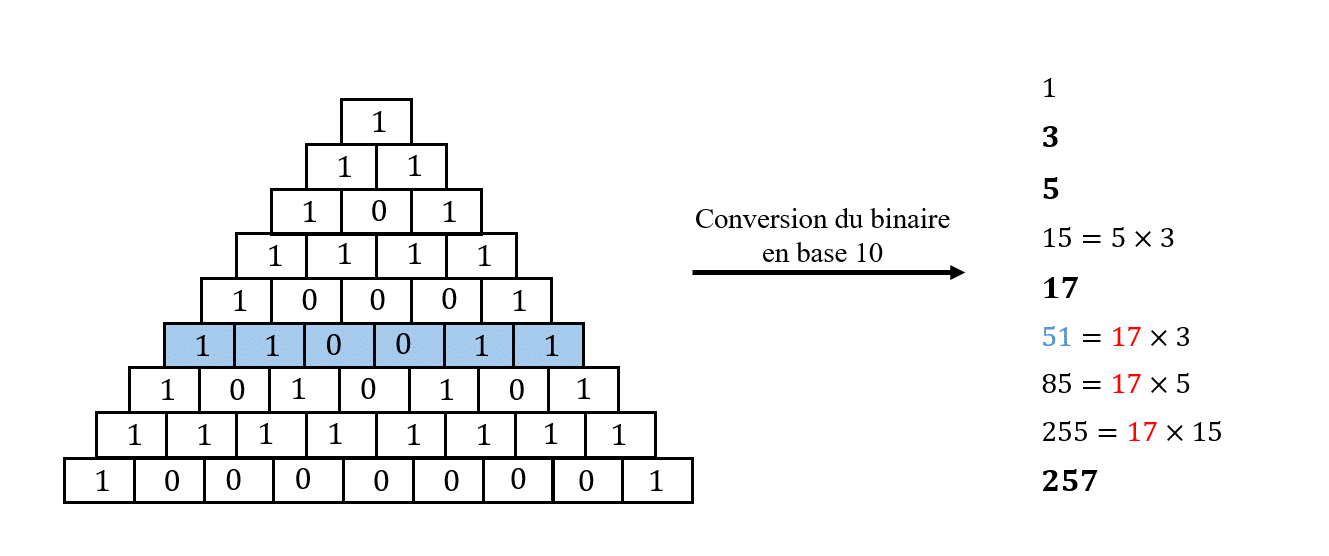
Ainsi, on remarque que le triangle nous donne un nombre premier (\(5\) par exemple), puis le multiplie avec les nombres (pas forcément premiers) trouvés précédemment (\(5 \times 3)\) et une fois qu’il a fini ce processus, il nous redonne un nouveau nombre premier.
Le triangle de Pascal sur Python
Voilà un script qui te permettra de construire le triangle de Pascal :
La ligne \(2\) crée la structure du triangle de Pascal, en créant une liste de listes composées de zéros et dont la longueur de chaque élément (qui sont eux-mêmes des listes) varie selon la valeur de \(n\), le nombre de lignes que l’on souhaite voir dans le triangle de Pascal.
La ligne \(3\) initialise la première ligne du triangle de Pascal.
Les lignes \(4\), \(5\) et \(6\), quant à elles, initialisent la valeur des extrémités du triangle.
Les lignes \(7\) et \(8\) construisent le triangle de Pascal, à l’aide de la relation de Pascal, vue précédemment.
Notons que la fonction \(\color{blue}{\text{pascal}}\) est codée de façon itérative (présence de boucles), mais qu’elle pourrait également être écrite de façon récursive.
Enfin, on peut afficher le triangle de Pascal, à l’aide de la fonction suivante :
Ainsi, pour \(n=6\), la fonction renvoie :

À ce jour, il n’existe pas d’annales ayant mis en exergue le triangle de Pascal (à notre connaissance), mais on pourrait très bien imaginer un concepteur souhaitant faire une partie du sujet avec des questions Python portant sur le triangle de Pascal…
À lire ensuite : La méthode de Monte-Carlo d’estimation sur Python
Conclusion
Ainsi, tu as pu découvrir les nombreux secrets que cache le triangle de Pascal. Toutefois, la liste des propriétés présentées est bien loin d’être exhaustive. Certaines propriétés ont été mises de côté (trop techniques ou bien trop tirées par les cheveux, voire les deux…) et d’autres restent encore à découvrir !
Si tu souhaites maintenant t’exercer en mathématiques (et espérer peut-être démontrer une nouvelle propriété du triangle…), tu peux retrouver ici le méga-répertoire qui contient toutes les annales de concours et les corrigés ! Tu peux également accéder ici à toutes nos autres ressources mathématiques.