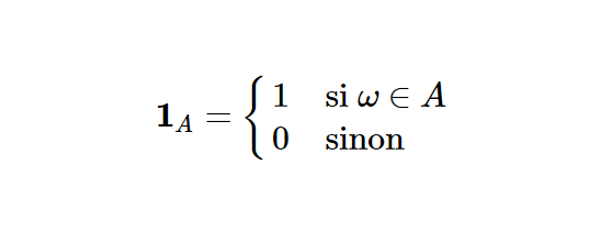La variable indicatrice n’est pas directement au programme, mais tu peux faire la différence le jour du concours si tu maîtrises son utilisation, puisqu’elle est tombée plusieurs fois dans des sujets d’écrits. Voici ce qu’il faut savoir.
Définition
La variable indicatrice, notée \(\mathbb{1}\), est une variable aléatoire prenant comme valeur 0 ou 1.
On la définit mathématiquement ainsi : \[\mathbf{1}_{A} =
\begin{cases} 1 &\text{si} \; \omega \in
A \\ 0 &\text{sinon}\end{cases}\]
Pour approfondir la notion, tu peux également aller voir la nuance avec une fonction indicatrice.
Pourquoi faut-il savoir utiliser la variable indicatrice ?
Les concepteurs l’utilisent
Bien que la variable indicatrice ne soit pas officiellement au programme, les concepteurs utilisent régulièrement cette notation. Il te faut donc être familiarisé(e) avec cette notation pour ne pas perdre de temps le jour du concours.
Tu pourras d’ailleurs remarquer que, sur ce PDF du Maths II 2002, le candidat a mis des points d’interrogation lorsque le sujet a introduit l’indicatrice de l’évènement \(A_n\). Savoir ce qu’est une indicatrice te fera donc gagner des points.
Voici comment résoudre la question 3a) de la partie III de ce Maths II de 2002.
Énoncé
On note \( M \) un majorant de \( |f| \) sur \([0,+\infty[\).
Soit \(\epsilon\) un réel strictement positif. Pour tout entier naturel \( n \), on note \( A_n \) l’évènement :
\[ A_n = \left\{ \left| f\left(\frac{S_n}{n}\right) – f(x) \right| \leq \epsilon \right\} \]
et \(\mathbb{1}_{A_n}\) son indicatrice. Justifier l’inégalité suivante :
\[
|f\left(\frac{S_n}{n}\right) – f(x)| \leq \epsilon \mathbb{1}_{A_n} + 2M( 1 – \mathbb{1}_{A_n})
\]
Corrigé
Lorsque tu rencontres la variable indicatrice dans un sujet, il faut généralement que tu penses à faire une disjonction de cas. C’est ce que l’on va faire :
Si \(\omega \in A_n\)
Alors
\[
| f\left(\frac{S_n}{n}\right) – f(x) | \leq \epsilon
\]
et
\[\begin{align}\epsilon \mathbb{1}_{A_n} + 2M( 1 – \mathbb{1}_{A_n}) &=
\epsilon \cdot 1 + 2M \cdot (1 – 1)\quad \text{car} A_n \text{est réalisé}\\ &= \epsilon \end{align}
\]
Donc :
\[
\fbox{Si \( \omega \in A_n \)\(|f\left(\frac{S_n}{n}\right) – f(x)| \leq \epsilon \mathbb{1}_{A_n} + 2M(1 – \mathbb{1}_{A_n})\)}.
\]
Si \( \omega \notin A_n\)
On a \[\begin{align} |f\left(\frac{S_n}{n}\right) – f(x)| &\leq |f\left(\frac{S_n}{n}\right)| + |f(x)| \\&\leq M + M \quad \text{car M est un majorant de |f|}\\&= \epsilon \cdot 0 + 2M \cdot (1 – 0) \\&= \epsilon \mathbb{1}_{A_n} + 2M( 1 – \mathbb{1}_{A_n})\quad \text{car} A_n \text{n’est pas réalisé}\end{align}\]
Donc :
\[
\fbox{Si \( \omega \notin A_n \)\(|f\left(\frac{S_n}{n}\right) – f(x)| \leq \epsilon \mathbb{1}_{A_n} + 2M(1 – \mathbb{1}_{A_n})\)}.
\]
Et donc, finalement, l’inégalité suivante est toujours vraie
\[\fbox{\(
|f\left(\frac{S_n}{n}\right) – f(x)| \leq \epsilon \mathbb{1}_{A_n} + 2M( 1 – \mathbb{1}_{A_n})\)}
\]
Tu peux résoudre de nouveaux problèmes
Tu auras peut-être remarqué que les variables indicatrices suivent des lois de Bernoulli. En reprenant la variable indicatrice du début, on a \(\mathbb{1}_A \hookrightarrow \mathcal{B}(\mathbb{P}(A))\).
Savoir cela permet de gagner du temps lors de résolutions de problèmes, car on pourra utiliser toutes les propriétés autour de la loi de Bernoulli. On aura notamment \( \mathbb{E}(\mathbb{1}_A) = \mathbb{P}(A) \)
Par exemple, pour la démonstration de l’inégalité de Markov, il est possible de faire une disjonction de cas dans le cas discret. Tu peux la voir sur cet article qui a déjà été écrit. Mais la fonction indicatrice permet de gagner énormément de temps et de travailler dans le cas général.
Voici la démonstration en l’utilisant.
Proposition
Soit \(X\) une variable aléatoire positive admettant une espérance. On a : \[
\forall a \in \mathbb{R}_{+}^{*}, \quad \mathbb{P}(X \geq a) \leq \frac{\mathbb{E}(X)}{a}
\]
Démonstration
Soit \( a \in \mathbb{R}_{+}^{*}\)
Puisque X est positive, il est toujours vrai que : \[a\mathbb{1}_{X\geq a} \leq X\]
Par positivité de l’espérance, on en déduit que : \[a\mathbb{E}(\mathbb{1}_{X\geq a}) \leq \mathbb{E}(X)\]
Donc : \[aP(X \geq a) \leq \mathbb{E}(X)\]
Et puisque \(a \ne 0\) :
\[\fbox{\(P(X \geq a) \leq \frac{\mathbb{E}(X)}{a}\)}\]
Tu peux définir différemment des évènements
Énoncé
Soit \(X\) une variable aléatoire et \( (X_n)_{n \geq 1} \) une suite de variables aléatoires. On suppose que \(X\) et les \(X_n\) admettent une espérance et qu’il existe un réel \(K > 0\) tel que \(|X| \leq K\) et \(\forall n \in \mathbb{N}^*\), \(|X_n| \leq K\).
On suppose que la suite \( (X_n)_{n \geq 1} \) converge en probabilité vers \(X\). Montrer que \(\lim_{n \to +\infty} \mathbb{E}(|X_n – X|) = 0\).
Corrigé
Soit \(\epsilon > 0\) et le système complet d’évènements \(\{|X_n – X| > \epsilon, |X_n – X| \leq \epsilon\}\). Grâce à la fonction indicatrice, on peut écrire l’inégalité suivante :
\[
|X_n – X| = |X_n – X| \times \mathbf{1}_{\{|X_n – X| > \epsilon\}} + |X_n – X| \times \mathbf{1}_{\{|X_n – X| \leq \epsilon\}}.
\]
En s’intéressant à l’espérance, on a :
\[
\mathbb{E}(|X_n – X|) = \mathbb{E}(|X_n – X| \times \mathbf{1}_{\{|X_n – X| > \epsilon\}}) + \mathbb{E}(|X_n – X| \times \mathbf{1}_{\{|X_n – X| \leq \epsilon\}}),
\]
donc :
\[
\mathbb{E}(|X_n – X|) \leq 2K \times \mathbb{E}(\mathbf{1}_{\{|X_n – X| > \epsilon\}}) > \epsilon) + \epsilon \times \mathbb{E}(\mathbf{1}_{\{|X_n – X| \leq \epsilon\}}),
\]
d’où : \[
\mathbb{E}(|X_n – X|) \leq 2K \cdot P(|X_n – X| > \epsilon) + \epsilon \cdot P(|X_n – X| \leq \epsilon),
\]
alors :
\[
\mathbb{E}(|X_n – X|) \leq 2K \cdot P(|X_n – X| > \epsilon) + \epsilon.
\]
Et puisque \(\lim \limits_{n \to +\infty}P(|X_n – X| > \epsilon) = 0\) car \(X_n \overset{\mathbb{P}}
{\rightarrow} X\) :
\[
\exists n_0 \in \mathbb{N}^{*}, \forall n \geq n_0, \ 2K \cdot P(|X_n – X| > \epsilon) \leq \epsilon.
\]
Ainsi, pour \(n \geq n_0\), on a
\[
\mathbb{E}(|X_n – X|) \leq 2 \epsilon,
\]
et comme \(\epsilon > 0\) est quelconque, on a bien
\[
\lim_{n \to +\infty} \mathbb{E}(|X_n – X|) = 0.
\]
Objets ressemblants
La variable indicatrice s’utilise principalement en probabilité. Mais il existe des objets qui ressemblent à la variable indicatrice, et tu dois être familiarisé(e) avec.
La fonction indicatrice
Il est possible que tu croises la fonction indicatrice qui associe une variable (x et t, la plupart du temps) et un ensemble I.
Par exemple :\[\mathbf{1}_{I}^{(t)} =
\begin{cases} 1 &\text{si} \; t \in
I \\ 0 &\text{sinon}\end{cases}\]
On peut donc définir cette fonction f de deux manières :
\[ f(x) =
\begin{cases} 3e^{-3x}
&\text{si} \; x \in
[0,+\infty[ \\ 0 &\text{sinon}
\end{cases}\]
Mais aussi :
\[ f(x) =3e^{-3x}\mathbb{1}_{[0,+\infty[}^{(x)}\]
Tu rencontreras souvent cette notation dans les exemples de probabilités à densité, mais pas que…
Le symbole de Kronecker
Tu le croiseras dans le domaine des matrices. Il est défini ainsi :
\[
\delta_{ij} =
\begin{cases}
1 & \text{si } i = j \\
0 & \text{si } i \neq j
\end{cases}
\]
Voici un article qui t’éclairera sur le symbole de Kronecker.
Sujets avec la variable indicatrice
Voici quelques sujets qui évoquent la variable indicatrice :
N’hésite pas à consulter toutes nos ressources mathématiques !