Les notions hors programme se destinent principalement aux candidats visant les trois Parisiennes. Cet article te propose de découvrir les variables aléatoires symétriques. Tu retrouveras les propriétés les plus intéressantes autour de cette notion afin d’y être pleinement sensibilisé(e) et de ne pas être pris(e) au dépourvu le jour des concours.
Les variables aléatoires symétriques, c’est quoi ?
Une variable aléatoire \( X \) est dite symétrique lorsque la loi de \( -X \) est identique à celle de \( X \).
En d’autres termes, pour tout \( x \) dans l’ensemble des valeurs possibles de \( X (Ω) \), on a :
\[P(X=x)=P(X=−x)\]
Cas discret
Dans le cas discret, une variable aléatoire \( X \) est dite symétrique si pour tout \( x \) dans son ensemble de valeurs possibles, la probabilité \( P(X=x) \) est égale à la probabilité \( P(X=-x) \).
En d’autres termes, la distribution de probabilité est identique de part et d’autre d’un certain point.
Cas continu
Pour une variable aléatoire continue, la symétrie est définie de manière similaire, mais avec des densités de probabilité.
Une variable aléatoire continue \( X \) est dite symétrique si sa densité de probabilité \( f(x) \) satisfait la condition \( f(x) = f(-x) \) pour tout \( x \) dans son domaine.
Propriétés
Symétrie centrale
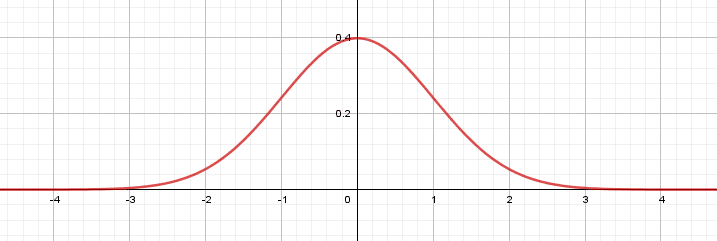
Graphiquement, les variables aléatoires symétriques présentent une symétrie centrale dans leur distribution.
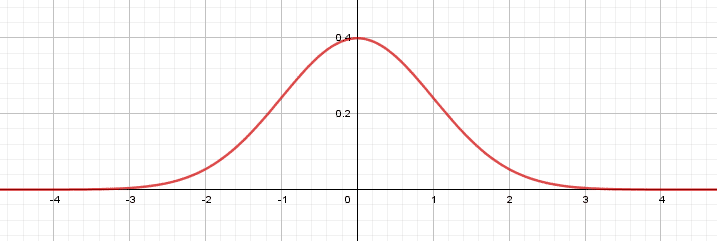
Espérance nulle
Si une variable aléatoire est symétrique et admet une espérance, alors son espérance est nulle.
Preuve dans le cas discret
Soit \( X \) une variable aléatoire discrète définie sur \( Ω = N \cap P \) où \( P = \{n \in \mathbb{N}^{+}, n \in Ω \} \text{ et } N= \{-n, n \in P \} \), admettant une espérance. Si \( Ω \) est finie, alors :
\[ E(X) = \sum_{k \in Ω}kP(X=k) = \sum_{k \in N}kP(X=k) + \sum_{k \in P}kP(X=k) = \sum_{k \in P}-kP(X=k) + \sum_{k \in P}kP(X=k) = 0. \]
Si \( Ω \) n’est pas finie, on prouve de même que \( E(X) = 0 \) en manipulant dans un premier temps la somme partielle de \( sum_{k \in Ω}kP(X=k) \), puis en utilisant la linéarité de la sommation comme dans la démonstration, et, enfin, en passant à la limite aux bornes.
Preuve dans le cas continu
Soit \( X \) une variable aléatoire discrète définie sur \( Ω = N \cap P \) où \( P = \{ x \in \mathbb{R}^{+}, x \in Ω \} \text{ et } N= \{ -x, x \in P \} \), admettant une espérance. Si \( Ω \) ne contient aucune singularité pour \( x \mapsto xf(x) \), alors :
\[ E(X) = \int_{x \in Ω}xf(x)\text{dx} = \int_{x \in N}xf(x)\text{dx} + \int_{x \in P}xf(x)\text{dx} = \int_{x \in P}-xf(x)\text{dx} + \int_{x \in P}xf(x)\text{dx} = 0. \]
Si \( Ω \) contient une ou plusieurs singularités pour \( x \mapsto xf(x) \), on prouve de même que \( E(X) = 0 \) en manipulant dans un premier temps \[\int xf(x)\text{dx}\] sur un intervalle réduit ne contenant aucune singularité, puis en utilisant la linéarité de l’intégration comme dans la démonstration, et, enfin, en passant à la limite aux bornes.
Moments d’ordre impair nuls
Les moments d’ordre impair d’une variable aléatoire symétrique sont également nuls.
Si \( X \) est une variable aléatoire discrète, symétrique, et admettant un moment d’ordre impair \( k \in \mathbb{N} \), la démonstration est alors la même que précédemment.
Transformation par une fonction impaire
Généralement, si \( X \) est une variable aléatoire symétrique et \( g \) est une fonction impaire et bijective, alors \( Y=g(X) \) est symétrique.
Exemple
Soit \( X \) une variable aléatoire discrète définie sur \( Ω \), symétrique, et \( g \) une fonction impaire et bijective sur \( g(Ω) \). On rappelle, et on peut montrer simplement que, comme \( g \) est impaire, \( g^{-1} \) est aussi impaire.
Soit \( x \in g(Ω) \), \( P(Y=k)=P(g(X)=x)=P(X=g^{-1}(x))=P(X=-g^{-1}(x))=P(X=g^{1}(-x))=P(g(X)=-x)=P(Y=-x) \).
Remarque
Une variable aléatoire suivant une loi normale centrée est symétrique.
N’hésite pas à consulter toutes nos ressources mathématiques.