Il est très courant, dans les sujets de mathématiques, que l’on te demande d’écrire un script Python dont l’objectif est le tri d’une liste. C’est pourquoi je vais t’introduire les quatre principaux algorithmes de tri avancés sur Python, en t’expliquant leur principe et en les comparant les uns aux autres, afin de mieux appréhender leurs intérêts.
Introduction
Avant de commencer sur l’aspect formel du sujet, les algorithmes de tri gagnent de leurs sens pour la manipulation des bases de données, qui nécessitent des tableaux triés, donc a fortiori, des listes triées.
Avant toute chose, par souci de pédagogie, je considère la représentation des listes Python suivante :

De plus, on cherchera toujours à trier la liste de façon croissante. C’est-à-dire que l’élément le plus petit sera à l’extrémité gauche et l’élément le plus grand sera à l’extrémité droite de la liste.
Enfin, nous chercherons toujours à trier des entiers. Toutefois, les algorithmes de tri peuvent aussi être utilisés pour trier des mots par ordre alphabétique, par exemple.
Les principaux types d’algorithmes de tri
L’algorithme de tri par insertion
Commençons par l’algorithme de tri le plus intuitif : le tri par insertion. Cet algorithme est celui qui vient en premier à l’esprit. C’est notamment celui-ci qu’utilisent les joueurs de cartes pour trier leurs jeux.
Le principe de cet algorithme est le suivant : il considère chaque élément de la liste à trier et l’insère parmi les éléments déjà triés.
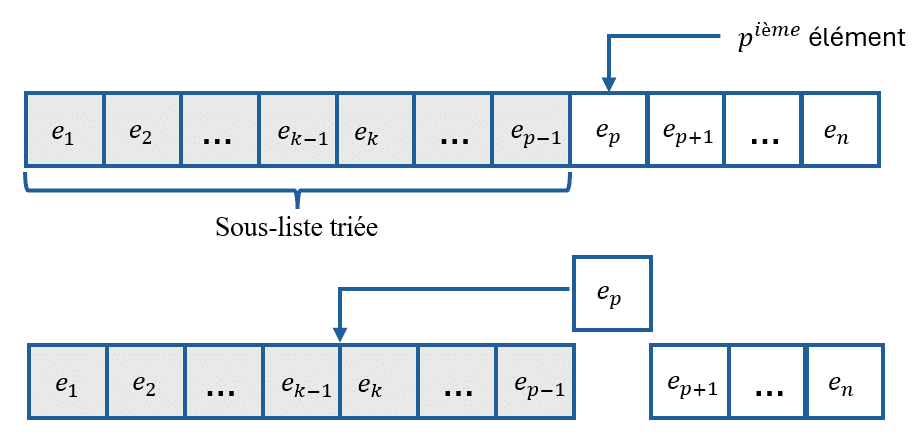
Pour aller plus loin, considérons la liste \([\color{blue}{e_1,…,e_{p-1}},e_p,…,e_n]\) dans laquelle les \(\color{blue}{p-1}\) premiers éléments sont triés et le \(p-ième\) élément de la liste que l’on souhaite insérer parmi les \(\color{blue}{p-1}\) premiers éléments déjà triés.
Dans cette situation, les éléments qui précèdent \(e_p\) sont triés et les éléments qui succèdent \(e_p\) ne sont pas triés. L’algorithme comparera alors le \(p-ième\) élément à chaque élément qui le précède et l’insérera, petit à petit, à la position adéquate.
Passons désormais à un exemple concret
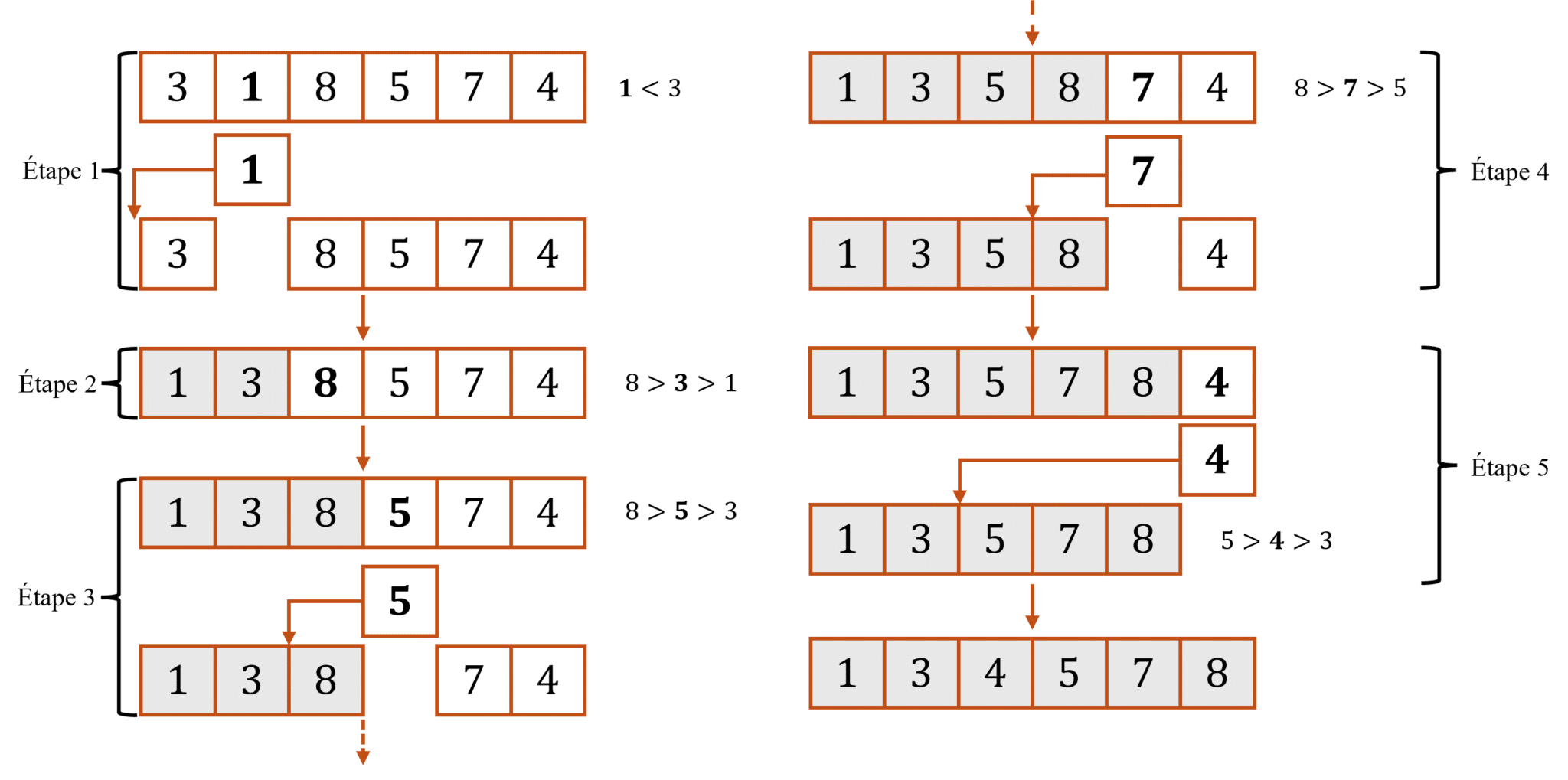
Considérons la liste \([3,1,8,5,7,4]\) que l’on souhaite trier à l’aide du tri par insertion. Nous obtenons le schéma ci-dessous, dans lequel la remontée de chaque élément étape par étape a été omise dans un premier temps, pour des soucis de lisibilité :
Étape 1 : La première clé est le deuxième élément de la liste. C’est-à-dire \(1\), que l’on compare avec le premier élément de la liste, soit \(3\), et comme \(1<3\), on échange leur place. On a donc la sous-liste triée : \([1,3]\).
Étape 2 : La deuxième clé est \(8\), que l’on compare avec \(3\). Étant donné que \(8>3\), rien ne se passe. Nous avons ainsi la sous-liste triée suivante : [1, 3, 8].
Étape 3 : La troisième clé est \(5\), que l’on compare avec \(8\). Étant donné que \(5<8\), on échange leur place. De plus, \(5>3\), donc rien ne se passe et nous obtenons ainsi : [1, 3, 5, 8].
Étape 4 : De façon analogue à l’étape 3. Ce qui permet d’avoir la sous-liste triée suivante : [1, 3, 5, 7, 8].
Étape 5 : La cinquième clé est \(4\), que l’on compare avec \(8\), comme \(4<8\), on échange leur place. On compare dès lors \(4\) avec \(7\), étant donné que \(4<7\), leur place sont échangées, et ainsi de suite. Comme le décrit le schéma ci-dessous, qui décrit l’insertion étape par étape de l’élément \(4\) parmi les éléments déjà triés :
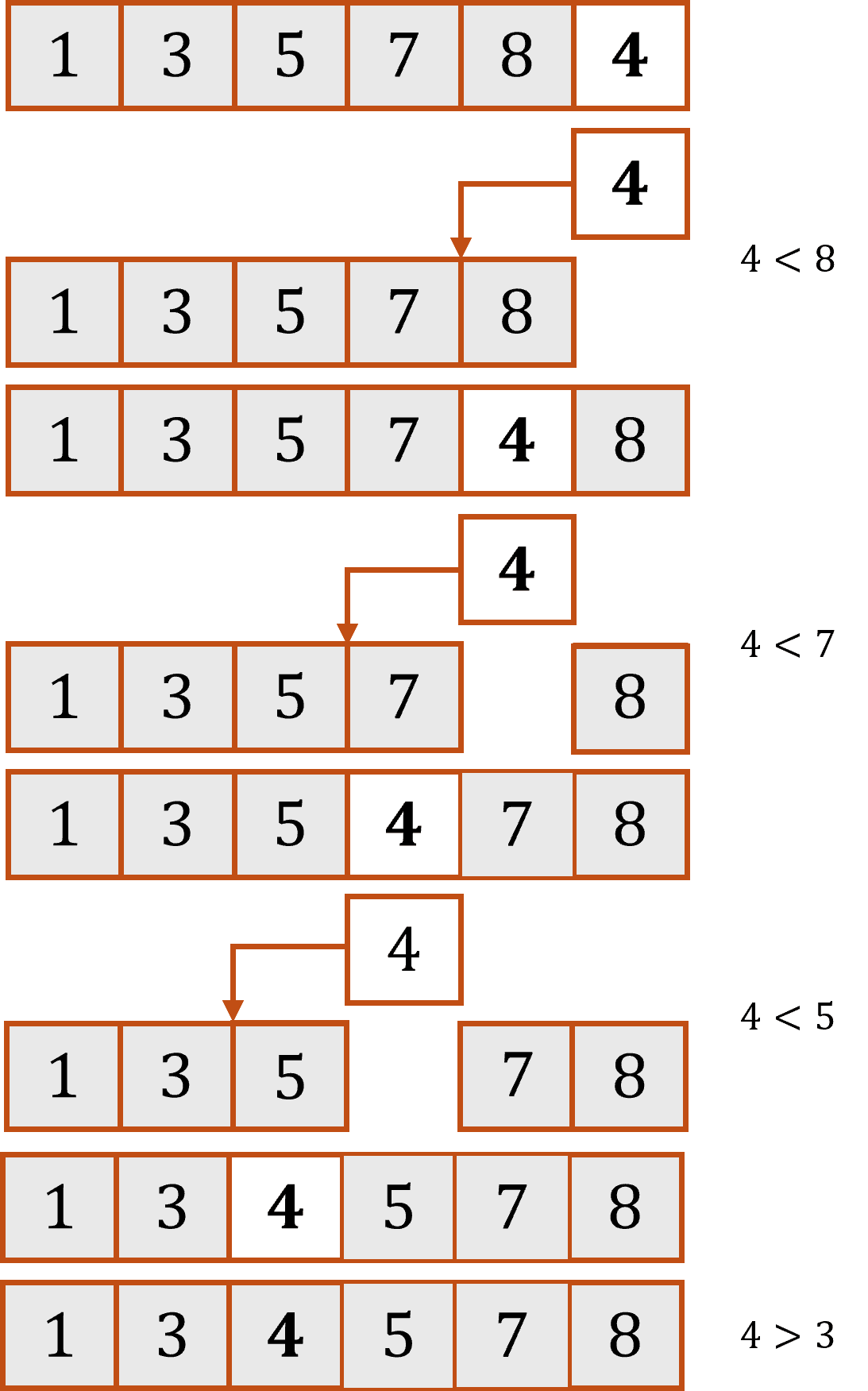
Le principe de l’algorithme de tri par insertion étant détaillé, passons désormais à son implémentation sur Python :
Les lignes \(2\) et \(3\) permettent de considérer chaque élément de la liste pour les ranger à la position adéquate.
La ligne \(4\) assure la terminaison de l’algorithme, condition nécessaire pour un algorithme de tri.
Les lignes \(5\), \(6\) et \(7\) effectuent la remontée de la clé, si elle n’est déjà par triée.
Je pense que tu l’auras compris, cet algorithme de tri porte bien son nom, puisque l’on insère un élément (que l’on souhaite trier) petit à petit dans une liste déjà triée, jusqu’à l’insérer à la position adéquate.
Ceci étant dit, passons désormais au second algorithme de tri, celui du tri par sélection.
Algorithme de tri par sélection
Le principe de l’algorithme de tri par sélection est de déterminer le plus petit élément de la liste à trier et de le placer au début de la liste (d’indice 0), pour ensuite réitérer le même processus, mais cette fois-ci en plaçant le plus petit élément à l’indice 1 de la liste, etc., jusqu’à ce que la liste soit triée.
Un exemple valant mieux que mille mots, trions la liste suivante \(L=[5, 9, 6, 3, 7]\) avec l’algorithme de tri par sélection :
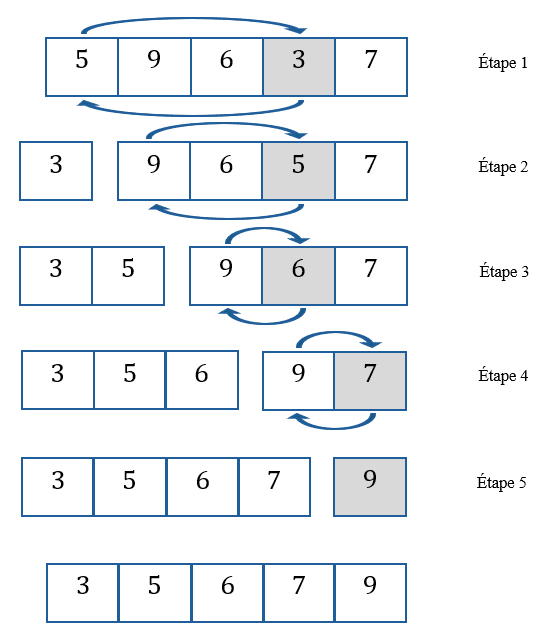
Étape 1 : Le plus petit élément de \(L\) est \(3\), que je place au début de la liste, soit à l’indice \(0\).
Étape 2 : Le plus petit élément de \(L[1 :]=[9,6,5,7]\) est \(5\), que je place au début de \(L[1 :]\), soit à l’indice \(1\) de \(L\).
Et on réitère le processus jusqu’à l’étape 5, dans laquelle on a \(L[4 :]= [9]\), qui est évidemment le plus petit élément de \(L[4 :]\), que l’on place au début de \(L[4 :]\) soit à la fin de \(L\).
Une fois que tu as compris le principe de cet algorithme, il t’est plus aisé de l’implémenter sur Python. Et comme tu l’as compris, avant d’écrire l’algorithme à proprement parlé de tri par sélection, il te faut construire une fonction qui puisse déterminer le plus petit élément d’une liste donnée :
La ligne \(4\) assure un majorant de n’importe quel élément de la liste.
Les lignes \(5\) à \(8\) permettent le parcours de la liste, élément par élément, afin de déterminer le plus petit.
Remarque
On peut également utiliser la fonction minimum de Python qui, pour une liste donnée \(L\), en paramètre de la fonction, renvoie le plus petit élément de la liste :
Dès lors que l’on peut déterminer le minimum d’une liste donnée, implémentons l’algorithme de tri par sélection sur Python :
La ligne \(3\) fixe à chaque itération, le premier élément de la liste \(L[i :]\).
Les lignes \(4\) et \(5\) déterminent le plus petit élément de la liste \(L[i :]\), ainsi que son indice dans \(L[i :]\).
Les lignes \(6\) et \(7\) échangent le plus petit élément de \(L[i :]\) avec le premier élément de \(L[i :]\).
Cet algorithme est appelé ainsi, étant donné que l’on sélectionne pour chaque liste \(L[i:]\) son plus petit élément que l’on place au début de la liste \(L\).
Cela étant dégrossi, passons à l’avant-dernier algorithme de tri, l’algorithme de tri fusion.
Algorithme de tri fusion
L’algorithme de tri fusion, crée par John von Neumann en 1945, utilise la méthode de « diviser pour régner » et repose sur deux principes :
- la division de la liste à trier, qui s’effectue naturellement de façon récursive ;
- la phase de remontée, dans laquelle deux listes triées sont fusionnées pour en former qu’une seule. Cette deuxième étape s’écrit aussi naturellement de façon récursive.
Continuons sur un exemple, on cherche à trier la liste \(L = [1, 9, 4, 6, 7, 2, 8, 5]\).
Comme on l’a dit précédemment, nous devons diviser la liste en sous-listes de taille égale (à \(1\) près, selon si la liste contient un nombre pair d’éléments ou non), comme tu peux le voir dans le schéma ci-dessous, qui se lit de bas en haut :
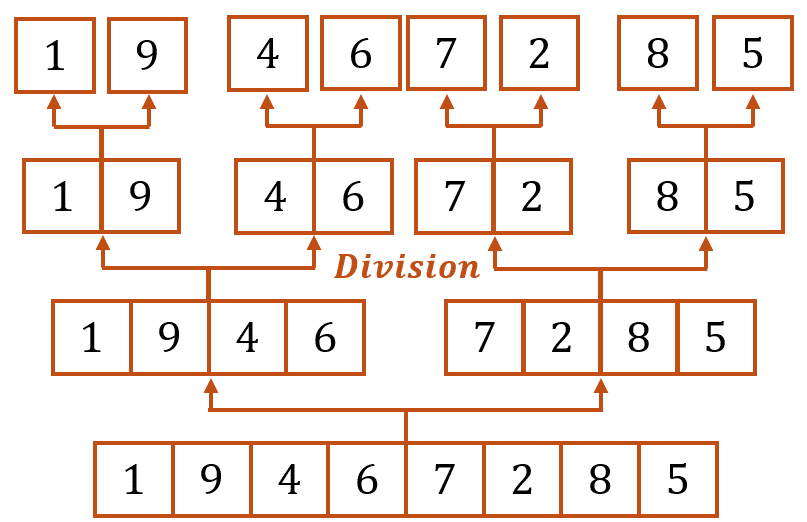
Ainsi, dans l’exemple considéré, la division de \(L\) donne \(8\) sous-listes triées, étant donné que chaque sous-liste est constituée d’un seul élément.
Cela étant fait, passons à la seconde phase : la fusion
Cette phase consiste à fusionner deux listes triées pour n’en former qu’une seule, qui soit triée.
Ainsi, considérons deux listes triées \(L_1\) et \(L_2\). La fusion compare le premier élément des deux listes. Supposons que ça soit le premier élément de \(L_1\) qui soit le plus grand, dans ce cas, on ajoute cet élément à une liste préalablement créée pour la fusion, et \(L_1\) voit donc sa taille diminuer de \(1\). Puis on réitère le processus jusqu’à la fusion complète des deux listes. On obtient alors une liste triée de taille \(n_1+n_2\), où \(n_1\) et \(n_2\) sont respectivement les longueurs des listes \(L_1\) et \(L_2\).
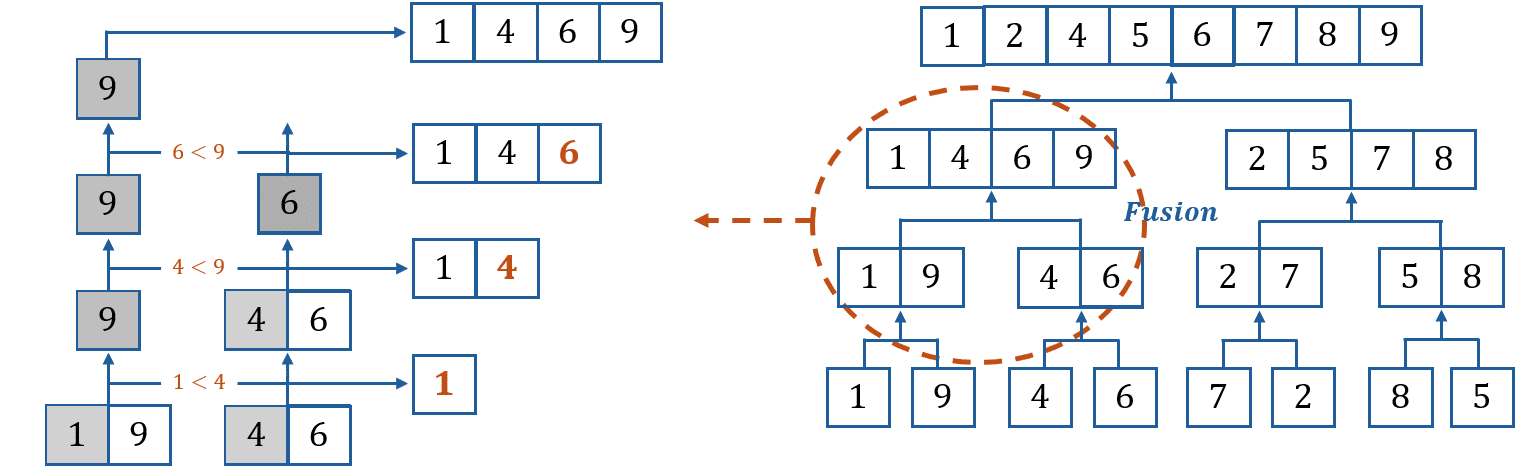
La fusion des listes \([1, 9]\) et \([4, 6]\) est décrite sur le schéma ci-dessus, à gauche. Ainsi, pour chaque étape de la phase de fusion est appliquée une fonction fusion. C’est pourquoi celle-ci s’écrit naturellement de façon récursive.
Le principe du tri fusion étant expliqué, passons dès lors à son implémentation sur Python. Commençons par l’implémentation du script effectuant la fusion. Celui-ci prend en argument deux listes déjà triées pour les fusionner en une seule liste triée.
Les lignes \(2\) et \(3 \) fixent les conditions d’arrêt. Ainsi, si la liste \(A\) correspond à la liste vide, alors il ne reste que la liste \(B\), qui est déjà triée, donc on la renvoie. De façon analogue pour les lignes \(4\) et \(5\).
Les lignes \(6\) et \(7\) assurent le processus de fusion consécutif. En effet, si le premier élément de la liste \(A\) est plus petit que celui de la liste \(B\), alors le premier élément de la liste triée sera le premier élément de la liste \(A\). Ensuite, il nous suffit de réitérer le processus en commençant la fusion à partir de l’indice \(1\) de la liste \(A\), etc. Le processus est similaire pour les lignes \(8\) et \(9\), sauf que cela concerne la liste \(B\).
Le script de fusion étant créé, passons au script du tri :
Remarque
La ligne \(6\) est bien sur une seule ligne :
Les lignes \(3\) et \(4\) fixent le cas d’arrêt. Effectivement, si la liste \(L\) est de longueur inférieure ou égale à \(1\), alors la liste est déjà triée, puisque celle-ci ne possède qu’un seul élément.
Les lignes \(5\) et \(6\) effectuent le processus de division (la descente de tri) et le processus de fusion (la remontée du tri) de façon récursive.
Algorithme de tri rapide
Cet algorithme de tri considère une clé (case grisée), de façon aléatoire – nous considérerons toujours le dernier élément de la liste pour des raisons pédagogiques.
Le principe est le suivant : on crée deux sous-listes. Dans la première, on range les éléments strictement inférieurs à la clé et, dans la seconde, on range les éléments supérieurs à la clé. Pour la suite, il nous suffit de réitérer le procédé pour les deux nouvelles listes créées, en considérant deux nouvelles clés, etc. In fine, il suffira de faire l’addition de toutes ces sous-listes créées, dont il ne restera qu’un seul élément, pour obtenir la liste triée.
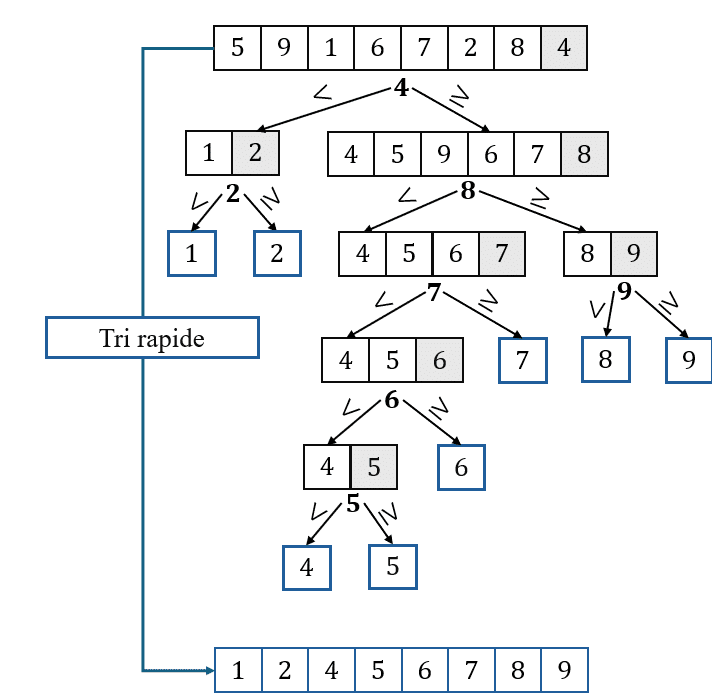
Afin que cela soit plus concret, considérons le tri de la liste \([5,9,1,6,7,2,8,4]\).
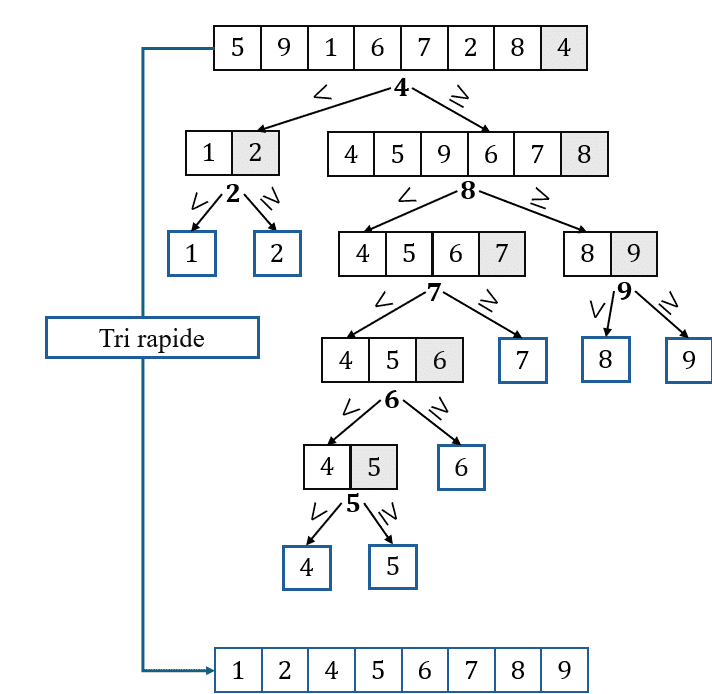
On considère que le dernier élément (c’est-à-dire \(4\)) est la clé de la liste. Ainsi, on crée deux sous-listes dans lesquelles on place à gauche les éléments strictement inférieurs à \(4\) et à droite les éléments supérieurs à \(4\). Cette étape se nomme « étape de partitionnement ». On obtient dès lors les sous-listes respectives suivantes : \([1,2]\) et\([4,5,9,6,7,8]\). Puis on réitère le procédé…
Le principe étant expliqué, passons à l’implémentation de l’algorithme sur Python. Mais avant cela, il nous faut écrire un script qui permette de partitionner la liste selon la clé.
La ligne \(2\) fixe le dernier élément de la liste comme pivot.
La ligne \(3\) considère la variable \(i\) comme le dernier élément plus petit que le pivot. On l’initialise à \(-1\) de sorte que cela corresponde bien au parcours de la liste \(L\).
Les lignes \(5\) à \(7\) permettent de ranger à gauche, les éléments strictement plus petits que le pivot.
La ligne \(8\) positionne le pivot au début de la liste constituée des éléments supérieurs au pivot.
Enfin, la dernière ligne, la ligne \(9\), renvoie l’indice du pivot dans la liste \(L\), indice qui permet le fameux partitionnement.
Cela étant fait, passons à l’implémentation du script de tri rapide :
Les lignes \(2\) et \(3\) constituent le cas d’arrêt de la fonction récursive. En l’occurrence, elle s’arrête lorsque la liste en argument est constituée d’un seul élément.
La ligne \(4\) est le partitionnement de la liste placée en argument.
La ligne \(5\), effectue, à l’aide des appels récursifs, la somme de chaque sous-liste triée.
Remarque
La ligne \(5\) est bien sur une seule ligne :
Conclusion sur les types d’algorithmes de tri
Désormais, tu connais les quatre principaux algorithmes classiques qui peuvent tomber aux concours.
Pour aller un peu plus loin, et mieux appréhender la raison d’existence de chaque algorithme de tri, il serait intéressant de calculer leur complexité temporelle (temps de calcul pour un nombre élevé de données en entrée), afin d’exhiber les forces et les faiblesses de chaque algorithme, les uns par rapport aux autres.
Tu peux retrouver ici le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder ici à toutes nos autres ressources sur Python !