Un algorithme de tri est un processus qui permet d’organiser des données dans un ordre précis (croissant ou décroissant). Chaque méthode a sa propre approche, comme le tri par insertion et le tri rapide. En parallèle, les algorithmes de recherche permettent de localiser efficacement des éléments dans une liste. Bien que ces algorithmes ne fassent pas partie du programme officiel des ECG, ils peuvent tout de même apparaître lors des concours des Parisiennes ainsi que dans les sujets d’oraux de l’ESCP et de HEC. Les maîtriser pourrait donc offrir un avantage stratégique.
Les algorithmes de tri
Le tri par insertion
Le tri par insertion consiste à prendre le premier élément à trier et à l’ajouter au début d’une nouvelle liste. Ensuite, chaque nouvel élément est inséré à sa position appropriée dans la liste déjà triée. Ce processus est répété jusqu’à ce que tous les éléments de la liste initiale soient intégrés.
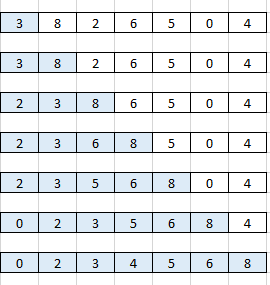
On applique ici l’algorithme du tri par insertion sur la liste [ 3 , 8 , 2 , 6 , 5 , 0 , 4 ] :
Voici un script possible :
Le tri par sélection
Le tri par sélection consiste à identifier la plus petite valeur dans la liste, puis à l’échanger avec l’élément en première position. Ce processus est répété sur la sous-liste des éléments restants jusqu’à ce que tous les éléments soient triés.
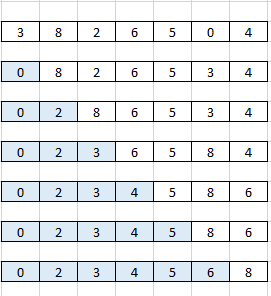
On applique dans cet exemple l’algorithme du tri par sélection sur la liste [ 3 , 8 , 2 , 6 , 5 , 0 , 4 ] :
Voici un script possible :
Le tri à bulles
Le tri à bulles repose sur la comparaison d’éléments adjacents dans une liste, effectuée par paires. À chaque étape, si l’élément e1 est supérieur à l’élément e2, une permutation est effectuée pour les échanger. Ce processus se répète à travers toute la liste jusqu’à ce qu’aucune permutation ne soit plus nécessaire, indiquant ainsi que la liste est triée.
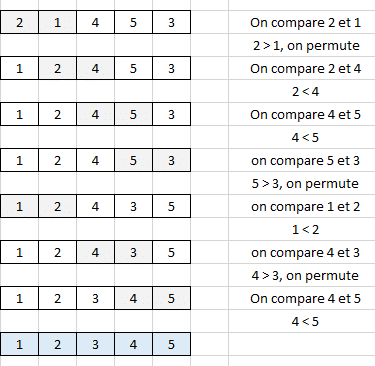
On applique ici l’algorithme du tri à bulles sur la liste [2 , 1 , 4 , 5 , 3]
Voici un script possible :
Remarque : dans les algorithmes précédents, si on change T[j] > T[Pos] par T[j] < T[Pos], l’ordre de tri devient plutôt décroissant que croissant.
Le tri rapide
Avant d’analyser en détail cette méthode, il est important d’avoir quelques connaissances sur le récursif sur Python.
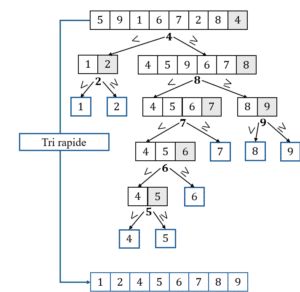
L’algorithme de tri rapide utilise le principe « diviser pour régner ». Il commence par choisir un élément, appelé « pivot », et partitionne la liste en plaçant tous les éléments inférieurs au pivot à sa gauche et ceux qui sont supérieurs à sa droite. Une fois le pivot à sa position finale, l’algorithme s’applique récursivement aux sous-listes de gauche et de droite. Ce processus se répète jusqu’à ce que chaque sous-liste contienne un seul élément ou qu’elle soit vide, aboutissant ainsi à une liste triée.
Voici un script possible :
Les algorithmes de recherche
Recherche d’un élément dans une liste quelconque
En fait, Python dispose déjà de l’opérateur in pour tester si un élément figure dans une liste et de l’opérateur index qui permet de renvoyer l’indice de l’élément dans la liste s’il a été trouvé.
Pour vérifier l’existence d’un élément a, il suffit d’écrire print (a in liste) qui va renvoyer True si l’élément existe dans la liste, ou False sinon. Et pour avoir l’indice de l’élément a, il suffit d’écrire print (liste.index(a)).
Cependant, il est possible de créer nos propres algorithmes.
Pour l’algorithme de recherche, il suffit de parcourir la liste et de retourner True dès que l’élément recherché est trouvé, ou False si l’ensemble de la liste a été parcouru sans le trouver.
Voici un script possible :
On peut également proposer une version qui retourne l’indice de la première occurrence de l’élément recherché s’il est trouvé.
Recherche d’un élément dans une liste triée
Lorsqu’une liste est triée par ordre croissant, on peut considérablement optimiser nos algorithmes en appliquant le principe de la recherche dichotomique (même principe pour approcher la solution d’équation f(x)=0).
- On commence par identifier l’élément central de la liste. Si cet élément correspond à celui recherché, l’algorithme s’arrête. Dans le cas contraire, une comparaison est effectuée.
- Si l’élément recherché est inférieur à l’élément central, la recherche se poursuit dans la première moitié de la liste. Sinon, elle se fait dans la seconde moitié.
- On répète ensuite ces étapes en appliquant l’algorithme à l’une des deux sous-listes.
Voici un script possible :
On peut également proposer une version qui retourne l’indice de la première occurrence de l’élément recherché dans le cas d’une liste triée.
Voici un script possible :
Remarque : en Python, les listes sont indexées à partir de 0. Cela signifie que le premier élément d’une liste se trouve à l’indice 0, et non pas à l’indice 1, comme on pourrait l’attendre dans des contextes mathématiques.
Recherche du maximum ou du minimum d’une liste
Pour trouver le maximum et le minimum d’une liste, Python dispose déjà de deux fonctions min et max pour effectuer cette tâche. On peut également proposer notre propre algorithme. Il s’agit simplement de parcourir les éléments de la liste un par un, en comparant chaque élément avec le minimum ou le maximum trouvé parmi les éléments précédents.
Voici un script possible :
Conclusion
Les algorithmes de tri et de recherche jouent un rôle crucial dans l’organisation efficace des données et la localisation d’éléments. Chacun d’eux possède des caractéristiques distinctes et des méthodes de fonctionnement adaptées à diverses situations. Maîtriser ces algorithmes peut constituer un atout précieux le jour J. D’ailleurs, le sujet des algorithmes de tri est déjà tombé aux épreuves écrites dans le sujet Math 2 HEC 2024.