Les fonctions de n-variables représentent un des chapitres les plus redoutés par les étudiants d’ECG. C’est pourquoi être à l’aise avec la programmation Python relative à ce chapitre peut permettre de se démarquer au concours. Dans cet article, il sera question de tout ce que tu dois connaître d’essentiel pour maîtriser la programmation Python des fonctions de n-variables pour briller le jour J.
Introduction
Nous allons évoquer de manière générale des fonctions de n-variables, mais nous nous concentrerons également sur les fonctions de deux variables. En effet, ce sont les fonctions qui tombent le plus souvent au concours et, surtout, ce sont les seules qui permettent d’obtenir une représentation graphique en Python.
Dans cet article, il sera notamment question de gradient, de dérivées partielles, de plan tangent. Fais en sorte que ces notions soient claires pour toi afin d’être plus à l’aise sur ce qui va suivre. Pour toutes ces notions, nous utiliserons \(f(x,y) = x^2-y^2\), qui est tombée dans le sujet EDHEC 2024 en mathématiques approfondies.
Librairies
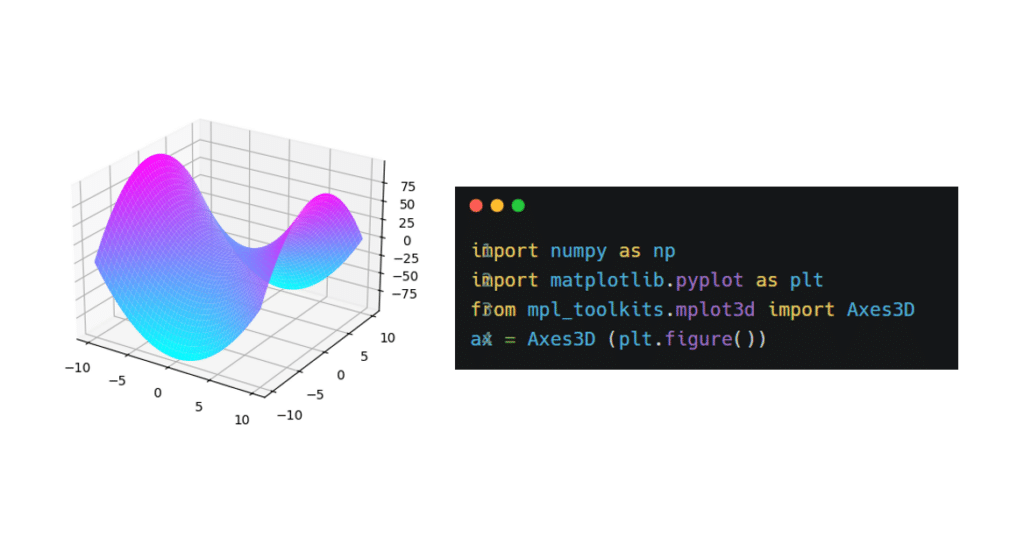
Afin de pouvoir travailler sur la représentation graphique des fonctions de deux variables en Python, il est nécessaire d’importer des librairies. Ainsi, il sera toujours nécessaire de faire précéder son script des lignes suivantes.
La première est utile pour les vecteurs, la deuxième pour les représentations graphiques, tandis que les deux dernières sont spécifiques à la représentation graphique en 3D.
Cas des fonctions de n-variables
Tu verras très rapidement que ce cas est très limité en Python et c’est pourquoi nous nous restreindrons très vite au cas des fonctions de deux variables.
Pour ce que nous verrons dans le cas général de ces fonctions, il n’est d’ailleurs pas nécessaire d’importer les librairies précédentes.
Dans le cas général, il est possible de créer un programme permettant de calculer les images d’une telle fonction. Un exemple vaut mieux que mille mots : voici un programme qui permet de calculer les valeurs de \( f: (x_0,…x_4) \mapsto\left(\displaystyle \sum_{k=0}^{4}x_k^2\right) – 4\left(\displaystyle \sum_{k=0}^{4}x_k\right)\)
Ici, l’utilisation d’un vecteur apparaît pertinente pour simplifier les calculs.
Cas des fonctions de deux variables
Pour rappel, ce qui a été vu dans le cas des fonctions de n-variables reste vrai dans le cas des fonctions de deux variables. Dans ce cas, nous pourrons aller vraiment plus loin avec une étude graphique des fonctions.
Graphe de \(f\)
Voici les étapes pour définir le graphe d’une fonction \(f\) à deux variables :
On définit la fonction f, comme vu dans le paragraphe précédent. Puis, on crée deux vecteurs x et y subdivisant les intervalles \([a;b]\) et \([c;d]\) selon n points de référence régulièrement espacés via les commandes x = np.linspace(a ,b ,n) et y = np.linspace (c ,d ,n). Ensuite, on représente le maillage (cf. capture d’écran de la fonction ci-dessous) avec la commande X ,Y = np.meshgrid (x ,y). Enfin, on réalise le tracé de \(f\), puis on l’affiche avec les commandes ax.plot_surface(X ,Y ,f(X ,Y )) et plt.show ().
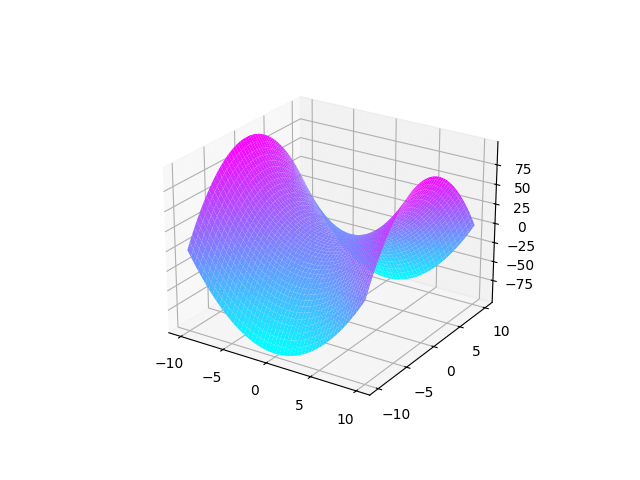
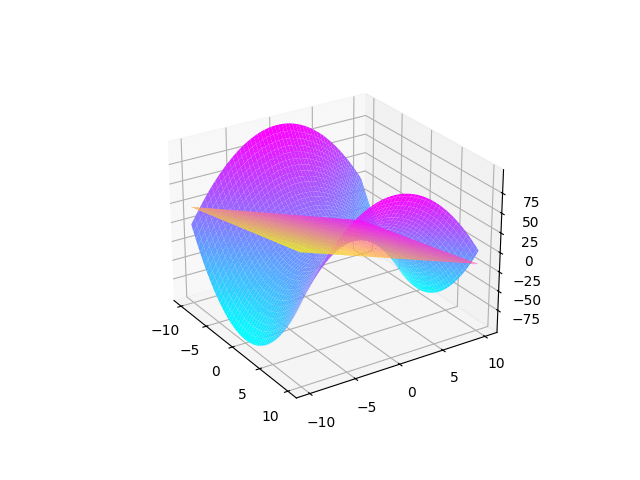
Exemple : traçons le graphe de la fonction \( f: (x,y) \mapsto x^2-y^2\)sur\( [-10,10]^2\)
Bonus : tu peux modifier la couleur de ton graphe. C’est ce qui est fait dans le script en rajoutant « cmap =’cool’ ». Tu peux tester d’autres couleurs en remplaçant cool par winter, spring, summer ou encore hot.
Lignes de niveau
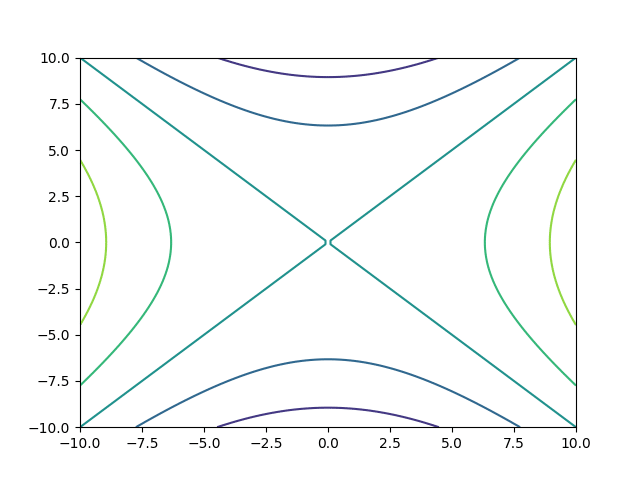
Il est également possible en Python d’obtenir les lignes de niveau d’une fonction avec la commande plt.contour (X,Y, f(X,Y), N), où N est un entier de telle sorte que l’on obtienne N-1 lignes de niveau réparties uniformément entre les valeurs minimales et maximales de f. On peut également remplacer N par un vecteur qui contient directement les valeurs des lignes de niveau voulues. Attention, n’oublie pas de supprimer la ligne ax = Axes3D (plt.figure()) pour obtenir un rendu en deux dimensions comme souhaité. Restons avec l’exemple de notre fonction f précédente et plaçons-nous dans le cas N=5 :
Dérivées partielles et gradient
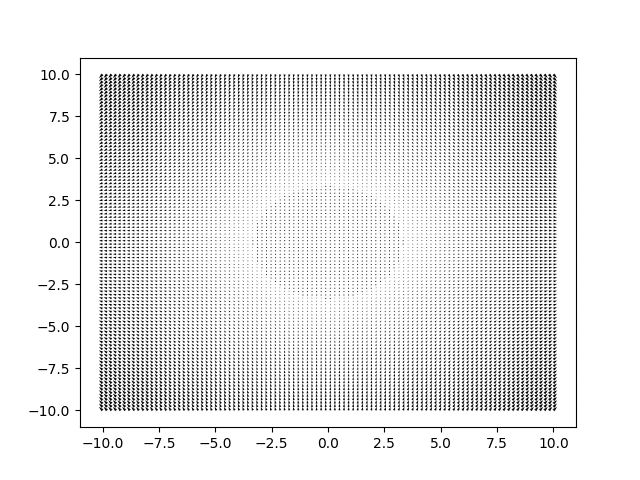
Pour obtenir un champ de gradient, il convient tout d’abord de savoir déterminer à la main les deux dérivées partielles de f. En effet, nous allons ici nous servir de l’instruction plt.quiver (X ,Y , d1f (X ,Y ), d2f (X , Y )), où d1f est la première dérivée partielle de f et d2f est la deuxième.
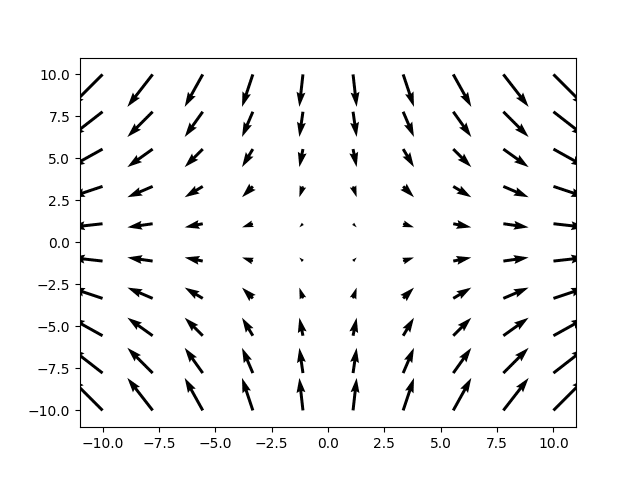
Pense à garder la ligne ax = Axes3D (plt.figure()) désactivée, puisque nous cherchons encore ici un rendu en deux dimensions ! Un exemple restera toujours plus parlant : une fois que tu as déterminé les deux dérivées partielles de \(f(x,y) = x^2-y^2\), il ne te reste plus qu’à écrire le code que voici :
Attention, il faut faire attention au nombre de flèches que l’on veut obtenir. Pour cela, je te conseille de modifier la valeur de tes lignes 5 et 6 en baissant la dernière valeur dans np.linspace. Par exemple, nous sommes ici passés de 100 à 10. Si tu ne le fais pas, tu obtiendras le résultat suivant, qui est tout de suite moins convaincant.
Plan tangent
Voilà le dernier point à connaître absolument sur la représentation graphique des fonctions de n-variables en Python. Si tu connais parfaitement la définition du plan tangent au voisinage du point \((x_0,y_0)\), alors il y a simplement à afficher le graphe de \(f\) ainsi que celui de la fonction affine correspondant au plan tangent. Par exemple, si on reste dans notre exemple avec le plan tangent de \(f\) au voisinage du point \((1,2)\), voici le code et la représentation graphique que l’on obtient :
Conclusion
En définitive, le Python sur les fonctions de n-variables nécessite avant tout une bonne connaissance du cours. Toutefois, les sujets qui y font appel ne vont pas trop loin dans les notions abordées, sachant peut-être que la plupart des étudiants ne sont pas à l’aise avec ce chapitre en Python. À titre d’exemple, tu peux regarder l’exercice 1 du sujet EDHEC 2024. Maintenant, il n’y a plus qu’à croiser les doigts pour toi en espérant que cette notion tombe aux concours.
Tu peux retrouver ici le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder ici à toutes nos autres ressources mathématiques !