Nous allons explorer les méthodes d’interpolations polynomiales appliquées à Python qui possèdent des fonctions intégrées dans certaines bibliothèques afin de simuler certains types d’interpolations. Nous reviendrons très rapidement sur les définitions et les objectifs de ces méthodes pour te rafraîchir la mémoire et que tu comprennes les scripts Python plus aisément. En revanche, nous n’explorerons pas les fondements et les propriétés purement mathématiques des méthodes.
Pour rappel, l’interpolation polynomiale construit un polynôme unique \(P_n(x)\) de degré au plus \(n\) passant par \(n+1\) points distincts \((x_i, y_i)\). Nous développerons dans cet article l’interpolation de Lagrange et la méthode de Newton.
Rappels mathématiques
La méthode de Lagrange
Elle exprime le polynôme comme une somme pondérée des ordonnées \(y_i\), utilisant les polynômes de base de Lagrange \(L_i(x)\).
\[
P_n(x) = \sum_{i=0}^{n} y_i L_i(x) \quad \text{avec} \quad L_i(x) = \prod_{j=0, j \ne i}^{n} \frac{x – x_j}{x_i – x_j}
\]
Pour autant, l’inconvénient principal est la lourdeur du recalcul de tous les \(L_i(x)\) si un point est ajouté, contrairement à la seconde méthode que voici.
La méthode de Newton
Elle est privilégiée en calcul numérique, car elle est itérative et permet un ajout facile de points.
Elle s’exprime comme :
\[
P_n(x) = c_0 + c_1(x-x_0) + c_2(x-x_0)(x-x_1) + \ldots + c_n \prod_{i=0}^{n-1} (x-x_i)
\]
Pour mémoire, les coefficients \(c_k\) sont appelés différences divisées et l’enjeu est justement le calcul de ces coefficients. Nous ne reviendrons pas dessus, assure-toi d’avoir quelques bases avec cette méthode.
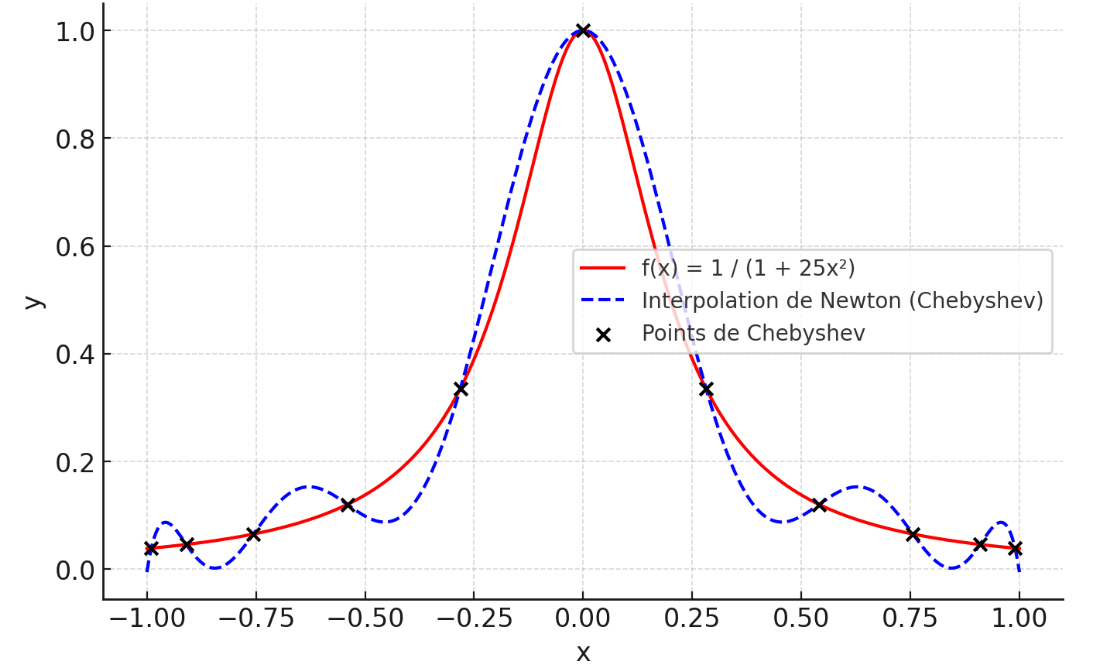
La principale faiblesse de ces méthodes est appelée phénomène de Runge : des oscillations non désirées se produisent aux extrémités de l’intervalle lorsque les points d’interpolation sont équidistants et que le degré \(n\) du polynôme interpolateur est élevé.
Ainsi, il faut choisir des points qui se densifient aux extrémités, ces derniers sont appelés points de Tchebychev.
Pour l’intervalle \([-1, 1]\), les points de Tchebychev sont donnés par :
\[
x_k = \cos \left( \frac{2k + 1}{2n + 2} \pi \right)
\]
Implémentation pratique en Python
Script : interpolation de Lagrange
En pratique, on utilise ‘scipy.interpolate.lagrange’ pour obtenir le polynôme unique et on assure la stabilité en choisissant les points de Tchebychev, comme on a pu le voir dans les rappels de la première partie de cet article.
Ce script est assez long, mais peut être facilement décortiqué.
On crée d’abord la fonction que l’on aimerait interpoler (ici notée \(f\)). Il faut ensuite générer les abscisses des points d’interpolation de Tchebychev (ces fameuses abscisses optimales).
On a ici choisi arbitrairement un polynôme interpolateur de degré 10 et, après avoir trouvé les abscisses optimales, on calcule leurs images respectives (on manipule ici des vecteurs). La fonction ‘lagrange’ permet de conclure la fonction en calculant directement le polynôme interpolateur pour de tels points.
La fonction ‘P_tcheb.c’ permet de ne renvoyer que la liste des coefficients du polynôme obtenu.
Voici ce que l’on obtiendrait en exécutant ce code :
Comme les termes impairs sont très largement négligeables (car proches de 0), on pourrait ainsi considérer le polynôme suivant :
\[
P(x) \approx 1.0x^{10}
– 12.4765x^{8}
+ 61.4430x^{6}
– 133.4448x^{4}
+ 130.1058x^{2}
– 46.6329
\]
Script : interpolation de Newton
L’algorithme des différences divisées vise à obtenir les coefficients \(c_k\). Attention, le code est long, mais il n’est pas pour autant difficile à appréhender.
Comme dans le script précédent, on prend une fonction \(f\) que l’on cherche à interpoler et on génère ensuite les points de Tchebychev afin de choisir les points d’interpolation optimaux pour obtenir un polynôme aussi précis que possible.
La spécificité de ce code arrive maintenant, puisqu’on calcule entre les lignes 19 et 24 le vecteur des coefficients des polynômes grâce à la formule qui permet de les obtenir (sur laquelle nous ne sommes pas revenus dans la première partie de cet article).
Une fois cela réalisé, on a passé le plus technique. On a ici choisi arbitrairement un polynôme de degré 10. On calcule ensuite les ordonnées \(y\) à l’aide de la fonction \(f\) et des abscisses \(x\) optimales. La ligne 30 applique ensuite la fonction qui permet d’obtenir les coefficients du polynôme aux points optimaux afin d’obtenir le polynôme final.
Libre à toi par la suite de modéliser un résultat graphique du polynôme interpolateur et de notre fonction qu’on a cherchée à interpoler. Voici le résultat que cela donnerait pour le script précédent. Plutôt satisfaisant, non ?
Conclusion
En définitive, les deux méthodes d’interpolation sont assez différentes, mais permettent d’obtenir un résultat similaire. Si tu ne devais retenir qu’une seule des deux méthodes, je te conseille de travailler en priorité l’interpolation de Lagrange qui retombe bien plus souvent dans les sujets d’écrits et d’oraux. La seconde méthode reste toutefois pertinente et pourrait très bien faire l’objet d’un sujet d’écrit de type Parisiennes.
Tu peux retrouver ici le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder ici à toutes nos autres ressources mathématiques !