En arithmétique, les nombres premiers sont incontournables. Au-delà de leur simplicité apparente, les raisonnements qui se cachent derrière ces derniers sont très intéressants sur Python. Ainsi, dans cet article, nous allons voir comment on peut implémenter des programmes classiques autour de cette notion. Tu vas ainsi découvrir des programmes qui permettent de déterminer si un nombre est premier ou non, de trouver un grand nombre de nombres premiers, etc. Bien que ces programmes ne soient pas exigibles le jour du concours, les commandes et les méthodes utilisées, elles, le sont en général !
Rappel de la définition d’un nombre premier
Avant de rentrer dans le vif du sujet, un petit rappel sur les nombres premiers et les notions qui les entourent ne fait pas de mal.
Tout d’abord, \(a\) est un diviseur de \(b\) si, et seulement si, le reste de la division euclidienne de \(b\) par \(a\) est nul. Ainsi, \(3\) est un diviseur de \(9\), car \(9 = 3 \times 3 + 0.\) En revanche, \(3\) n’est pas un diviseur de \(10\), car \(10 = 3 \times 3 + 1.\)
Ensuite, un nombre premier est un entier naturel qui n’admet que deux diviseurs entiers et positifs, différents l’un de l’autre : lui-même et \(1\). Par conséquent, \(1\) n’est pas un nombre premier, car bien qu’il soit divisible par lui-même et par \(1\), les deux diviseurs sont identiques (\(=1\)), donc \(1\) ne correspond pas à la définition d’un nombre premier. Ainsi, le plus petit nombre premier est \(2\), car parmi les entiers naturels, seuls \(1\) et \(2\) sont des diviseurs de \(2\).
Voilà, on peut enfin s’attaquer aux programmes Python !
Le crible d’Ératosthène
Explication du crible
Grâce à ce premier programme, nous allons pouvoir déterminer un nombre considérable de nombres premiers.
Pour ce faire, nous allons utiliser le crible d’Ératosthène. Cette méthode consiste à prendre \(n\) entiers naturels consécutifs partant de 2, puis à barrer tous les multiples de 2. Ensuite, on garde l’entier naturel le plus proche de 2 qui n’a pas été barré, en l’occurrence 3, puis on barre également tous ses multiples. Une fois de plus, on garde l’entier naturel le plus proche de 3 qui n’a pas été barré (5) et on réitère ainsi de suite le procédé, jusqu’à ne plus pouvoir garder un nouveau nombre.
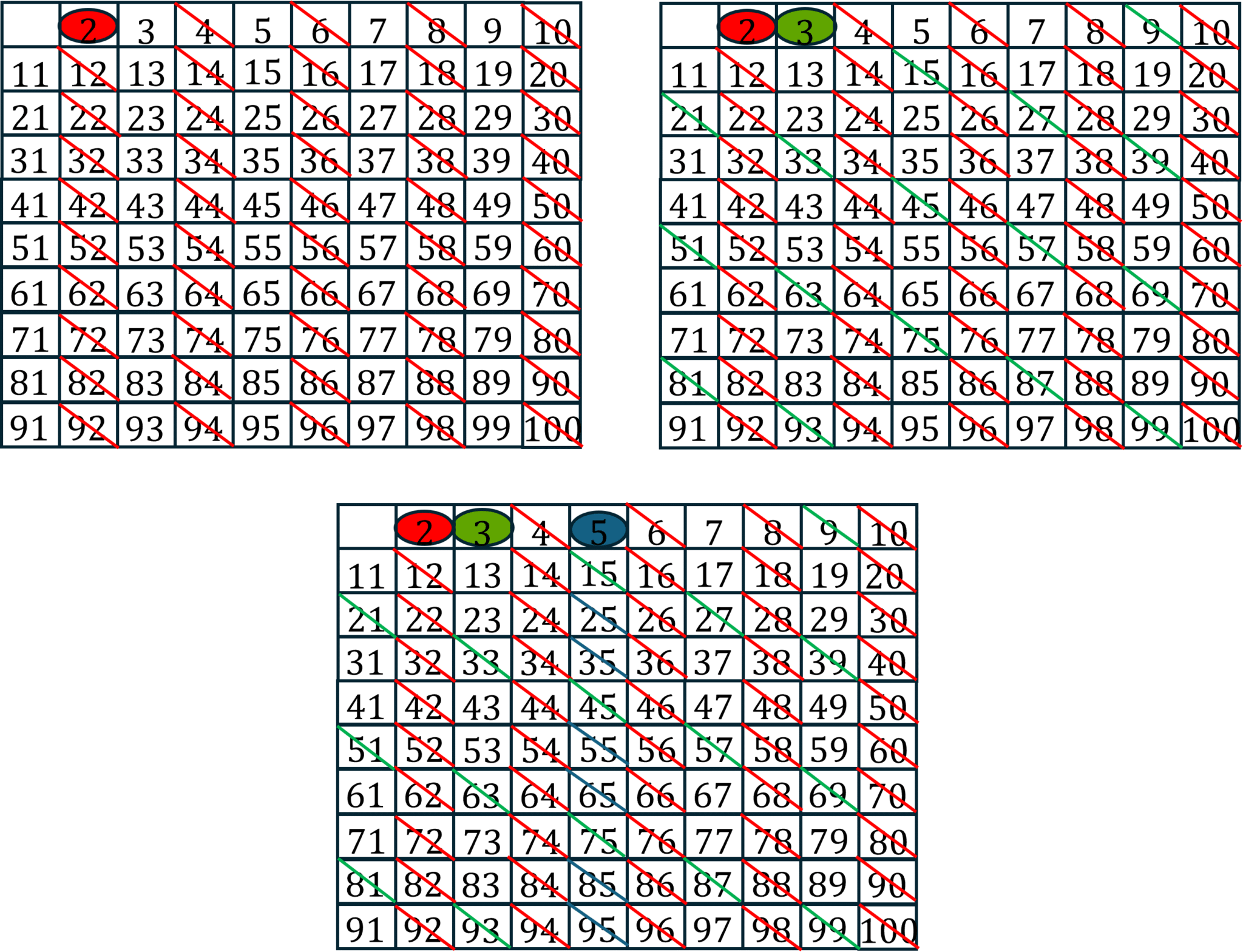
Maintenant qu’on a vu le procédé mathématique, regardons maintenant comment retranscrire cet algorithme sur Python.
Application du crible sur Python
Voici un programme qui met en œuvre le crible d’Ératosthène :
Les prochaines lignes visent à expliquer comment ce programme fonctionne
Le programme se divise en deux parties :
- La première partie, qui va de la ligne 4 à la ligne 10, vise à appliquer le crible, à une différence près : au lieu de « barrer » les multiples des nombres premiers, on les remplace par des 0.
- La deuxième partie, qui va de la ligne 11 à la ligne 17, a pour objectif de retirer tous les 0 de la liste, afin de retourner, à la fin du programme, une liste avec que des nombres premiers allant jusqu’à \(n\), avec en supplément le nombre de nombres premiers trouvés.
Si on rentre plus dans les détails :
La ligne 5 crée une liste avec tous les entiers allant de 0 à \(n\).
La ligne 6 remplace le 1 de la liste créée précédemment par un 0.
Pour la ligne 7, on fait arrêter i à la valeur \(\sqrt{n}\) (en partie entière), pour simplifier le programme : on pourrait le faire aller jusqu’à n, mais on sait que si \( n = a \times b\)(\(a\) et \(b\) deux entiers naturels), avec \(b\le a\), alors \(b \le \sqrt{n}\), car \(\sqrt{n} \times \sqrt{n} = n\). Ainsi, lorsque i s’arrête à la valeur \(\sqrt{n}\), on est sûrs d’avoir retiré tous les multiples de nombres premiers présents dans notre grille d’entiers naturels. Par exemple, pour \(n = 100\) ( avec donc \(\sqrt{n}=10 \)), \(71\) est un nombre premier inclus dans la liste. Si \(71\) s’écrivait sous la forme \(a \times b\) (les deux étant des entiers naturels), avec \(b\le a\), alors \(b\) serait inférieur à \(\sqrt{71} \le 9 \le \sqrt{n} = 10\), donc l’algorithme l’aurait détecté.
Dans la ligne 9, floor(n/i) nous garantit de brasser tous les multiples présents dans la liste d’un nombre i donné.
Dans la ligne 12, la commande len(L) renvoie le nombre d’éléments dans L.
La commande .remove(a) présente dans la ligne 14 permet de retirer la première occurrence du nombre a présent dans la liste.
La ligne 16 est équivalente à a = a + 1.
Maintenant qu’on a vu comment trouver des nombres premiers, voyons ensuite comment créer un algorithme qui nous permet de savoir si un entier naturel quelconque est un nombre premier ou non.
Déterminer si un nombre donné est premier ou non
Dans le programme suivant, on rentre un nombre entier positif et le programme nous ressort un booléen (True et False) qui indique si le nombre rentré est bien un nombre premier ou pas.
La ligne 5 applique la même méthode que celle qui a été appliquée dans le programme précédent.
Dans la ligne 6, l’opérateur % donne le reste de la division euclidienne de \(n\) par \(k\). Ainsi, si \(n\) est divisible par\(k\), alors \(n\) % \(k = 0\).
Si, malheureusement, le nombre entré n’est pas un nombre premier, on peut s’amuser à coder un programme qui nous donne la décomposition en nombres premiers de ce dernier. C’est le prochain programme que nous allons voir.
La décomposition en produit de facteurs premiers
Voici un programme qui, pour un entier naturel donné \(n\), donne sa décomposition en facteur de nombres premiers sous la forme d’une liste :
Quelques petites explications s’imposent.
Le programme regarde si le nombre \(n\) est divisible par 2, puis regarde s’il est divisible par des nombres impairs, même s’ils ne sont pas des nombres premiers (cela ne pose pas de problème, car les nombres impairs qui ne sont pas premiers ont des diviseurs impairs qui eux sont premiers ; par exemple, 9 est déjà divisible par 3). À chaque fois que \(n\) est divisible par un nombre \(k\), on l’ajoute dans la liste et on remplace la valeur de \(n\) par \( \displaystyle \frac{n}
{k}\).
La ligne 4 s’appuie sur la méthode vue précédemment.
Dans la ligne 6, la commande .append(a) permet d’ajouter l’élément a dans la liste.
La ligne 10 ajoute la valeur de n qui correspond, à ce moment du programme, à un nombre premier dont la racine est plus petite que a (essaye avec \(n\) = 12 par exemple).
Conclusion
Te voilà désormais dans de bonnes conditions pour affronter sans peur et sans reproche les programmes Python classiques autour des nombres premiers.
Tu peux retrouver ici le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder ici à toutes nos autres ressources sur Python !