Un algorithme récursif est un algorithme qui s’appelle lui-même, jusqu’à atteindre une condition d’arrêt (ou condition de terminaison), c’est-à-dire une ou plusieurs conditions où la fonction renvoie une valeur sans appel à elle-même. L’existence et le choix de la condition d’arrêt sont primordiaux, sans quoi l’algorithme continuerait les appels sans jamais s’arrêter, ce qui serait malheureux pour ton ordinateur…
Quelques remarques préliminaires
Bien que ces algorithmes fassent souvent peur de prime abord, ils permettent la résolution de certains problèmes de façon intuitive.
Très souvent, les algorithmes récursifs sont introduits à la lumière des algorithmes dits « itératifs ». En effet, les algorithmes itératifs utilisent des boucles while et for pour répéter des opérations, alors que les algorithmes récursifs ont la particularité d’utiliser la méthode du « diviser pour régner » en scindant un problème en des sous-problèmes, eux-mêmes scindés en des problèmes plus simples à résoudre, etc.
Structure formelle des fonctions récursives
Un algorithme récursif est composé pour l’essentiel d’un ou plusieurs cas d’arrêt et d’une structure qui fait appel à elle-même :
Deux exemples incontournables des algorithmes récursifs
Implémentation de la fonction factorielle
Pour rappel, la fonction factorielle est définie ainsi : \(\forall n \in \mathbb{N}, \text{ }n! = 1\times2\times…\times n \)
Implémentons cette fonction de façon itérative, on peut considérer le script suivant :
Les lignes 2 et 3 considèrent la convention usuelle suivante : \(0! = 1\) ; la boucle for itère la fonction factorielle. En réalité, il est bien plus intuitif d’écrire la fonction factorielle de façon récursive. En effet, par exemple, pour calculer \(4!\), il nous faut la valeur de \(3!\) et pour \(3!\), il nous faut la valeur de \(2!\).
C’est pourquoi nous allons traduire le script itératif en script récursif. Mais pour cela, nous devons travailler avec une autre définition de la factorielle, c’est-à-dire une définition par récurrence :
\[n! = \begin{cases} 1 & \text{ si } n=0 \\ n\times(n-1)! & \text{si } n\in\mathbb{N}^* \end{cases}\]
Les lignes 2 et 3 décrivent les cas d’arrêt, les cas qui permettent l’arrêt du script. Enfin, les lignes 4 et 5 décrivent le fameux appel récursif. Tu trouveras plus de détails sur le fonctionnement de ce script dans la suite de l’article (partie Arbre d’appel).
On devra très souvent passer par une définition par récurrence pour traduire le script itératif en script récursif.
Implémentation de la suite de Fibonacci
Pour rappel, la suite de Fibonacci est la suite \((F_n)_{n\in\mathbb{N}}\) telle que :
\(
\begin{cases}
F_0=0 \\
F_1=1 \\
\forall n \geq2, F_n=F_{n-1}+F_{n-2}
\end{cases}
\)
De façon analogue à la fonction factorielle, les lignes 2 et 3 sont les conditions de terminaison. Puis, les lignes 4 et 5 sont la structure récursive. Notons que pour la suite de Fibonacci, ou pour les suites en général, il est très intuitif de coder une suite sur Python de façon récursive étant donné que le n-ième élément de la suite dépend des précédents.
Ainsi : \(Fib(6)\) renvoie \(8\).
Bien que ces fonctions s’écrivent intuitivement de façon récursive, il est difficile d’appréhender le fonctionnement de notre script de prime abord. C’est pourquoi nous allons aborder la notion d’arbre d’appel.
Arbre d’appel
En informatique, il est toujours bon de travailler d’abord sur papier avant de coder quoi que ce soit, afin de mieux comprendre ce que l’on écrit et de mieux déceler les rouages de notre script. Ce qui est d’autant plus pertinent que l’informatique, en ECG, est évaluée sur feuille. À cet égard, les algorithmes récursifs n’échappent pas à cette règle, et l’arbre d’appel est une façon simple de se représenter comment les appels sont effectués.
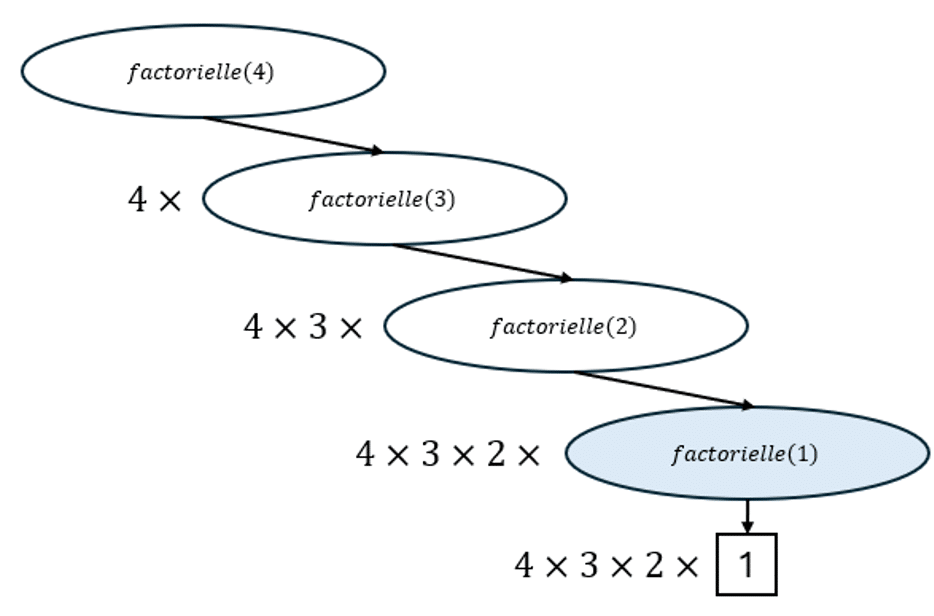
Par exemple, l’arbre d’appel pour la fonction factorielle est le suivant :
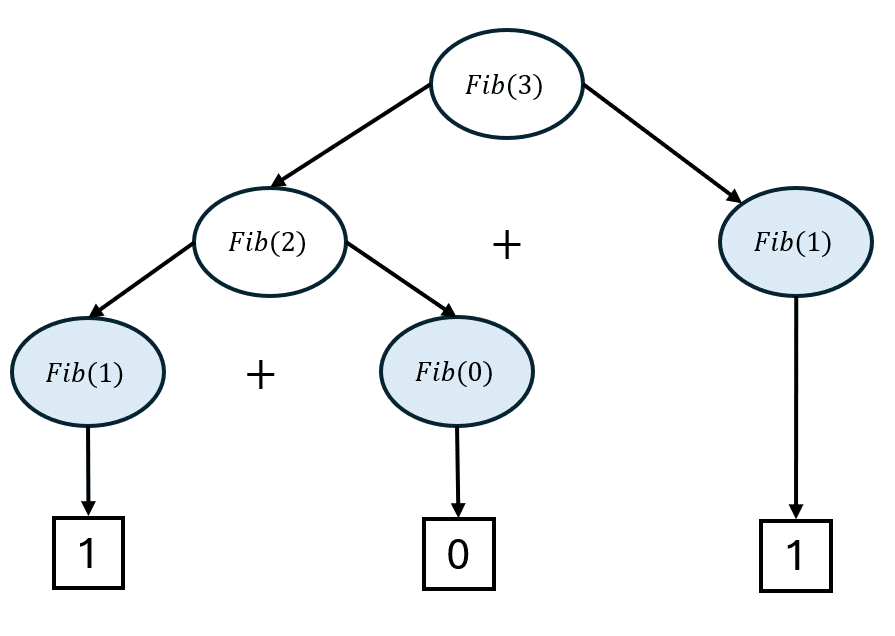
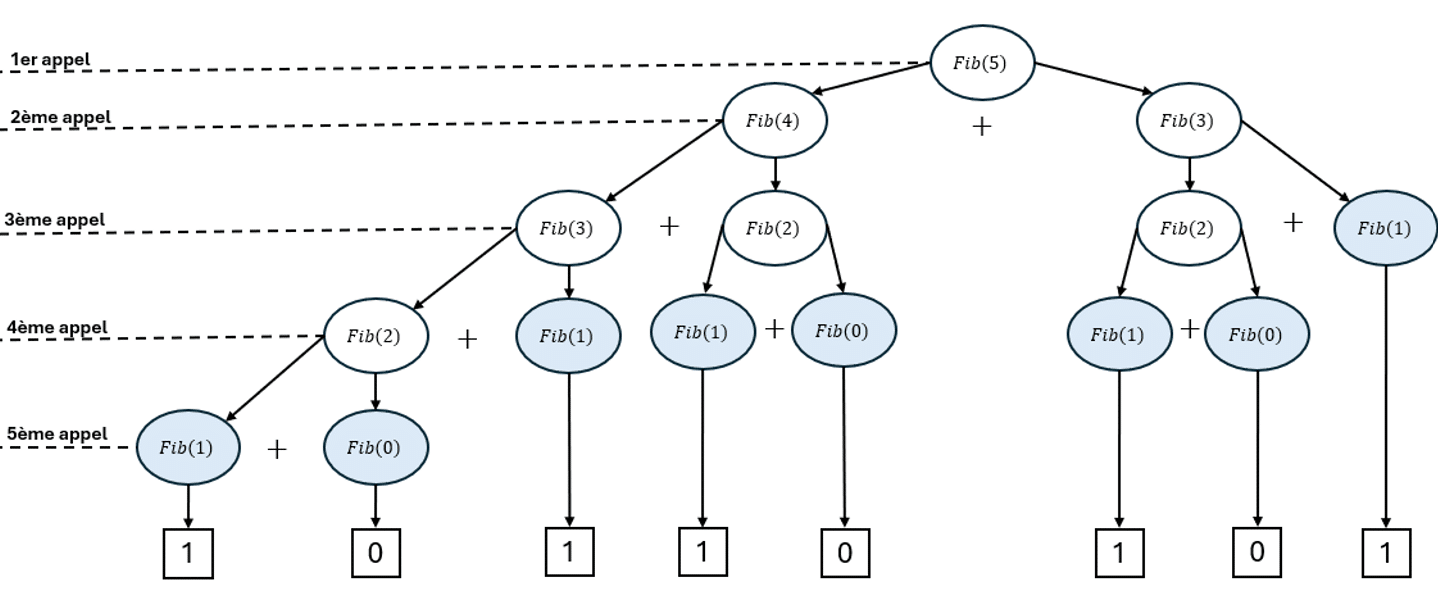
Arbre d’appel pour \(Fib(5)\) est :
Où on a colorié en bleu clair les cas d’arrêt, et où les flèches signifient « fait appel à ».
Ainsi, pour le cas de la suite de Fibonacci, il suffit de faire l’addition des valeurs représentées dans les carrés pour obtenir la valeur de \(Fib(5)\), soit \(5\).
Cette visualisation te permet ainsi une représentation concrète du fonctionnement de ton algorithme récursif, en plus de remarquer une redondance dans les calculs effectués. En effet, on peut ainsi noter que certaines valeurs sont calculées plusieurs fois : \(Fib(2)\) a été calculée \(3\) fois, ou encore \(Fib(1)\) a été calculée à \(5\) reprises. Cette redondance augmente inutilement et considérablement le temps de calcul, c’est-à-dire la complexité de l’algorithme.
Pour que tu puisses être convaincu(e), je te propose de recopier le script récursif et de calculer \(Fib(33)\). Tu as pu alors constater que tu as dû attendre plusieurs secondes (temps qui varie selon la puissance de calcul de ton ordinateur, de ses composants et du compilateur utilisé) avant d’obtenir un résultat, en l’occurrence \(Fib(33)\) renvoie : \(3524578\).
Conclusion sur le récursif sur Python
Ainsi, tu as pu observer que les algorithmes récursifs, un grand classique en informatique, sont moins compliqués qu’ils n’en ont l’air, tant leur écriture est naturelle dans certains cas. Toutefois, tu as pu remarquer quelques limites à ces algorithmes, notamment la redondance des quantités calculées, qui peut avoir des répercussions sur le temps de calcul pour un grand nombre de données. C’est pourquoi les algorithmes récursifs sont assez souvent optimisés à l’aide de la programmation dynamique.
Tu peux retrouver ici le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder ici à toutes nos autres ressources sur Python !